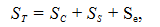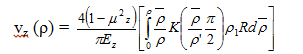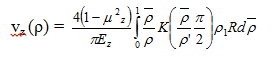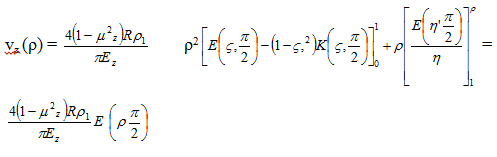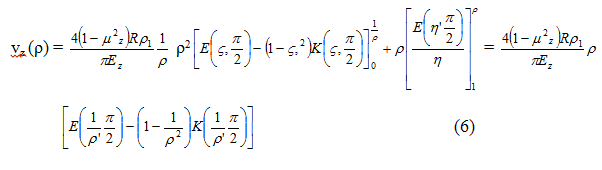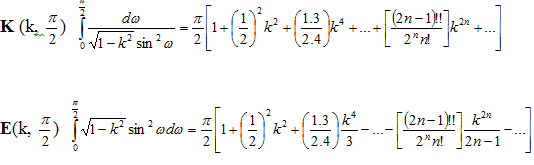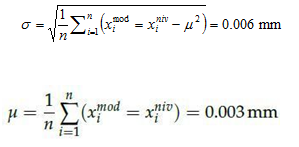Назад в библиотеку
ДЕФОРМАЦИЯ ПОВЕРХНОСТИ ЗЕМЛИ В РЕЗУЛЬТАТЕ ВОЗДЕЙСТВИЯ НАГРУЗКИ ОТ МАССЫ И СНЯТИЯ НАГРУЗКИ
OF TALL BUILDING
Марсель Мойзе, Павол Коллар , Милос Валк
Технологический университет Словакии, Братислава. Западно- Богемский университет, Пилзен.
e-mail: marcel.mojzes@stuba.sk milos.valko@wbupl.cz
Аннотация.
Масса здания вызывает деформацию поверхности земли на значительном расстоянии от места самого здания. Во многих научных работах рассматриваются разнообразные методы моделирования упругого и реологического воздействия осадки. Более глубокое знание механических свойств материалов и современное компьютерное оборудование позволяют создать очень точную модель реагирования поверхности земли на воздействие нагрузки с течением времени. Геодезистам и геофизикам необходимо знать законы деформации и их изменения во времени для разработки опорной геодезической сети и для анализа многократных контрольных измерений горизонтальных и вертикальных временных рядов. В работе представлена математическая модель упругой поверхностной деформации земли в результате воздействия нагрузки от массы и снятия нагрузки.
Ключевые слова:
нагрузка от массы, сжимаемость грунта, упругая осадка земной поверхности.
1. Введение
Увеличение напряжений, вызванное сооружением зданий или другой нагрузкой, сжимает почвенные слои. Сжатие происходит из-за (а) деформации частиц почвы, (б) перемещения частиц почвы и (в) выпаривания воды и вытеснения воздуха из свободных объемов (пустот). В целом, осадка грунта под воздействием нагрузки может быть трех общих видов (Das, 2010):
1. Упругая осадка, вызываемая упругой деформацией сухого грунта, влажного и насыщенного грунта без каких-либо изменений в содержании влажности. Расчеты упругой осадки основываются, как правило, на уравнениях, выведенных из теории упругости.
2. Первичная консолидационная осадка, являющаяся результатом изменений объема насыщенного связного грунта из-за испарения воды находящейся в пустотах.
3. Вторичная консолидационная осадка, наблюдаемая в насыщенных связных грунтах, является результатом приспосабливания структуры грунта вследствие пластической деформации. Она является дополнительной формой компрессии, которая происходит при постоянном эффективном давлении.
В этой работе представлены основные принципы оценки упругой и консолидационной осадки почвенных слоев под воздействием прилагаемой нагрузки.
Общая осадка земной поверхности может быть представлена как
В этой работе представлены основные принципы оценки упругой и консолидационной осадки почвенных слоев под воздействием прилагаемой нагрузки.
Общая осадка земной поверхности может быть представлена как
где ST - общая осадка, Sc - первичная консолидационная осадка, Ss - вторичная консолидационная осадка, Se - упругая осадка.
Когда здания возводятся на суглинках, дающих значительную осадку, консолидационная осадка может быть в несколько раз выше упругой осадки.
2. Упругая осадка
Упругая, или начальная осадка фундамента зданий (Se) происходит непосредственно после приложения нагрузки без изменения содержания влаги в грунте. Величина сдвиговой осадки зависит от податливости здания и типа материала, на котором оно возводится.
В работе (Коллар и др., 2010) уравнение для определения увеличения нагрузки (которая приводит к упругой осадке) вследствие применения кольцевой нагрузки рассчитывалось с учетом следующих предположений:
• Нагрузка прилагается на поверхности земли.
• Нагружаемая площадь податливая.
• Почвенная среда однородная, упругая, изотропная и простирается на значительную глубину.
2.1. Кольцевая нагрузка
Давайте начнем с рассмотрения границ поверхности деформации полупространства, которое находится в пределах границ окружности радиусом R, которая испытывает однородную нагрузку постоянной интенсивности p 1 = const.
Функция перемещения является необходимым компонентом для 2 площадей: площадь нагружения 0 ≤ r < R (0 ≤p < 1) и для ненагруженной площади R ≤ r < ∞ (1 ≤ p < ∞) интенсивности нагрузки. Для площади 0 ≤ r < R имеем :
и для площади 1 ≤ p < ∞ -
где Se = vz.
После решения интегралов (2) и (3) с применением
Ризык и Градштейном приводят в 1963 (1963, стр. 641) следующий конечный вид формул: для 0 ≤ ρ < 1
и для 1 ≤ p < ∞ -
где K (k, ) и E(k, ) являются эллиптическими интегралами первого и второго типа
и k = ρ, 1/p
Деформация поверхности, выведенная с использованием (6) и (7), четко видна на Рис. 1. Некоторые дискретные значения функции (6) приведены в Таблице 1.
Таблица 1. Дискретные значения безразмерных границ смещения полупространства четко видны на Рис. 1
Рисунок 1. Граница поверхности деформации полупространства,вызванных кольцевой нагрузкой.
2.2 Прямоугольная нагрузка
Решение Буссинеска также можно применить для расчета вертикальных нагрузок, вызванных площадью нагружения прямоугольной формы.
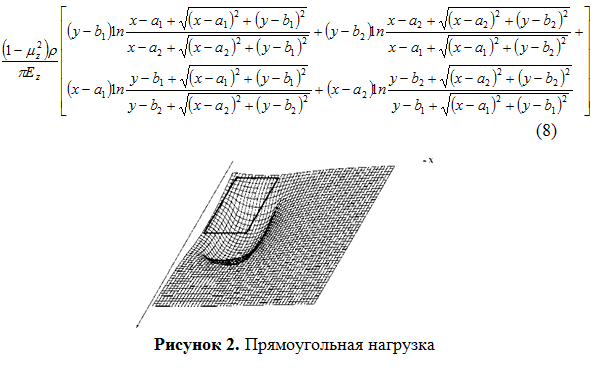
Площадь нагружения находится на поверхности земли, ее длина - а2- а1 и ширина - b2- b1. Однородно распределенная нагрузка на единицу площади равна ρ. Осадку поверхности земли можно рассчитать по формуле :
В этой формуле земная поверхность рассматривается как однородное, изотропное и идеально упругое тело (полупространство) по типу Буссинеска. Эластичные свойства материалов земной поверхности характеризуются модулем продольной упругости Юнга Еz (в GPa) и коэффициентом Пуассона μz (безразмерен). Нагрузка полупространства постоянная, однородная, нормальная. Аналитическое решение основывается на функции нагружения Грина. Прямоугольная нагрузка представлена на Рисунке 2.
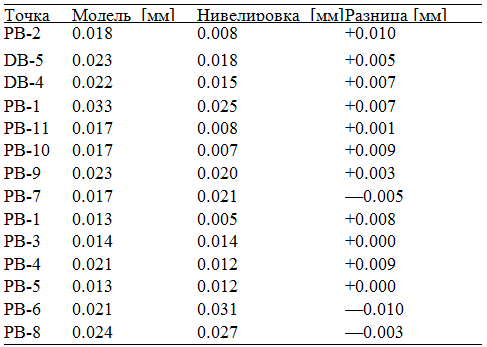
Таблица 2. Различия между расчетными и контролируемыми измерениями при помощи высокоточного нивелирования
2.3 Практический эксперимент
Практический эксперимент был проведен на плотине Габчиково. Плотина Габжиково состоит из двух котлованов. Первый котлован - это водохранилище размером 382 м x 214 м x 33 м и второй котлован – судоходная зона с размерами 429 м x 188 м x 23 м (см. Рис. 3). Выемка грунта из котлована производилась с 1984 по 1986. Вертикальные смещения поверхности земли контролировались посредством высокоточного нивелирования в специальных точках грунтовых реперов (более подробно об этом – смотрите Дженек, 1998). Результаты расчетных деформаций земной поверхности представлены на Рисунке 3. Результаты поднятия земной поверхности, которое контролировалось посредством высокоточного нивелирования в1984 (начало) и 1986 (конец) представлены на Рисунке 4 и в Таблица 2.
Нормальное отклонение различий было подсчитано по формуле :
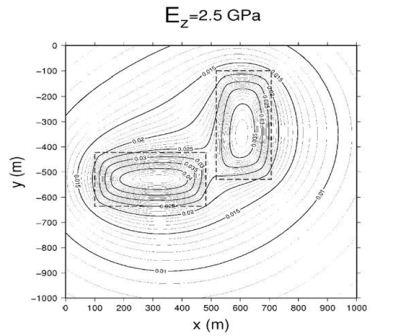
Рисунок 3. Результат поднятия земной поверхности в районе Габчиково.
Измеренные вертикальные смещения в м
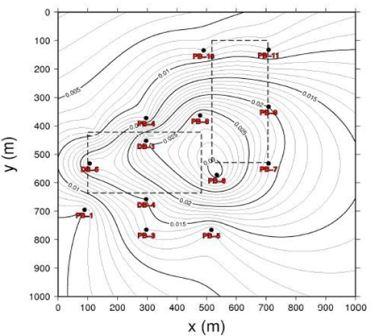
Рисунок 4. Вертикальные смещения, измеренные высокоточным нивелированием (в метрах)
3. Выводы
В статье представлены уравнения для определения вертикальных напряжений в точке в результате приложения кольцевой и прямоугольной нагрузок. Эти уравнения выведены посредством интегрирования уравнения Буссинеска для нагрузки, приложенной в одной точке. Уравнения, представленные в работе, полностью основываются на теории упругости, однако, необходимо учитывать ограничения этой теории в применении к почвенной среде. Это происходит из-за того, что почвенная среда, как правило, не однородна, не идеально упруга и не изотропична. Поэтому, можно предполагать некоторые расхождения с теоретическими подсчетами. На основании результатов, представленных в работе, можно предполагать разницу от ±25% до ±30% между теоретическими оценками и реальными данными, полученными на объекте.
Ссылки
Boussinesq, J. (1885). Applications des potentials a letude de l'equilibre et du mouvement des solides elastiques, Paris, Gauthier - Villars.
Дас, Б. M. (2010). Основы инженерной геологии, 7-ое издание. Cengage Learning. Stamford, CT 06902, США.
Дженек, Дж. (1998). Влияние перемещения масс на изменение уровней в точках контроля сетей, Материалы 1-ой международной конференции по инженерной геодезии INGEO'98 стр. 257-262.
Коллар , П., Мойзес М., Валко, M. (2010). Деформация земной поверхности под влиянием нагрузки от высоких зданий, Slovask Journal of Civil Engineering XVIII(2).
Rektorys, K. (1963). Pfehled uZite matematiky, Statni nakladatelstvl technicke lit- eratury, Praha (in Czech).
RyZik, J., J. Gradstejn (1963). Tablicy integralov, summ rjadov i proizvedenii, Gosud. izdat. fiz-mat. lit., Moskva (in Russian) .