Обоснован алгоритм выбора параметров охраны дегазационных скважин, путем разгрузочного бурения, который позволяет обеспечить устойчивость и герметичность устьев скважин, для создания безопасных условий труда в угольных шахтах.

В большинстве нормативных актов, регламентирующих применение технологий дегазации на угольных шахтах, вопросы охраны скважин освещены недостаточно и нуждаются в доработке [1, 2]. О наличии существенного резерва для повышения эффективности подземной дегазации, при модернизации существующих способов охраны скважин написано немало работ [3, 4], но проблема совершенствования способов их охраны все еще остается недостаточно изученной. В результате зависания породных консолей и сдвижения кровли в выработанном пространстве, может возникнуть угроза устойчивости дегазационной скважины. Рост концентрации напряжений во вмещающем скважину углепородном массиве и интенсификация деформаций стенок обусловлены попаданием ее устья в зону динамического опорного давления, которое начинает проявляться с 40 м впереди лавы [5]. Наиболее близко подошли к разрешению проблемы обеспечения устойчивости подземных дегазационных скважин, при отработке угольных пластов на больших глубинах, специалисты МакНИИ, ДонНТУ и ДонУГИ. МакНИИ одним из первых предложил критерии устойчивости и механизм деформирования дегазационных скважин, а также выявил возможность решения данной проблемы путем оптимизации параметров их пространственной ориентации в породном массиве [6-9]. ДонНТУ, ДонУГИ и ИФГП НАН свои силы сосредоточили на совершенствование менее распространенного способа борьбы с этими явлениями – путем использования разгрузочных скважин [10-12].

Оба этих направления являются перспективными и практически значимыми, и если одно из них необходимо развивать для подземных скважин опережающей дегазации, то другое – для дегазационных скважин, имеющих длительный срок службы. Авторами [13] установлено, что применение способа разгрузки не во всех случаях дает желаемый эффект. Поэтому исследование в области обоснования алгоритма выбора оптимальных параметров охраны методом шпуровой разгрузки, обеспечивающих устойчивость подземных скважин, является актуальной научно-технической задачей для обеспечения безопасных условий труда в угольных шахтах, повышения безопасности ведения горных работ.

Цель работы – разработка алгоритма выбора оптимальных технологических параметров охраны устьев дегазационных скважин путем разгрузочного бурения.

Бурение шпуров необходимо производить концентрично и параллельно оси скважины, в противном случае это может привести к тому, что при интенсификации напряжений, в зоне опорного давления, распределение разгружающего эффекта не будет равномерным по сечению скважины и часть ее может разрушиться. При решении задачи (рис. 1) об определении влияния расстояния между осью скважины и осями шпуров (Rз.к.), радиуса (rш.) и количества шпуров (N) на напряженное состояние контура дегазационной скважины методом конечных элементов использовалась теория Мизиуса-Генки [14]. Перемычка – область массива, ограниченная с одной стороны контуром скважины, а с другой – контурами шпуров. Ширина перемычки – минимальное расстояние между контурами скважины и шпура. Радиусы шпуров вместе с шириной перемычки были представлены относительно радиуса дегазационной скважины (rс.):

Рис. 1. Параметры охраны скважин путем бурения шпуров

Задача решалась в следующей постановке – исследовалась связь между средним значением эквивалентных напряжений на контуре скважины(k' ?) и параметрами бурения шпуров: относительного радиуса шпура (менялся с шагом 0,2), относительной ширины перемычки (L с шагом 0,1) и количества шпуров. Для обеспечения разгрузки значение k' ? должно быть меньшим величины напряжений неразгруженного массива (k'?). По известному решению Динника-Савина [13] k' ? = 2?H. Принимая, что разгрузка должна составлять не менее 10%, то есть k'? ? 1,83 ?H – первое ограничение. В связи исследованиями [13], о влиянии ширины перемычки на величину напряжений было внесено второе ограничение: . Для оптимизации моделирования было проведено технико-экономическое обоснование выбора основных параметров бурения. Главным фактором, принятым во внимание, было отношение общего объема разгрузочного бурения шпуров (Qш., м3, рассчитывалось при длине скважины 120 м) к объему работ по бурению дегазационной скважины (Qс, м3,при длине шпура 5 м). Принималось, что Qш. не должно превышать 40% от Qс.(третье ограничение).Значение объемов бурения, для всех 900 вариантов моделирования, приведены в табл. 1.

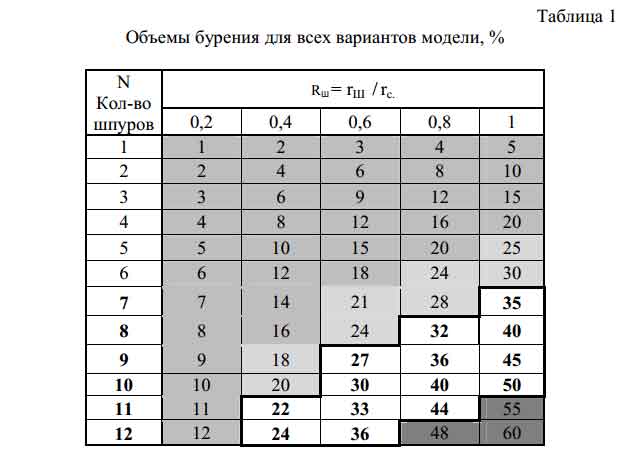
Наиболее темным цветом окрашены ячейки, в которых варианты модели не удовлетворяют ограничению №3, менее темным – ограничение №2 и самым светлым – №1. Жирные значения объемов бурения определяют рациональные варианты моделирования, удовлетворяющие предъявленным выше ограничениям. Расчет коэффициентов концентрации эквивалентных напряжений был осуществлен авторами при использовании метода конечных элементов в работе [11], результаты которой приведены в табл. 2 (для Rш.= 0,4; 0,8 и 1 решены подобные таблицы).

Следующая задача заключалась в создании номограммы (проекции поверхности на плоскость N-L), которая станет основой для разработки алгоритма.

Данные табл. 2 использовались в качестве первичной информации для построения поверхности, отражающей изменение эквивалентных напряжений на контуре скважины от технологических параметров бурения. Было очевидно, что количество точек явно недостаточно для качественного построения проекции этой поверхности на плоскость N-L. В общем виде методика выполнения работы подразумевала выполнение следующих основных этапов: по данным табл. 2 производится построение первичной поверхности, выбирается алгоритм строгой интерполяции для оптимизации поверхности, расчет возможных вариантов аппроксимирующей функции и выбор оптимальной функции по коэффициенту детерминации [14]. В работе использовалась процедура оптимизации в виде алгоритма строгой интерполяции – Watson [15]. Выбор процедуры производится исходя из коэффициента детерминации так, чтобы проекция (на ось XY) оптимизированной поверхности совпадала с проекцией первичной поверхности. Алгоритм строгой интерполяции – специальные программы, создающие линии поверхности, которые точно проходят через исходные точки, при этом сглаживание данных не происходит. В результате проведенных исследований была найдена аналитическая зависимость величины концентрации эквивалентных напряжений на контуре дегазационной скважины от относительной ширины перемычки и количества шпуров при относительном радиусе шпура равном 0,6, которая имеет логарифмический вид (рис. 2) [14].

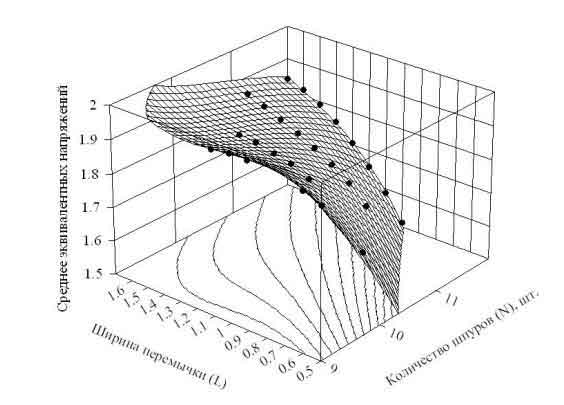
Рис. 2. Функция оптимизированной поверхности

Проекция логарифмической функции на плоскость N–L, представляет собой номограмму (рис. 3), отражающую значение k'? при изменении количества шпуров и относительной ширины перемычки, при использовании которой можно обосновать наиболее рациональные параметры способа шпуровой разгрузки. Кроме того, следует учитывать, что реальные горные породы работают подобно упругим трансверсально-изотропным телам (к которым применимы полученные решения) только вне зоны неупругих деформаций (ЗНД):

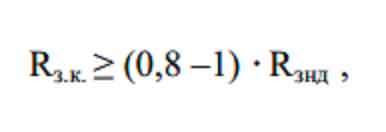
где Rзнд – радиус зоны влияния неупругих деформаций.

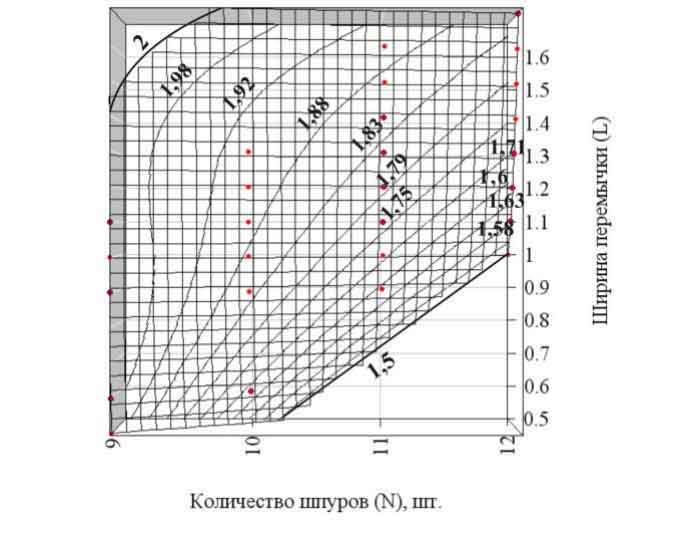
Рис. 3. Значение эквивалентных напряжений

Исходя из того, что естественное напряженное состояние в пластине равняется ??, при наличии отверстия концентрация напряжений составляет 2??, то полученные коэффициенты можно представить в виде процентного соотношения от приращения пригрузки (рис. 4).

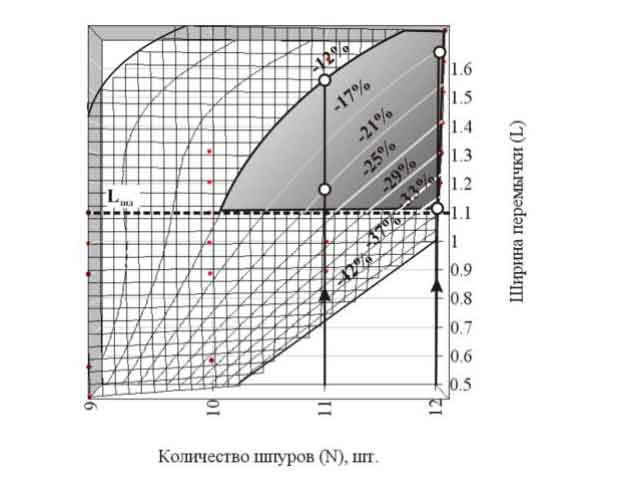
Рис. 4. Поверхность зависимости напряжений

Пример выбора Rз.к. и N для максимального снижения k'?:
1. для глубины 800 м, = 0,027, МН/м3, kc.o. =1, R = 48,5, МН/м2, находим по формуле (3) , которая будет равна 2,3•rв;
2. получим величину эквивалентной перемычки (Lзнд), по формуле, которая образуется между rв и , (причем в нашем случае принимаем по формуле (2), что = 0,9• ): Lзнд = – 1= 0,9 • 2,3 – 1= 1,1• rв;
3. откладываем полученное ограничение Lзнд на ось ординат номограммы и выявляем действительную область значений параметров бурения (см. рис. 4). По номограмме значения процентов снижения напряжений для наличия 11 и 12 шпуров будет находиться в следующих диапазонах: от -12% до -21% при Lш. (1,6-1,2) и от -17% до - 42% при Lш.(1,7–1,1) соответственно;
4. Выбираем наибольшую величину разгрузки (- 42% для 12 шпуров при Rш.= 0,6 и Lш. = 1,1) и определяем коэффициент влияния ЗНД.

ВЫВОДЫ

В результате проведенных исследований были получены следующие результаты: предложен алгоритм выбора оптимальных технологических параметров охраны устьев дегазационных скважин, имеющий длительный срок эксплуатации, путем разгрузочного бурения, который позволяет обеспечить их устойчивость и герметичность; предложена номограмма, отражающую зависимость среднего значения эквивалентных напряжений на контуре скважины от количества шпуров и относительной ширины перемычки при относительном радиусе шпуров 0,6 от радиуса скважины; получили дальнейшее развитие научные основы шпуровой разгрузки, в части – аналитические зависимости концентрации напряжений, на контуре скважины, от относительной ширины перемычки и количества шпуров дополнены современными методиками расчета радиуса ЗНД, при этом формула для определения расстояния между осью скважины и осями шпуров.

CПИСОК ЛИТЕРАТУРЫ

1. Костенко В. К. Изыскание резервов для повышения эффективности подземной дегазации / В. К. Костенко, А. Б. Бокий, В. С. Бригида, Н. Н. Зинченко // 6-я Международная Конференция по проблемегорной промышленности, строительства и энергетике. – Тула: ТулГУ, – 2010. – Т. 1. С. 150–157.
2. Гатаулин Н. Н. Дегазационные системы угольных шахт Украины – фактическое состояние и перспективы развития / Н. Н. Гатаулин, В. К. Костенко, В. С. Бригида, Н. Н. Зинченко // Сб. науч. тр. ДонУГИ. – Донецк: ДонУГИ, 2011. – Вып. 106. – С. 134 – 147.
3. Антипов И. В. Особенности механизма деформации угольного пласта в зоне влияния очистных работ/ И. В. Антипов, Д. В. Щербинин, Р. В. Дегтярь // Физико-технические проблемы горного производства: сб. науч. тр. / ИФГП НАНУ.– Донецк, 2005. – №8. – С. 104 – 111.
4. Назимко В. В. Взрывобезопасность выемочного участка как функция проявления горного давления / В. В. Назимко, П. А. Брюханов // Проблемы горного давления: сб. науч. тр./ ДонНТУ. – Донецк: ДонНТУ, 2009. – №17. – С. 25–62.
5. Назимко В. В. Исследование связи между деформацией дегазационной скважины и ее аэродинамическими параметрами / В. В. Назимко, П. А. Брюханов, А. И. Демченко // Способы и средства создания безопасных и здоровых условий труда в угольных шахтах: сб. науч. тр. / МакНИИ – Макеевка: МакНИИ, 2011. – №2 (26). – С. 25–42.
6. Брюханов П. А. Обоснование критериев устойчивости и эффективности работы дегазационной скважины / П. А. Брюханов, В. В. Назимко, А. А. Резниченко // Донбас-2020: перспективи розвитку очима молодих вчених: матеріали V наук.-практ. конф. м. Донецьк, 25–27 травня 2010. – Донецк: ДонНТУ, 2010. – С. 59–65.
7. Брюханов П. А. Исследование связи между деформацией дегазационных скважины и ее аэродинамическими параметрами /П. А. Брюханов, В. В. Назимко // Способы и средства создания безопасных и здоровых условий труда в угольных шахтах: сб. науч.тр. / МакНИИ – Макеевка: МакНИИ, 2012. – №2 (28). – С. 198 – 211.
8. А.с. № 817253 СССР, МКИ3 Е21 С 37/00; Е 21Д 9/00. Способ проходки выработки / В. К. Костенко, М. П. Зборщик, А. Ф. Морозов (СССР). – №2761683/22-03; заявл. 03.05.71, опубл. 30.03.81, Бюл. №12.
9. Стариков Г. П. Физико-механическое обоснование параметров разгрузочных скважин / Г. П. Стариков, Д. В. Мельников, Н. И. Волошина, В. Н. Чистоклетов // Физико-технические проблемыгорного производства: сб. науч. тр. / ИФГП НАНУ.– Донецк, 2005. – №8. – С. 129 – 133.
10. Мельников Д. В. Основы метода расчета параметров разгрузочных скважин / Д. В. Мельников // Физико-технические проблемы горного производства: сб. науч. тр. / ИФГП НАНУ.– Донецк, 2011. – №14. – С. 93 – 98.
11. Костенко В. К. Закономерности формирования области разгрузки, обеспечивающей сохранность устьев дегазационных скважин / В. К. Костенко, В. С. Бригида, Н. Н. Зинченко // Проблемы горного давления: сб. науч. тр. /ДонНТУ. – Донецк: ДонНТУ, 2012. – №17. – С. 205–212.
12. Филоренко-Бородич М. М. Механические теории прочности / М.М. Филоренко-Бородич. – М., 1951. – С. 18–23. 13. Савин Г. Н. Распределение напряжений около отверстий. – К.: Наукова думка, 1968. – 854 с.
13. Костенко В. К. Обоснование параметров способа шпуровой разгрузки устьев дегазационных скважин / В. К. Костенко, В. С. Бригида, Н. Н. Зинченко // Физико-технические проблемы горного производства: сб. науч. тр. / ИФГП НАНУ.– Донецк, 2012. – №15. – С. 93 – 98.
14. Watson D. nngridr: An Implementation of Natural Neighbor Interpolation, Claremont, Australia, – 1994. – 170 с.
15. Предупреждение и тушение подземных эндогенных пожаров в труднодоступных местах: монография / В. К. Костенко, Ю. Ф. Булгаков, С. В. Подкопаев [и др.] – Донецк: Ноулидж, 2010. – С. 100.