Назад в библиотеку

---

Анизотропная пластичность (ANISO)

4.1.9. Анизотропная пластичность (ANISO)

Модель анизотропной пластичности использует критерий текучести Хилла [50], который учитывает различия пределов текучести в ортогональных направлениях и модифицирован Shin и Lee [51] на случай различных пределов текучести при растяжении и сжатии. Критерий текучести может меняться с ростом пластических деформаций благодаря использованию ассоциированного закона течения и изотропного упрочнения в форме, представленной Valliapanetal [52]. Таким образом, поверхность текучести представляет собой круговой цилиндр, который изначально сдвинут в пространстве напряжений и увеличивается в размерах с ростом пластических деформаций (Рис. 4.1-2в).

Эквивалентные напряжения для этой модели определяются следующим выражением:

s_e = 1/3 {s}^T [M] {s} – 1/3 {s}^T{L}, (4.1-33)

где [M] - матрица, описывающая вариации напряжения текучести в зависимости от ориентации, а вектором {L} учитывается различие между пределами текучести при растяжении и сжатии. Вектор {L} может быть связан с вектором смещения поверхности текучести {a} с помощью уравнения (4.1-24) (Shin и Lee [51]), следовательно, функцию эквивалентных напряжений можно интерпретировать как имеющую начальное смещение, или сдвиг. Текучесть материала возникает в случае, когда эквивалентное напряжение s_e становится равным параметру материала К. Критерий текучести (уравнение (4.1-4)) имеет вид:

3 F = {s}^T [M] {s} – {s}^T{L} - K = 0. (4.1-34)

Предполагается, что материал имеет три ортогональные плоскости симметрии. Пластическое поведение может характеризоваться соотношениями "напряжения-деформации”для трех направлений системы координат элемента и соответствующими соотношениями для напряжений и деформаций сдвига. Следовательно, матрица [M] имеет вид:

	М11	М12	М13	0	0	0
	М12	М22	М23	0	0	0
М =	М13	М23	М33	0	0	0	(4.1-35)
	0	0	0	М44	0	0
	0	0	0	0	М55	0
	0	0	0	0	0	М66

Если найти критерий текучести (уравнение (4.1-34)) для всех возможных случаев одноосных напряжений, можно найти выражения для отдельных компонент матрицы [M], а именно:

M_jj= K/(s_+js_-J), j = 1…6, (4.1-36)

где s_+J, s_-J представляют собой пределы текучести на растяжение и сжатие в направлении j (j=x, y, z, xy, xz, yz). В данном случае, напряжение текучести при сжатии считается положительной величиной. При текучести сдвига s_+J= s_-J. Принимая M₁₁=1, находим К

К = s_+J * s_-J. (4.1-37)

Дифференциальный вектор прочности {L} имеет вид:

{L} = ëL₁L₂ L₃ 0 0 0 û^T, (4.1-38)

компоненты которого определяются одноосными условиями нагружения следующим образом:

L_j= M_jj (s_+j- s_-J), j = 1…3. (4.1-39)

Предположив несжимаемость материала при пластических деформациях (то есть, отсутствие изменения объема материала по мере роста пластических деформаций), получим следующие соотношения:

M₁₁+ M₁₂ + M₁₃ = 0,

M₂₁+ M₂₂ + M₂₃ = 0, (4.1-40)

M₃₁+ M₃₂ + M₃₃ = 0

и

L₁ + L₂ + L₃ = 0. (4.1-41)

Итак, внедиагональные элементы матрицы [M] выражаются следующим образом::

M₁₂= -1/2 (M₁₁ + M₂₂ - M₃₃),

M₁₃= -1/2 (M₁₁ - M₂₂ + M₃₃), (4.1-42)

M₂₃ = -1/2 (-M₁₁ + M₂₂+ M₃₃).

Заметим, что из уравнения (4.1-41) (с учетом уравнений (4.1-36) и (4.1-39)) следует соотношение, обусловленное пластической несжимаемостью:

s+x - s-x	+	s+y - s-y	+	s+x - s-x	= 0 (4.1-43)
s+x s-x		s+y s-y		s+x s-x

Таким образом, предел текучести не является полностью независимой величиной.

Пределы текучести должны задавать замкнутую поверхность текучести с эллиптическим поперечным сечении. Эллиптическая поверхность текучести определяется в том случае, если выполняется следующее условие:

M₁₁²+ M₂₂² + M₃₃² – 2(M₁₁M₂₂+ M₂₂M₃₃ + M₁₁M₃₃) < 0. (4.1-44)

В противном случае будет выдано следующее сообщение: "THE DATA TABLE DOES NOT REPRESENT A CLOSED YIELD SURFACE. THE YIELD STRESSES OR SLOPES MUST BE MADE MORE EQUАL” ("ТАБЛИЧНЫЕ ДАННЫЕ НЕ ПРЕДСТАВЛЯЮТ ЗАКРЫТУЮ ПОВЕРХНОСТЬ ТЕКУЧЕСТИ. ПРЕДЕЛЫ ТЕКУЧЕСТИ ИЛИ ТАНГЕНСЫ УГЛОВ НАКЛОНА ДОЛЖНЫ БЫТЬ БОЛЕЕ БЛИЗКИМИ”). Это в дальнейшем ограничит независимость одноосного предела текучести. Так как предел текучести изменяется с пластической деформацией (как следствие пластической работы), это условие должно удовлетворять для всей истории нагружения. Программа проверяет это условие при возрастании эквивалентных пластических деформаций на 20%.

Для изотропного материала:

M₁₁= M₂₂ = M₃₃ = 1

M₁₂= M₁₃ = M₂₃ = -1/2

M₄₄= M₅₅ = M₆₆ = 3

и

L₁= L₂ = L₃ = 0.

Критерий текучести (уравнение (4.1-34)) приводится к критерию Мизеса (уравнение (4.1-26) при {a}=0).

В качестве закона упрочнения используется изотропное упрочнение, так что при увеличении общей пластической работы предел текучести материала также возрастает. Общая пластическая работа определяется уравнением (4.1-20), в котором приращение работы выражается формулой:

Dc = {s*}^T {DÎ^pl}, (4.1-45)

где {s*} - среднее напряжение в пределах приращения.

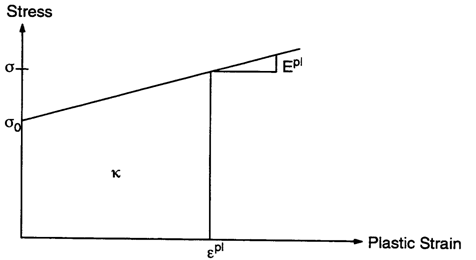
Рис. 4.1-4. Пластическая работа при одноосном нагружении

При одноосном нагружении общая пластическая работа определяется просто:

c= 1/2 Î^pl(s₀+s), (4.1-46)

(обозначения см. на Рис. 4.1-4).

Для модели билинейного поведения материала имеет место соотношение:

s = s₀+ E^plÎ^pl, (4.1-47)

где тангенс угла наклона пластического участка E^plопределяется значениями упругого и касательного модуля:

E^pl = EE_T/(E – E_T). (4.1-48)

Из уравнения (4.1-47) с учетом (4.1-46) следует формула для модифицированного значения напряжения текучести:

s= s {2 E^pl c + s₀²}^1/2. (4.1-49)

Распространяя этот результат на анизотропный случай, будем иметь:

s_j = {2 E_j^plc+ s_0j²}^1/2. (4.1-50)

Индекс j относится к каждой из заданных кривых "s-e”. Уравнение (4.1-50) определяет модифицированные значения напряжения текучести путем приравнивания пластической работы в материале эквивалентной работе для каждого направления.

Затем могут быть обновлены параметры [M] и {L}, исходя из данных для них определений (уравнения (4.1-36) и (4.1-39)) и значения напряжений текучести. Для изотропных материалов этот закон упрочнения сводится к случаю изотропного упрочнения.

Эквивалентные пластические деформации Î*^pl (выходная величина EPEQ) вычисляются подстановкой уравнения (4.1-47) в уравнение (4.1-46), в качестве справочной оси принимается положительное направление оси х (соответствует растяжению):

Î*^pl= [-s_+x+ (s²_+x + 2 cE_+x^pl)^1/2]/E_+x^pl, (4.1-51)

при этом в качестве напряжения текучести s_+xпри растяжении в направлении оси х принимается начальное (не обновленное) значение напряжения текучести. Параметр эквивалентного напряжения s_е^pl(выходная величина SEPL) определяется формулой:

s_е^pl= s_+х^pl + E*_+x^pl Î, (4.1-52)

где s_+х , как и прежде, начальные напряжения текучести.