Назад в библиотеку

---

2.1. Основы прочностного анализа

2.1.1. Соотношения "напряжения–деформации”

Описание: В этом разделе рассмотрены физические соотношения для материалов с линейными свойствами.

{s} = [D] {e^el}, (2.1-1)

где {s} = ës_xs_ys_zs_xys_yzs_xzû^Т - вектор напряжений (как выходная величина помечается меткой S);

[D] – матрица упругости (описывается уравнениями (2.1-18) … (2.1-23), обратная матрица записывается в виде (2.1-4) и (2.1-5); для некоторых анизотропных элементов эта матрица вводится командами TBDATAс опцией TB,ANEL.);

{e^el} = {e} – {e^th} - выходной массив EPEL;

{e} =ëe_x e_ye_ze_xye_xze_yzû^Т - вектор полной (суммарной) деформации;

{e^th} – вектор температурной деформации (определяется соотношением (2.1-3), выходной массив EPTH).

Выходная величина EPEL представляет собой вектор деформаций, которые вызывают напряжения, т.е. {e} – {e^th}.

Замечание: в постпроцессоре POST1 подобная же величина EPTO, именуемая "компонентом суммарной деформацмм (component total strain)", может использоваться для маркировки оси деформаций при построении нелинейных кривых "s-e”. Составляющие приведенного выше вектора полной деформации {e} можно трактовать как деформации, которые измеряются соответствующим датчиком. Эти два "полных" набора деформаций отличаются наличием или отсутствием вектора температурной деформации.

Компоненты вектора напряжений показаны на Рис. 2.1-1. Для используемых в программе ANSYS напряжений и деформаций принято следующее правило знаков: величины, относящиеся к растяжению являются положительными, к сжатию - отрицательными. Компоненты сдвига считаются положительными, если их направления совпадают с направлениями соответствующих координатных осей. Деформации сдвига представляют собой инженерные деформации, а не компоненты тензора.

 

 

Рис. 2.1-1. Компоненты вектора напряжений

Уравнение (2.1-1) может быть обращено следующим образом:

{e} = {e^th} + [D]^-1{s}. (2.1-2)

Для трехмерного случая вектор температурных деформаций определяется в виде соотношения

{e^th} = DT ëa_x a_y a_z 0 0 0 û^T, (2.1-3)

где a_x – коэффициент температурного расширения в направлении оси х (вводится в виде параметра ALPX командойМР),

DT = T – T_REF,

T – текущая температура в интересующей точке,

T_REF – температура, при которой деформации отсутствуют (вводится командой TREF).

Матрица [D]^-1, нормализованная по столбцам, имеет вид:

 

 

Если используется нормализация по сторокам, то эта матрица записывается следующим образом:

 

Для записи элементов этих матриц используются обозначения:

E_x – модуль Юнга в направлении оси х (вводится как параметр ЕХ командой МР),

n_xy – минимальный коэффициент Пуассона (вводится как параметр NUXY

командой МР),

n*_xy– максимальный коэффициент Пуассона (вводится как параметр PRXY

командой МР),

G_xy – модуль сдвига в плоскости х-у (вводится как параметр GXY командой МР).

Матрица [D]^-1должна быть положительно определенной (см. раздел 13.5). Кроме того, эта матрица должна быть симметричной, поэтому для ортотропных материалов предполагается существование соотношений:

n_yx / E_x= n_xy / E_y

n_zx / E_x= n_xz / E_z

n_zy / E_y= n_yz / E_z

или

n*_yx / E_y = n*_xy/ E_x

n*_zx / E_z = n*_xz/ E_x

n*_zy / E_z = n*_yz/ E_y

Согласно приведенным выше соотношениям, величины n_xy, n_zy, n_zx, n*_yx, n*_zy иn*_zx являются зависимыми и поэтому не задаются при вводе исходных данных.

Использование конкретных значений для коэффициентов Пуассона при анализе ортотропных материалов иногда приводит к затруднениям, поэтому к этому следует подходить с осторожностью. Обычно для ортотропных материалов бывают известны значения n*_ху, или главного коэффициента Пуассона (PRXY). Величина n*_хусчитается главным коэффициентом Пуассона, поскольку это значение больше, чем n_ху, если исходить из того, что E_х превосходит E_у.

Для упрощения в остальной части этого раздела будут использоваться только параметры n_xy, n_zy, n_zx. Для изотропных материалов выполняются условия E_х = E_y = E_z и n_xy = n_zy = n_zx, поэтому ввод исходных данных не вызывает затруднений. Для ортотропных материалов требуется проверять соответствие приведенных в справочной литературе данных требуемому формату ввода.

Если переписать равенство (2.1-2) в развернутом виде, используя выражения (2.1-3), (2.1-4), а также (2.1-6) ... (2.1-8), то получим шесть уравнений:

e_x = a_x DT + s_x /E_x- n_xy s_y / E_y- n_xz s_z / E_z (2.1-12)

e_y = a_y DT + s_y /E_y- n_xy s_x / E_y- n_yz s_z / E_z (2.1-13)

e_z = a_z DT + s_z /E_z- n_xz s_x / E_z- n_yz s_y / E_z (2.1-14)

e_xy = s_xy /G_xy (2.1-15)

e_yz = s_yz /G_yz (2.1-16)

e_xz = s_xz /G_xz, (2.1-17)

где e_x - деформация в направлении оси х,

e_xy - деформация сдвига в плоскости х - у,

s_x - напряжения в направлении оси х,

s_xy - напряжения сдвига в плоскости х - у;

компоненты с другими индексами получаются циклическим сдвигом (x - y- z).

С другой стороны, уравнение (2.1-1) можно переписать в развернутом виде, используя обратную матрицу (2.1-4), что вместе с уравнениями (2.1-3), (2.1-6) ... (2.1-8) дает шесть соотношений для напряжений:

sx = Ex/h [1 - (nyz)2 Ey/Ez] (ex - ax DT) + Ex/h [nxy + nxznyz Ey/Ez] (ey - ay DT) + Ex/h [nxz + nyznxy] (ez - az DT)	(2.1-18)
sy = Ex/h [nxy + nxznyz Ey/Ez] (ex - ax DT) + Ey/h [1 - (nxz)2 Ex/Ez] (ey - ay DT) + Ey/h [nyz + nxznxy Ex/Ey] (ez - az DT)	(2.1-19)
sz = Ex/h [nxz + nyznxy] (ex - ax DT) + Ey/h [nyz + nxznxy Ex/Ey] (ey - ay DT) + Ez/h [1 - (nxy)2 Ex/Ey] (ez - az DT)	(2.1-20)
sxy = Gxy Îxy	(2.1-21)
syz = Gyz Îyz	(2.1-22)
sxz = Gxz Îxz,	(2.1-23)

в которых обозначено: h = 1 - (n_xy)²E_x/E_y - (n_yz)² E_y/E_z - (n_xz)²E_x/E_z - 2 n_xy n_yz n_xz E_x/E_z.

Если модули сдвига G_xy, G_yz, G_xz не задаются при вводе, то их значения вычисляются следующим образом:

G_xy= (E_x E_y) / (E_x + E_y + 2 n_xy E_x) (2.1-24)

G_yz= G_xy (2.1-25)

G_xz = G_xy (2.1-26)

Такие значения используются по умолчанию и предназначены только для изотропных материалов, поэтому при задании свойств ортотропных материалов пользователь должен убедиться, что справочное пособие по свойствам материала содержит нужное значение модуля сдвига.

Матрица [D] должна быть положительно определенной. Программа проверяет значение каждого задаваемого параметра материала, чтобы гарантировать положительную определенность этой матрицы. В случае зависящих от температуры свойств материала такая проверка выполняется при одинаковой температуре (командаBFUNIF) на первом шаге нагружения. Если материал изотропный или n_xy, n_y и n_xz равны нулю, то матрица [D] будет всегда положительно определенной. Примером материала, нарушающим положительную определенность матрицы [D], служит материал, для которого выполняется условие E_у£ E_х(n_xy)².

 

2.1.2. Задание ортотропных свойств для осесимметричной модели

Преобразование параметров материала для расчетной модели, заданной в цилиндрической системе координат R-q-Z, в декартову систему x-у-z, в которой программой ANSYS предусмотрен ввод исходных данных, требует осторожности. Преобразование модуля Юнга выполняется однозначно, тогда как правильный способ преобразования коэффициента Пуассона не столь очевиден. Рассмотрим сначала, как преобразуется модуль Юнга из глобальной цилиндрической системы в глобальную декартову систему при использовании осесимметричных элементов для расчетной модели в виде диска:

в действительности как осесимметричный элемент

 

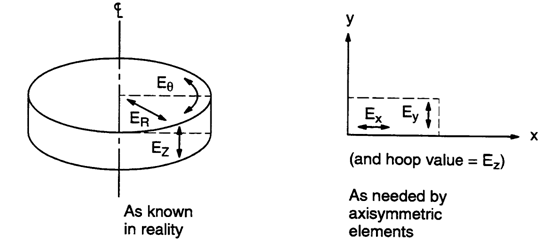
Рис. 2.1-2. Системы координат для материалов

Нетрудно видеть, что преобразование состоит в замене: E_R ® E_x, E_q ® E_z и Ez ® E_у. В программе ANSYS ввод коэффициентов Пуассона, снабженных метками NUXY, NUYZ, NUXZ, осуществляется в глобальной декартовой системе координат соответственно для направлений x - y - z с помощью команды МР, после чего создается следующая согласованная матрица для нормальных напряжений, нормализованная по столбцам:

Предположив, что значения коэффициентов Пуассона в цилиндрической системе координат R - q - Z можно представить подобным же образом, получим, что согласованная матрица для этого случая имеет вид (2.1-27). Если потребовать соответствия осей R - q - Z осям x - y - z (то есть, x ® R, y ® Z, z ® q), то получим матрицу:

В результате поэлементного сопоставления матриц (2.1-27) и (2.1-28), можно получить следующие соотношения:

E_x = E_R (2.1-29)

E_y = E_z (2.1-30)

E_z = E_q (2.1-31)

n_xy = n_Rz = E_q/E_z n_zq (2.1-32)

n_yz = n_zq (2.1-33)

n_xz = n_qR (2.1-34)

Левая часть этих соотношений представляет собой входные данные (параметры NUXY, NUYZ, NUXZ), правая - преобразование этих данных с нормализацией по столбцам.

Если для входных данных использовать преобразование с нормализацией по строкам, то в этом случае согласованная матрица примет вид:

Сравнение матриц(2.1-27) и (2.1-35) позволяет получить такие соотношения:

E_x = E_R (2.1-36)

E_y = E_z (2.1-37)

E_z = E_q (2.1-38)

n_xy = E_z/E_Rn*_Rz (2.1-39)

n_yz = n*_zq = n*_qz (2.1-40)

n_xz = E_q/E_R n*_qR (2.1-41)

Здесь, как и прежде, левая часть этих соотношений представляет собой входные данные (параметры NUXY, NUYZ, NUXZ), но теперь правая часть - это преобразование данных с нормализацией по строкам.

В программе ANSYS ввод данных для уравнений (2.1-29) ... (2.1-34) и (2.1-36) ... (2.1-41) можно также осуществить, используя метки PRXY, PRYZ и PRXZ с соответствующими дополнительными преобразованиями.

 

2.1.3. Зависимость коэффициента температурного расширения

от температуры

В уравнении (2.1-3) компонента температурной деформации имеет следующий вид:

Î^th = a(T) (T - T_ref). (2.1-42)

При этом предполагается, что коэффициент a не является функцией температуры. Если предположить, чтоa зависит от температуры, то уравнение (2.1-42) запишется таким образом:

Î^th =ò_Tref a_inst (T)dT, (2.1-43)

где a_inst (T) - так называемый мгновенный коэффициент температурного расширения.

В программе, однако, используется среднее, или средневзвешенное, значение коэффициента a, которое дает возможность получить значение температурной деформации в виде уравнения (2.1-42):

Î^th = a*(T) (T - T_ref), (2.1-44)

где a*(T) = ò_Tref (a_inst/(T - T_ref)) dT - cреднее значение коэффициента температурного расширения, введенного в виде ALPX, ALPY или ALPZ командой МР.

Обычно исходные данные приводятся в справочной литературе как некоторые средние значения, и эти данные корректно используются в программе до тех пор, пока величина T_refявляется не только температурой, при которой можно использовать справочные данные, но и температурой, при которой отсутствуют температурные деформации. Если это условие не выполняется, необходимо исправить значение коэффициента температурного расширения. Рассмотрим следующие выражения:

Î₀^th = a⁰*(T) (T - T₀) = ò_T0 a_inst dT, (2.1-45)

Î_r^th = a^r*(T) (T - T_ref) = ò_Tref a_inst dT. (2.1-46)

Уравнения (2.1-45) и (2.1-46) определяют температурную деформацию при температуре T для разных начальных точек: T₀и T_ref. Предположим, что T₀ - это температура, в окрестности которой определялось значение коэффициента a (температура определения), а T_ref- температура, при которой отсутствуют температурные деформации (справочная температура). Таким образом, a⁰*(T) - это взятая из справочной литературы величина, а коэффициент a^r*(T) – это величина, которую требуется вводить как исходную.

Правую часть уравнения (2.1-45) можно представить следующим образом:

ò_T0 a_inst dT = ò_T0 a_inst dT + ò_Tref a_inst dT , (2.1-47)

кроме того,

ò_T0 a_inst dT = a⁰*(T_ref) (T_ref- T₀) (2.1-48)

или

ò_T0 a_inst dT = a^r*(T₀) (T_ref- T₀) . (2.1-49)

Из соотношений (2.1-45) … (2.1-48) следует основное равенство:

a^r*(T) = a⁰*(T) + (T_ref - T₀) / (T- T _ref) (a⁰*(T) - a⁰*(T_ref)). (2.1-50)

Итак, уравнение (2.1-50) следует использовать, когда требуется учесть различие температуры, при которой определялся коэффициент a, и температуры, при которой отсутствуют температурные деформации. Это делается автоматически при использовании команды MPAMOD.

Заметим, что если T_ref = T₀, уравнение (2.1-50) принимает простейший вид.

Следует обратить внимание, что при T = T_refуравнение (2.1-50) не определено. Поскольку используемые значения T являются температурами, задаваемыми командой MPTEMP, то при ее использовании рекомендуется избегать задания T, равного T_ref с погрешностью в один градус. Если значение T = T_refи

·величина Т равна любому из крайних значений введенного интервала температур, то коэффициент a принимает значение, соответствующее ближайшей соседней точке;

·величина Т не равна ни одному из крайних значений введенного интервала температур, то коэффициент a равен средней величине двух новых соседних значений.