Аннотация
Bagordo О.G., Cazzulani G., Resta F., Ripamonti F. - Модальный оценщик волнения для подавления вибрации в нелинейных гибких структурах Эта работа представляет стратегию управления для подавления вибрации из-за неизвестных сил волнения в больших, нелинейных гибких структурах. Предложенные меры контроля, основанные на модальном подходе, состоят из двух вкладов. Первым является известный Независимый Модально-пространственное управление, которое увеличивает системное демпфирование и улучшает его поведение близкое к частотам резонанса. Вторым является оценщик волнения, который вычисляет модальные компоненты внешних сил, действующих на систему, и компенсирует за них использующий силы приводного механизма. Система модальных координат, требуемая обеими логиками, оценена через модального наблюдателя состояния. Предложенная логика контроля проверена на гибком манипуляторе. Статья сообщает о численных и экспериментальных данных для линейной и для нелинейной конфигураций манипулятора.
1. Введение
Гибкие структуры обычно характеризуются низкими отношениями демпфирования и, как следствие, высокой чувствительностью к внешним воздействиям, вызывающим высокие уровни вибрации и высокое механическое усилие. Эти колебания уменьшают срок работы системы и, в случае сотрудничества человеческой машины, ставят под угрозу безопасность оператора. За эти годы много активных методов контроля были развиты, чтобы рассеять энергию системы. Один из самых привлекательных для гибких структур - известный Независимое модальное управление состояния (НМУС) [1-4]. Этот метод основан на модальном подходе, уплотняя непрерывную структуру в конечное множество способов вибрации, связанных с глобальным движением системы. Контроль за НМУС действует непосредственно на динамику системы, изменяя ее собственные значения и улучшая системную стабильность. В следующем некоторые улучшения НМУС были предложены, такие как Модифицированное независимое модальное управление состояния (МНМУС) [5, 6] и Рациональное модальное управление (РМУ) [7] первый уменьшает так называемую проблему ''избытка'' [8, 9], в то время как второе уменьшает энергичное усилие контроля. Помимо многих других стратегий управления, в общем названных ‘‘резонансный контроль’’, были развиты, чтобы улучшить системные действия близко к ее естественным частотам. Самый известный резонансный контроль - вероятно, позиционирование с использованием положительной обратной связи [10-12].
Если возмущения, действующие на систему, подвергнуты большим и быстрым изменениям, описанные стратегии управления с обратной связью очень часто неспособны содержать системную вибрацию в желаемых пределах. В частности и модальные и резонансные методы контроля не улучшают системную работу, далекую от ее естественных частот. Ситуация может стать очень важной, если, например, система подвергнута силам высокого уровня в квазистатической зоне (ниже первой естественной частоты).
Если возмущения непосредственно измеримо, возможно минимизировать свой эффект, вводя пропорциональное действие. Эту операцию также называют ‘‘компенсацией возмущения’’ и, в целом, это может быть использовано дополнительно к действию обратной связи, это предугадывается, потому что это действует на вход системы, и ее внедрение требует модели процесса. В литературе большое количество компенсаторов [13], проанализированы. К сожалению, в общем применении не всегда возможно измерить входы системы. В этих ситуациях возмущения должны быть оценены и компенсированы с помощью системы контроля усилий [14, 15].
В этой статье представлен алгоритм, который позволяет отклонять возмущения в системе, даже если они не измеримы. Начинаясь со знания системной модели и рассматривая модальный подход, от ряда измерений, логика контроля оценивает внешний вклад возмущения и отменяет его, вводя обратное действие через приводной механизм. Ниже этого компенсатора будет назван оценщик возмущения (ОВ). Поэтому получающаяся логика контроля состоит из двух различных вкладов, действующих одновременно на систему: действие обратной связи НМУС, чтобы увеличить системное демпфирование и ОВ, чтобы дать компенсацию за внешние силы, действующие на систему.
Ради полноты первая секция суммирует теорию Независимого Модально управления состоянием, в то время как во втором методика оценки возмущения представлена. В следующем параграфе проблема модальной координационной оценки полностью решена, рассматривая наблюдатель модального состояния. Наконец, числовые и экспериментальные тесты были выполнены, чтобы оценить действия контроля и для линейного и нелинейного случая.
2. Логика управления
2.1 Независимое модальное управление состоянием.
Для того чтобы рассмотреть НМУС, рассмотрим уравнение движения универсальной механической системы

где fc - вектор сил контроля, действующих на систему, и [∧F]T-отсылает их к приводному механизму. Фактически роль матрицы должна соединить силы приводного механизма с соответствующими центральными компонентами структуры. [M], [R] и [K], соответственно, инерционное, затухающие и жесткие системы матрицы, в то время как zпредставляет вектор системных координат. Возможно оценить собственные значения и собственные векторы Фj из не дифференцированного однородного уравнения

Определение m число продуманных способов, и

матрица собственного вектора, преобразование в основных координатах может быть получено как

Использую ур. (4), ур. (1) получаем
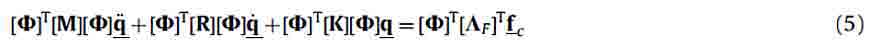
Под предположением демпфирования Рэлея

в котором параметры α and β могут быть экспериментально оценены, ур. (5) становится рядом m разделенные уравнения

Предположение демпфирования Рэлея позволяет определять систему затухания как функцию только двух параметров. Ценность этих параметров была идентифицирована, чтобы лучше всего соответствовать отношениям демпфирования продуманных способов.
Действие контроля непосредственно в зависимости от модальных координат может быть определено как

где [GD] и [GP]- матрицы усиления. Представление ур. (8) в ур. (7), это становится

Если [GD] и [GP] - диагональные матрицы, возможно изменить системные собственные значения друг независимо от друга. Кроме того, системные собственные векторы не изменяются, потому что уравнения движения в модальных координатах для системы, которой управляют, остаются разделенными, и динамика универсального способа описана

Два усилителя gdi и gpi - позволяют полюс способ вибрации быть ассигнованным. Фактически, выбирая положение полюсов системы, которой управляют,  как
как

и запоминание отношений между массой, демпфирование и жесткостью и системными собственными значениями

усиление может быть получено через отношения

Два усиления непосредственно изменяет соответственно демпфирование и жесткость каждого системного способа. В любом случае изменение жесткости (и как следствие естественное изменение частоты) требуют очень высоких сил контроля в общих механических заявлениях. Эти силы увеличивают материальное напряжение и могут привести к проблемам здоровья структуры. Кроме того, в случае ошибок по естественной оценке частот, высоко управляйте силами, может привести к непредсказуемому системному поведению и, в некоторых случаях, к нестабильности системы, которой управляют. По этим причинам очень часто выбор gpi=0 применен, чтобы изменить только системное демпфирование и оставить его поведение неизменным в частотах далекий от естественных.
2.2 Оценщик волнения
Решение рассмотреть только производный вклад модальных компонентов делает НМУС довольно слабый для волнения, действующих в регионе нерезонанса. Кроме того, модальный вклад контроля не очень эффективный при отмене системного ответа внешним силам волнения, когда их гармоническое содержание находится в квазистатическом или сейсмическом регионе. Чтобы преодолеть этот предел, компенсатор волнения может быть принят. Рассмотрение волнения вызывает di. От модального уравнения движения (7), можно рассмотреть универсальное это уравнение

где управления силой ƒci - сумма вклада НМУС (определенный в Разделе 2.1) и вклада ОВ 

Вклад ОУ получен, умножая волнение, оцененное в предыдущем шаге  интеграции со стороны усиления Gi который будет определен в следующем. Чтобы вычислить вклад ОУ, вспомогательная система, равная реальной, может быть введена. Вспомогательная система вызвана всеми известными силами, относился к реальной системе (в этом случае только контроль один)
интеграции со стороны усиления Gi который будет определен в следующем. Чтобы вычислить вклад ОУ, вспомогательная система, равная реальной, может быть введена. Вспомогательная система вызвана всеми известными силами, относился к реальной системе (в этом случае только контроль один)

где pi модальная координата, представляющая компонент системных колебаний только благодаря известным силам. Если для каждого шага интеграции начальное условие реальной системы рассматривают, и числовая модель системы, оказывается, равна реальной системе, ур. (16) может быть вычтен из ур. (14)

так, чтобы μi=qi-pi представлял вклад в систем у вибраций только благодаря неизвестным возмущениям. Теперь универсальный модальный компонент di сил возмущения может быть получен, решая инверсию, динамичную из ур. (17), так как μi известны. Эти силы, восстановленные и с противоположным знаком, могут быть применены к системе, чтобы дать компенсацию за эффекты возмущения ур. (15). С теоретической точки зрения полная обратная связь восстановленной силы в состоянии полностью отменить вибрацию из-за возмущения. Так или иначе, из-за различий между моделью и реальной системой (ошибки в идентификации системных параметров, заброшенных способов, и т.д.) Предполагаемое возмущение не будет равно реальному. Как следствие полная обратная связь могла ухудшить действия контроля. Поэтому усиление Gi введена для каждого модального компонента возмущения. Эта выгода - число между 0 и 1 и представляют ''надежность'' предполагаемого возмущения Gi=1 означает полную обратную связь предполагаемого возмущения, в то время как 1 означает полную обратную связь предполагаемого возмущения, в то время как Gi=0 означает, что никакая обратная связь не обеспечена оценщиком возмущения.
2.3. Модальная оценка координат
Соображения в предыдущем параграфе выдвигают на первый план важность модального процесса оценки компонентов. Фактически это затрагивает обоих предложенные логики контроля. Оценка может привести к значительным проблемам на более поздних стадиях. Краткий обзор модальной оценки компонентов предложен. От ур. (1), уравнение состояния системы, которой управляют, может быть определено как

где x представляет вектор пространства состояний, y представляет вектор измерений, [C] - отношения между измерениями и системными координатами, измерения и системные координаты, [D] тождественно пустой с тех пор в этом применении, только скоростные измерения рассматривают. Начиная с значений y измерений, возможно получить систему модальные компоненты, используя состояние наблюдателя. Наблюдатель состояния - модель, воспроизводящая внутреннюю динамику механической системы, в которой предполагаемая продукция y постоянно по сравнению с измерениями y собрана из системы. В этом применении, основанном на модальных компонентах, необходимо переключиться на модальные координаты посредством ур. (4). В частности рассматривая представление пространства состояний, возможно определить

где qm, представляя модальный вектор пространства состояний, содержит модальные скорости и смещения. Следовательно

Предполагаемые модальные координаты  могут быть получены через модальный наблюдатель состояния, определенного
могут быть получены через модальный наблюдатель состояния, определенного
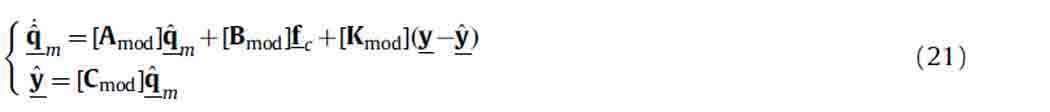
матрица усилений [Kmod] состояние наблюдателя может быть вычислен, используя различные методы. В этом применении, что касается определения усиления НМУС, принят метод размещения полюса. Важно определить состояния наблюдателя с динамическим быстрее, чем та из вспомогательной системы, увеличивая частоту полюсов. Это позволяет нам получать правильную оценку системы модальные компоненты до желаемой частоты вибрации.
2.4. Схемы управления
Объединяя модального наблюдателя, независимый модальный контроль и оценщика возмущения, очень сильная логика контроля может быть получена. Блок-схему предложенной логики контроля показывают на рис. 1.
Важно указать, что обе стратегии управления могут рассмотреть только небольшое количество системных способов. В частности запоминание ур. (8), матрица ([Ф]T[∧F]T) должна быть обратимой, и это означает, что число рассмотренного (m) способов должно быть равно числу доступных приводных механизмов. В то же время вспомогательная система и наблюдатель могут рассмотреть только небольшое количество системных способов вибрации, чтобы сохранять время вычисления выполнимым для оперативного применения. В любом случае эти соображения в соответствии с общим применением, в котором хорошо определен значительный частотный диапазон, и только небольшое количество способов имеют значительный вклад на динамическую систему.
Так как схема контроля создана на сокращенном количестве способов, его взаимодействие с нерассмотренными способами нужно рассмотреть. Эта тема известна в литературе как избыток [9, 16]. Эта проблема вызывает ухудшение контроля и может привести к системной нестабильности. Было продемонстрировано, что, под предположением о совмещеных датчиков и приводных механизмов, нестабильности избытка можно избежать [17], но во многих заявлениях не может быть удовлетворено это предположение. Так или иначе проблема избытка обычно более важна, когда системные способы не хорошо отделены (что касается примера на пластинах [18]) в то время как подобные лучи структуры как правило хорошо отделяли естественные частоты.

Рис. 1. Блок-схема логики полного контроля

Рис.2. Испытательная установка

Рис. 3. Расположение датчиков на испытательной установки
3. Испытательная буровая установка и числовая модель
Чтобы утвердить иллюстрированную логику, числовая/экспериментальная кампания была выполнена. Система, которую рассматривают, является гибким манипулятором, составленным из трех сегментов, связанных с вращающейся степенью свободы и управляемый гидравлическими приводными устройствами (рис. 2).
Для числового анализа использовалась нелинейная модель FEM манипулятора (см. Касательно [19]). Модель описывает и большое системное движение и маленькие колебания. Модальная оценка состояния выполнена, используя два скоростных датчика, помещенные в наконечник вторых и третьих сегментов (рис. 3). Во время экспериментальной кампании те же самые скорости были получены через интеграцию измерений.
Силы управления с обратной связью, сумма Независимого Модально наблюдателя состояния контроля и волнения, применены к системе посредством тех же самых приводных механизмов, которые выполняют большое движение манипулятора. Так как три приводных механизма доступны на манипуляторе, первые три системных способа рассмотрены для контроля. Таблица 1 показывает естественные частоты и отношения демпфирования, связанные с этими способами для конфигурации манипулятора, представленной на рис. 3.
Положение полюсов и для системы управления, и для модального наблюдателя дано. Усиление НМУС выбрано, используя метод размещения полюса. В этом случае, так как цель контроля - сокращение системной вибрации, системное демпфирование было увеличено до 10%, в то время как естественные частоты не были изменены. Также коэффициент усиления наблюдателя выбран по методу размещения полюса. Так как модальный наблюдатель требует быструю динамику, чем система один, возвратило правильную оценку способа, ее естественные частоты были увеличены, как сообщается в таблице 2. Таким образом наблюдатель состояния следит за системной динамикой без соответствующих задержек. Наконец, таблица 3 показывает коэффициент усиления оценщика волнения, которую рассматривают в числовом и экспериментальном анализе. Более низкий коэффициент усиления принят для более высоких способов, где модальная составляющая оценка менее производительна.
Важно подчеркнуть, что предложенная схема управления строга только для линейных систем, где модальное состояние может быть определено. Так или иначе, для нелинейных систем, модальные подходы управления могут все еще использоваться под определенными предположениями. В частности для продуманной системы нелинейность происходит из-за больших вращений манипулятора. Под предположением о маленькой скорости вращения связи модальный подход можно все еще рассмотреть для управления [19].
4. Числовые и экспериментальные результаты
Первый числовой/экспериментальный анализ был выполнен с фиксированной конфигурацией манипулятора (см. эскиз на рис. 3). Это означает, что, кроме колебаний, манипулятор не изменяет свою конфигурацию и, поэтому, принимая маленькие смещения, его поведение можно считать линейным. Чтобы оценить действия управления, смещение наложено на первый приводной механизм, чтобы моделировать внешнее воздействия. Функция перемещения между данным смещением и ускорением, измеренным на третьем сегменте в определенной конфигурации, оценена с тестом в [0 – 7 Гц] частотном диапазоне. Фиги. 4 и 5 показывают числовое экспериментальное сравнение. В особенности рис. 4 показывает числовые результаты, рассматривая только НМУС (слева) и обе логики контроля (справа). Рис. 5 показывает те же самые результаты, полученные на экспериментальной испытательной буровой установке. Сравнение между Фигами. 4 и 5 шоу очень хорошее соглашение между числовым и
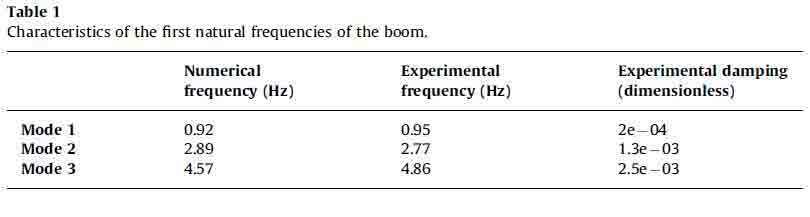

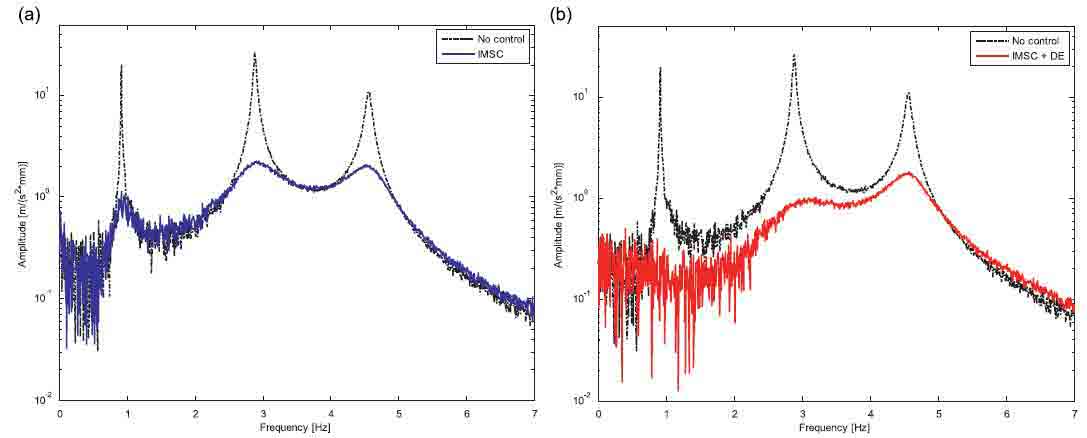
Рис. 4. Численные результаты в линейном случае: сравнение между неуправляемой системой и НМУС. (а) и сравнения между не-управляемой системы и DE(б)
экспериментальные данные в обоих случаях. Можно подчеркнуть, что наблюдатель состояния практически отменить системные колебания, в особенности в низких частотах (ниже 3 Гц).
Было упомянуто ранее, что предложенная логика контроля требует хорошей оценки модальных координат. Качество этой оценки зависит от законности динамической модели системы. Поэтому экспериментальный анализ действий управления переменными системными параметрами был выполнен. В особенности результаты были получены, применяя массу 10 кг к головке стрелы крана (рис. 6), в то время как контроль и параметры наблюдателя были вычислены на оригинальный манипулятор без добавленных масс (таблицы 2 и 3).
Сравнение функции перемещения сообщило в Рисунках. 7 и 5, можно заметить, что в этом случае естественные частоты реальной системы очень отличаются от ожидаемых (см. в особенности второй). Так или иначе и НМУС(Рис. 7a) и НМУС объединили с ОУ (Рис. 7b) шоу хорошее поведение, демонстрирующее значительную надежность даже в присутствии высокого изменения в системе модальных параметров.
Рис. 5. Результаты экспериментов на линейном случае: сравнение между неконтролируемой системой и НМУС (а) и сравнения между неконтролируемой системы и DE (б)

Рис. 6. Испытательный стенд с 10 кг массы, применяемых к наконечнику
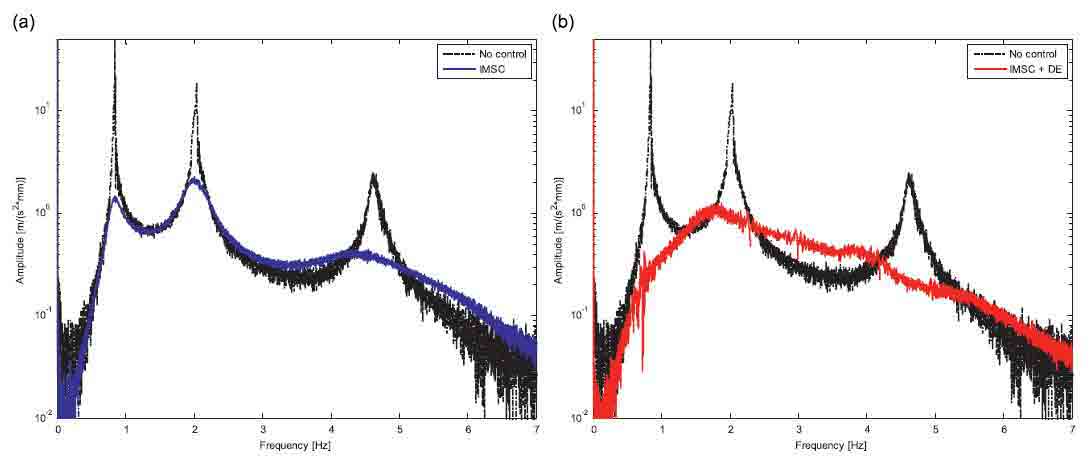
Рис. 7. Экспериментальный анализ прочность: сравнение между системой и неконтролируемой НМУС (а) и между неконтролируемой системы и DE (б)

Рис. 8. Представление большего движения, выполняемого в системе

Рис. 9. Результаты экспериментов на нелинейном случае: сравнение между неконтролируемой системы, НМУС и НМУС + DE
Наконец работа контроля во время большого перемещения была проанализирована. В этом случае, чтобы рассмотреть изменения системных параметров и прибыли во время движения манипулятора. Рис. 8 показывает эскиз большого движения системы, в то время как рис. 9 показывает результаты, используя НМУС только или НМУС и ОУ. Важно указать, что в этом случае движение, наложенное приводными механизмами, действует импульсивная сила на систему. Также в этих условиях эффективность совместного действия НМУС и ОУ может быть замечена. Предложенная логика контроля в состоянии отменить системные колебания даже во время движения приблизительно в половине цикла с существенным улучшением относительно НМУС.