Аннотация
Толочко О.И., Бажутин Д.В. - Модель мостового крану у блоках бібліотеки SimMechanics математичного пакету Matlab. Робота присвячена розробці комп’ютерної моделі мостового крану за допомогою блоків бібліотеки SimMechanics середовища Matlab. Наведено результати моделювання та проаналізовано відповідність наявного математичного опису отриманій моделі.
Вступ.
Кранові установки, виконуючи транспортувальну функцію, є невід’ємною частиною багатьох сучасних виробничих процесів. Суттєвою проблемою при переміщенні вантажів за допомогою крану є виникнення коливань вантажу, які погіршують надійність приводу, енергетичні показники і час транспортування та можуть призводити до аварійних ситуацій. Тому необхідно передбачувати міри щодо гасіння цих коливань.
Одним із засобів гасіння коливань вантажу в мостових кранах є застосовування специфічних тахограм пересування візка або мосту [1, 2, 3, 4]. Всі ці закони виведено на основі спрощеної математичної моделі мостового крану, в якій довжина канату L вважається незмінною.
Мета роботи
Створення математичної моделі, яка б дозволяла дослідити вплив зміни довжини каната мостового крану на коливання вантажу.
Математичний опис процесу пересування візка з вантажем можна отримати з рівняння Лагранжа другого роду. Для системи візок-вантаж формули потенціальної і кінетичної енергії запишуться у вигляді:

де М – маса візка, m – маса вантажу, g – прискорення сил тяжіння, φ – кут відхилення канату від вертикалі, ω(t) – кутова швидкість, vy(t) – швидкість пересування візка, vz(t) – лінійна швидкість намотування каната.
Підставивши ці вирази у формулу функції Лагранжа, при L=const отримаємо такі рівняння руху [1, 2, 3, 4]:
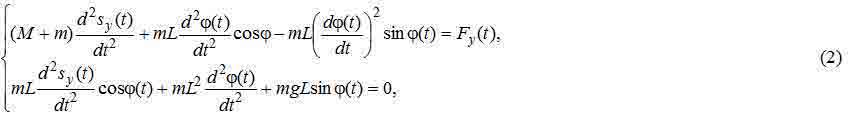
де Fz(t) – зусилля, прикладене до візка із вантажем, sy(t) – лінійне переміщення.
Структурна модель, що відповідає рівнянням (2) наведена, зокрема, в [3].
Математичний опис досліджуваного об‘єкта при L= var можна отримати з рівняння Лагранжа другого роду, підставивши в нього довжину канату як функцію часу. Тоді отримаємо таку систему рівнянь:

де Fy(t) - лінійна сила підйому вантажу. Треба зауважити, що в рівняннях не враховано тертя, яке у дійсності є незначним і його дією можна знехтувати.
Перетворимо їх до системи диференційних рівнянь першого порядку:
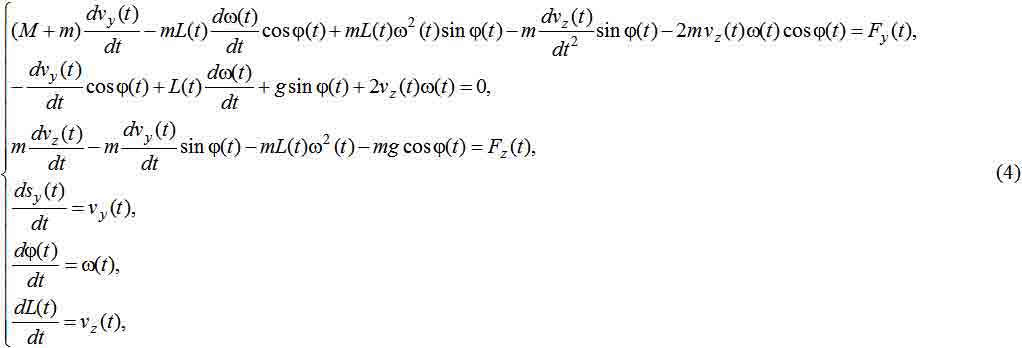
Такій системі рівнянь відповідає структурна модель, наведена на рис.1.
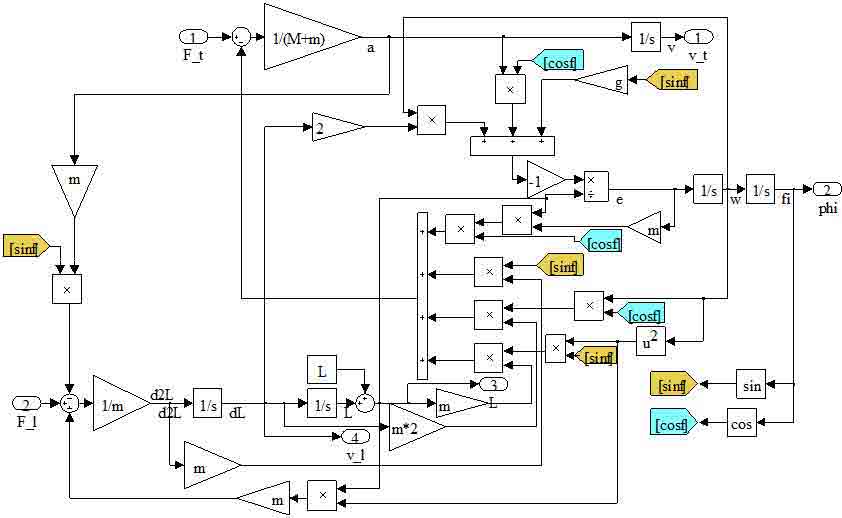
Рисунок 1 – Модель мостового крану у пакеті Matlab/Simulink
Перехідні процеси коливань вантажу при зміні довжини канату та переміщенні візка за трапецеїдальною тахограмою для такої моделі наведено на рис.2. Якість відпрацювання завдання на швидкість за обома каналами керування забезпечується за допомогою двоконтурних систем регулювання швидкості, синтезованих за принципами модульного оптимуму. При цьому для регулятора швидкості візка використовуємо таку структуру регулятора, яка дозволяє повністю компенсувати коливальність об’єкта [3].
Якісні показники перехідних процесів, відображених на рис. 2, відповідають фізичним властивостям об’єкту регулювання. Видно, що частота та амплітуда коливань при зменшенні довжини канату збільшуються. При досягненні бажаної довжини канату в системі спостерігаються усталені коливання, тобто амплітуда і частота залишаються незмінними.
Для перевірки адекватності моделі скористаємось бібліотекою SimMechanics математичного пакету Matlab, яка дозволяє проводити моделювання механічних систем без необхідності виведення їх математичного опису. При цьому модель складається із блоків, що представляють фізичні тіла із заданими геометричними розмірами, заданою масою та матрицею інерції, та блоків, що моделюють різні типи з’єднань об’єктів.
Модель візка мостового крану із підвішеним вантажем наведено на рис.3. Вона складається із таких структурних елементів:
- Середовище моделювання (Machine Environment) – задає напрям дії вектору гравітації, встановлює параметри точності збірки моделі, точність розрахунків.

Рисунок 2 – Перехідні процеси коливань вантажу

Рисунок 3 – Модель візка у блоках бібліотеки SimMechanics
- Візок (Trolley) – моделюється суцільним фізичним тілом із заданою масою, геометричними розмірами та матрицею моментів інерції. До нерухомого мосту кріпиться за допомогою призматичного шарніру (Trolley Drives), через який до візка прикладається момент приводного двигуна.
- Канат (Cable (non-elastic)) – моделюється суцільним негнучким фізичним тілом, вхідними параметрами є довжина, маса та тензор інерції. До візка кріпиться за допомогою телескопічного шарніру (Telescoping), який має три обертових та один поступальний ступінь свободи. Процес намотування канату моделюється шляхом підйому верхньої точки канату відносно точки підвісу. Кут відхилення від вертикалі вимірюється блоком CG Sensor, приєднаного до центру мас канату. особливістю роботи такої системи буде те, що сигнал датчика підйому канату даватиме не абсолютне значення довжини канату, а його зміну. При цьому додатний знак відповідатиме підйому, а від’ємний – опусканню вантажу. Це необхідно враховувати при оцінюванні роботи системи.
- Вантаж (Load) – у найпростішому випадку моделюється у вигляді зосередженої маси, нерухомо приєднаної до канату за допомогою блоку Weld (зварювання).
- Інтерфейсні блоки вводу: F_t – момент приводного двигуна візка, F_l – момент приводного двигуна механізму підйому; та виводу: Vl – швидкість підйому вантажу, dL – зміна довжини канату, V_t – лінійна швидкість візка, phi – кути відхилення вантажу від вертикалі.
Для перевірки адекватності отриманої моделі проведемо моделювання із такими самими сигналами завдання.
Отримані графіки перехідних процесів є цілком ідентичними до отриманих раніше, що свідчить про відповідність двох моделей, а також про адекватність наявного математичного опису реальній системі.
Висновки.
1. Зміна довжини канату під час руху впливає як на рух візка, так і на коливання вантажу. Зменшення довжини призводить до зростання амплітуди і частоти коливань, що в свою чергу збільшує навантаження на приводний двигун візка, як це видно на графіках у вигляді коливань швидкості візка.
2. Бібліотека SimMechanics дозволяє спростити процес створення моделі, оскільки не вимагає наявності математичного опису об’єкта. Важливими є геометричні співвідношення тіл, їх фізичні властивості і форма. Завдяки цьому суттєво спрощується процес уточнення моделі.
3. Отримані моделі можна використовувати для дослідження впливу зміни довжини канату на процес гасіння коливань, а саме встановити, в яких випадках залишковими коливаннями вантажу можна знехтувати, а в яких необхідно застосовувати додаткові заходи.
4.Зміна довжини канату погіршує динаміку системи регулювання швидкості, оскільки коефіцієнти та сталі часу в регуляторах, які залежать від довжини канату, не змінюються у процесі роботи. Це призводить до збільшення помилки регулювання, як це видно на графіках. Метою подальших досліджень може бути адаптивна система регулювання, яка змінюватиме параметри і (або) структуру регулятора в залежності від зміни довжини канату.
Список використаної літератури
- Герасимяк Р.П. Анализ и синтез крановых электромеханических систем – Одесса: СМИЛ, 2008. – 191 с.
- A. Buch. Optimale Bewegungssteuerung von schwingungsfahigen mechatronischen Systemen mit zwei Freiheitsgraden am Beispiel eines Krans mit Pendelnder Last und elastischer Mechanik – Magdeburg, 1999. – 250 S.
- Толочко О.И., Бажутин Д.В. Сравнительный анализ методов гашения колебаний груза, подвешенного к механизму поступательного движения мостового крана / Міжвідомчий науково-технічний журнал «Електромашинобудування та електрообладнання» №75 – Київ: «Техніка», 2010. – С.22-28.
- Толочко О.І., Бажутін Д.В. Обмеження швидкості електропривода візка мостового крану при розгоні у три етапи / Вісник Кременчуцького державного університету імені Михайла Остроградського – Кременчук: КДУ, 2010. – Вип. 4/2010 (63) частина 1. – С. 24-27.