Аннотация
Singhose W., Porter L., Kenison M., Kriikku E. - Effects of hoisting on the input shaping control of gantry cranes The dynamic behavior of a planar gantry crane with hoisting of the load is investigated. The command generation method of input shaping is proposed for reduction of the residual vibration. Several versions of input shaping are evaluated and compared with time-optimal rigid-body commands over a wide range of parameters. Input shaping provides signi"cant reduction in both the residual and transient oscillations, even when the hoisting distance is a large percentage of the cable length. Experimental results from a 15-ton gantry crane at the Savannah River Technology Center are used to support the numerical results.
Abstract
The dynamic behavior of a planar gantry crane with hoisting of the load is investigated. The command generation method of input shaping is proposed for reduction of the residual vibration. Several versions of input shaping are evaluated and compared with time-optimal rigid-body commands over a wide range of parameters. Input shaping provides signi"cant reduction in both the residual and transient oscillations, even when the hoisting distance is a large percentage of the cable length. Experimental results from a 15-ton gantry crane at the Savannah River Technology Center are used to support the numerical results.
1. Introduction
The use of gantry cranes for such applications as handling nuclear waste and loading ship cargoes requires limitation of transient and residual oscillation. If the oscillation of the payload is ignored, time-optimal rigidbody (TORB) commands can be easily calculated. Unfortunately, TORB commands will usually result in large amplitude oscillations. Experienced crane operators attempt to eliminate vibration by causing a deceleration oscillation that cancels the oscillation induced during acceleration, or they may brush the payload against obstacles to damp out the vibration.
When cable swing is considered, the time-optimal flex-body (TOFB) commands that result in zero residual vibration can be generated (Auernig & Troger, 1987; Butler, Honderd & Amerongen, 1991). Hoisting of the load during the motion increases the difficulty of generating the control because the system is nonlinear. If the system model is linearized, then the associated frequency is time-varying. Optimal controls based on a nonlinear model can be difficult to generate (Moustafa & Ebeid, 1988). One method for developing optimal controls divides the motion into fundamental sections. The control for each section is then derived and pieced together (Sakawa& Shindo, 1982). Even when optimal commands can be generated, implementation is usually impractical because the boundary conditions at the end of the maneuver (move length) must be known at the start of the move.
When sensor measurements are available, there are a number of possible feedback control schemes. A combination of open and closed-loop controller has been proposed for rotary cranes (Sato & Sakawa, 1988). An optimal feedback controller has been developed for the general case where there is simultaneous motions of the bridge and trolley, as well as hoisting of the payload (Al-Garni, Moustafa & Nizami, 1995). Several adaptive controllers have been proposed (Butler et al., 1991; Moreno, Acosta, Mendez, Torres, Hamilton & Marichal, 1998; Tanaka & Kouno, 1998). One of these methods uses a neural network to adaptively tune the coefficients of a conventional controller (Moreno et al., 1998). Another of these methods uses an optional parameterlearning method to improve the performance of the controller, which relies on a double-pendulum dynamic model along with sensor measurements of the trolley and payload (Tanaka & Kouno, 1998).
In this paper a control method is proposed for gantry cranes whose frequencies change as the payload is hoisted. The proposed method is easier to derive and implement than the time-optimal control schemes and does not require the feedback mechanisms of closed-loop and adaptive controllers. Unlike most previous command generation methods, the technique used here is very robust to variations in the system parameters. This is demonstrated by investigating its use on a crane that performs hoisting of the load during transverse motions. Rather than attempt to obtain exactly zero residual vibration, which is a practical impossibility, the technique aims for non-zero, but small, levels of vibration.
The control technique investigated here is input shaping - a command generation method that produces a self-canceling command signal. Input shaping is implemented in real time by convolving the command signal with an impulse sequence. The process has the effect of placing zeros near the locations of the flexible poles of the original system. An early form of input shaping was posicast control proposed in the late 1950s (Smith, 1958). More recently, a form of posicast control was successfully applied to the transport of suspended objects (Starr, 1985). Posicast control is based on a simple linear model and is, unfortunately, very sensitive to modeling errors (Singer & Seering, 1990; Tallman & Smith, 1958). When a crane hoists its payload, the system frequency changes; therefore, posicast control will result in some amount of residual vibration.
Robust input shaping techniques have recently been proposed (Singer & Seering, 1990; Singhose, Seering & Singer, 1994) and shown to work effectively on long-reach manipulators (Magee & Book, 1995), as well as on congiguration-dependent systems (Hillsley & Yurkovich, 1993). An IIR filtering technique related to input shaping has been proposed for controlling suspended payloads (Feddema, 1993). Input shaping has been shown to be effective for controlling oscillation of gantry cranes when the load does not undergo hoisting (Noakes & Jansen, 1992; Singer, Singhose & Kriikku, 1997). Experimental results also indicate that shaped commands can be of benefit when the load is hoisted during the motion (Kress, Jansen & Noakes, 1994).
The intent of this paper is to thoroughly investigate the effectiveness of input shaping on gantry cranes when the payload undergoes hoisting. Several types of input shaping schemes are investigated and compared with time-optimal rigid-body commands. An input shaping scheme was implemented on a 15-ton gantry crane, and the experimental results demonstrate the effectiveness predicted by the numerical simulations.
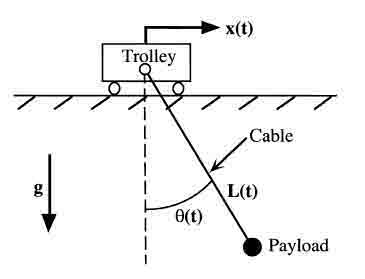
Fig. 1. Model of a planar gantry crane.
2. Model description
The model used for this investigation is shown in Fig. 1. The system is a planar gantry crane with a variable-length cable that simulates hoisting of the payload. The cable is modeled as an inflexible, massless rod that is pinned to the trolley. The configuration of the system is specified by the horizontal position of the trolley, x, the length of the cable, L, and the swing angle of the cable θ. The equation of motion for the system can be written as
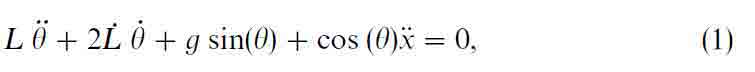
where the acceleration of the trolley, ẍ(t) and the hoisting velocity, Ĺ(t), are considered the control inputs. The trolley position and the cable swing angle are the outputs of interest. The goal under consideration is to change the coordinates x and L, while minimizing θ both during the maneuver and after the move is completed.
3. Time-optimal rigid-body commands
If the oscillatory nature of the payload response is neglected, then time-optimal commands based on the maximum acceleration, αm, and the velocity limit, υm of the system can be calculated. The acceleration commands are bang-bang or bang-off-bang (trapezoidal velocity) if the velocity limit is reached. For the bang-bang region, the command switch time, ts, is

where dx is the move distance. The command is bang-off-bang when dx>υ2m/αm In this case, the duration of the acceleration and deceleration pulses, tp, are

and the coast period between the pulses, tс, is

The above time-optimal rigid-body (TORB) commands are the commands that many inexperienced crane operators would generate when using on-off controls. These commands usually lead to large swing angles. On the other hand, time-optimal flexible-body (TOFB) commands move the system without residual vibration, but they are diffcult to obtain when the load undergoes hoisting. Three additional diffculties occur with TOFB commands: (1) the solution may be sensitive to modeling errors; (2) the command profile must be calculated for each desired maneuver; and (3) implementation on real industrial systems is often impractical.
4. Input shaping
Input shaping limits residual vibration by generating a command profile that tends to cancel its own vibration. That is, the vibration induced by the first part of the command is canceled by vibration induced by a later portion of the command. Input shaping is implemented by convolving a sequence of impulses, an input shaper, with the desired system command. The result of the convolution is then used to drive the system. The input shaping process is demonstrated in Fig. 2. In this example, the desired command is a step input and the input shaper contains three impulses, one of which has a negative amplitude. Note that the rise time of the command has been increased by the duration of the input shaper. The necessary convolution can be computed in real time from signals generated by the crane operator.
The impulses that constitute the input shaper must have appropriate amplitudes and time locations if the shaping process is to reduce vibration. The shaper parameters are determined by solving a set of constraint equations. Several types of input shapers have been proposed (Singer et al., 1997; Singer & Seering, 1990; Singhose et al., 1994; Singhose, Singer & Seering, 1997). This paper evaluates five types of shapers. Two of the shapers are derived from constraints that require zero residual vibration of the flexible mode. The two shapers differ in that one contains only positive impulses, while the other contains a negatively valued impulse that serves to improve the rise time. The two shapers are called the zero-vibration (ZV) shaper and the negative zero-vibration (NEG ZV) shaper. ZV shapers are analogous to posicast control, and they are sensitive to modeling errors and nonlinearities.
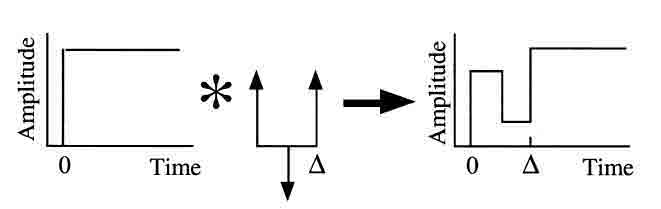
Fig. 2. The input shaping process.
Two additional shapers are considered that use a standard robustness constraint to reduce the sensitivity to modeling errors. Robustness is obtained by setting the derivative of the residual vibration with respect to the frequency equal to zero (Singer & Seering, 1990). These shapers, called the zero vibration and derivative (ZVD) shaper and the negative zero vibration and derivative (NEG ZVD) shaper, keep the residual vibration at a low level even in the presence of modeling errors. To demonstrate this effect, one can plot the residual vibration as a function of the actual system frequency. Fig. 3 shows these curves for both the ZV and ZVD shapers. If the modeling frequency is exact, then both shapers yield zero residual oscillation. However, when modeling errors exist, the ZVD shapers keeps the vibration at a much lower level than the ZV shapers.
The final shaper considered here has a fixed time duration. It is designed by taking the duration as a design parameter and maximizing its robustness to parameter variations (Singer et al., 1997). These specified-duration (SD) shapers have been advocated for use on cranes because the time lag of the shaping process can be tailored to the desires of the human operator. That is, the shaper duration is fixed at a value with which the operator feels comfortable. Note that the shaper duration cannot be made shorter than the time optimal command. The robustness of the input shaper is then maximized to cover as much of the crane workspace as possible.
As an example of the input shaping process, consider the TORB command shown in Fig. 4 that moves the trolley 4 m and hoists the payload 1 m. This command results when the maximum horizontal acceleration and velocity are (αm)x=0.1 m/s2 and (υm)x=0.2 m/s The hoist command is derived assuming (αm)L=0.05 m/s2 and (υm)L=0.1 m/s. The ZV shaper is derived using the frequency of the linearized model at the start of the maneuver (before hoisting changes the frequency). The frequency, ω, is simply  , where g is the acceleration due to gravity and Li is the initial cable length. If the amplitudes of the input shaper impulses are denoted by Ai and the time locations by ti, then the positive ZV
, where g is the acceleration due to gravity and Li is the initial cable length. If the amplitudes of the input shaper impulses are denoted by Ai and the time locations by ti, then the positive ZV

Fig. 3. Sensitivity curves

Fig. 4. Commands for dx = 4 m and dL = - 1 m
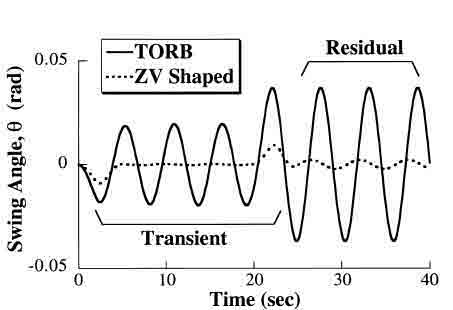
Fig. 5. Swing angle response
shaper for this system is (Singer & Seering, 1990; Smith, 1958)

Note that the amplitudes are dimensionless. When the input shaper is convolved with the original, unshaped command, the resulting command has the same dimensions as the original signal. The command that results from shaping the TORB command with the positive ZV shaper is included in Fig. 4. The cable hoisting command is not shaped because there is no fiexibility in the cable.
Fig. 5 shows the swing angle caused by both the unshaped (TORB) and ZV-shaped commands when Li =8.5 m. Shaping has reduced the residual oscillation amplitude by a factor of 15 and the transient swing by a factor of 3.5. The percentage vibration reduction provided by input shaping is dependent on system parameters, as will be demonstrated in the next section.
Shaping does not reduce the residual oscillation to exactly zero because the system is nonlinear and timevarying. The ZV shaper is designed to eliminate vibration at 0.171 Hz, but by the end of the hoist the frequency changes to 0.182 Hz. The cost of shaping is an increase in command duration. From Fig. 4 it can be seen that the command duration was increased from 22 to 24.92 s. If the negative ZV shaper had been used, the command duration would have been 23.7 s. The time savings of approximately 1 s associated with the NEG ZV shaper is not a large percentage of the total time required for the trolley to travel 4 m. For short moves that take only a few seconds, the percentage improvement with negative shapers would be much larger.
5. Evaluation of input shaping control
The above example demonstrated the usefulness of input shaping for a specific set of parameter values and a single possible maneuver. To obtain an in-depth understanding of the effect of shaping, a wide variety of scenarios must be examined. In this section, the effect will be examined as a function of move distance and hoist distance.
In the previous work, input shaping was compared to time-optimal fiexible-body (TOFB) commands on a linear system with actuator limits (Singhose & Pao, 1997). Input shaping was found to significantly increase robustness to modeling errors, while decreasing system response only slightly. This section compares input shaping to time-optimal rigid-body commands (TORB), rather than to TOFB commands, for two reasons. First, for the wide range of situations examined here, it would be diffcult to calculate the TOFB commands for the nonlinear crane model, especially for cases involving hoisting (Auernig & Troger, 1987). Second, implementation of TOFB commands on real systems may be very challenging, while the use of both TORB commands and input shaping is straightforward. In this sense, it is a more realistic comparison.
The dynamic response of the system to the unshaped TORB commands as well as to the commands shaped with the five shapers discussed in the previous section was simulated. For certain parameter ranges (very short duration moves compared to the oscillation period), the negative shapers lead to shaped commands that exceed the acceleration limit (Singhose et al., 1997). Only data for physically realizable inputs will be shown.
5.1. No hoisting
The results shown here were obtained by varying the parameters of a system that has the following baseline parameters: (αm)x=0.1 m/s2, (υm)x=0.2 m/s, (αm)L=0.05 m/s2, (υm)L=0.1 m/s and Li=8.5 m Fig. 6 shows the amplitude of residual oscillation when the move distance is varied from 1 to 10 m and no hoisting is performed (dL=0). All types of shapers yield nearly zero residual vibration. The SD shaping does not require zero vibration, as do the other shapers, but rather limits the vibration to a small percentage of that resulting from the TORB commands. Consequently, while the TORB commands generate up to 0.036 rad of residual swing (61 cm peak-to-peak residual oscillation), the SD shaping causes less than 0.0018 rad (5% of 0.036) of swing. The nonrobust ZV input shaping is effective over this large parameter range because no hoisting of the load occurs.
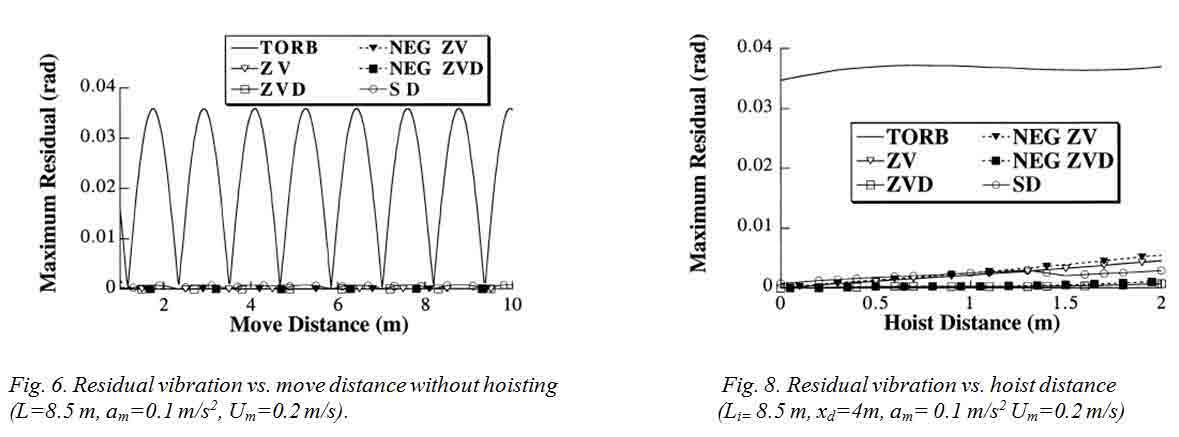
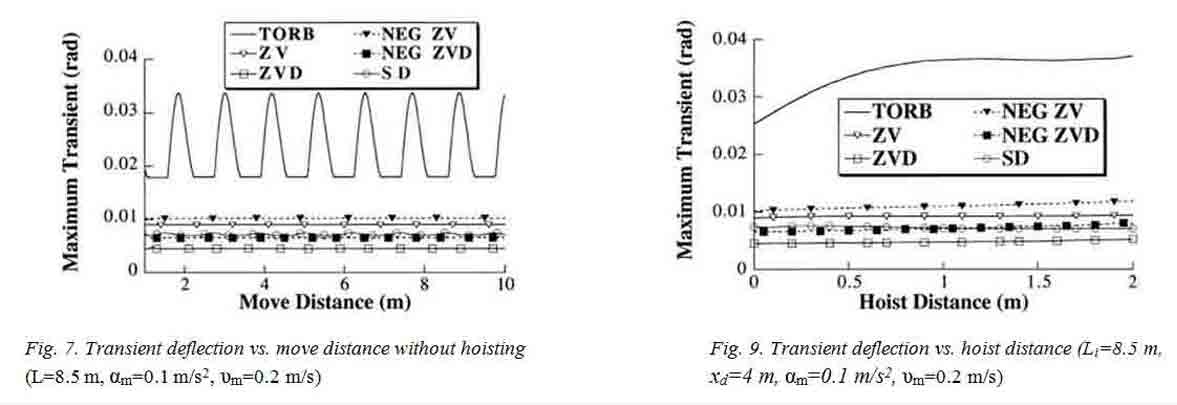
Fig. 7 compares the maximum transient swing angles. The transient swing is limited to about 0.005 rad with ZVD shaping and to about 0.009 rad with ZV shaping. The negative shapers cause slightly more transient swing than the positive shapers. The SD shaper transient most closely resembles the transient amplitudes with the negative ZVD shaper, generating up to 0.0075 rad of transient swing. The TORB commands cause larger transients that vary between 0.018 and 0.034 rad.
5.2. Hoisting during the motion
Fig. 8 shows the residual vibration amplitude when the move distance is held constant at 4 m and hoisting occurs. The shapers are designed for the initial cable length of 8.5 m. The move distance and initial length values were chosen because they are typical parameters for a crane from which experimental data was obtained. As the hoist distance increases, the residual oscillations with shaping increase. However, even when the hoist distance is 24% of the initial cable length (2 m), the ZV shaping reduces the amplitude of residual oscillations to about 12% of that resulting from the TORB commands. The ZVD shaping works considerably better; the residual oscillation remains below 2% of the TORB level for all hoist distances. The SD shaping is also very effective, keeping the residual oscillation to below 8% of the TORB level.
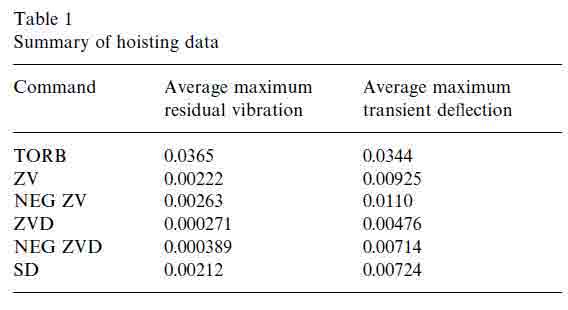
Fig. 9 shows the maximum transient deflection corresponding to the runs shown in Fig. 8. The transient with negative ZV shaping averages 32% of the TORB deflection, while the positive ZV averages 27%. The transient deflections with SD and NEG ZVD shapers are similar and are about 21% of the TORB deflection, while those of the positive ZVD are about 14% of the TORB values. Regardless of the type of shaper used, maximum transient deflection depends very little on hoist distance.

Table 1 summarizes the above results by showing the average maximum residual vibration amplitude and transient deflection over the range of hoist distances.
Figs. 8 and 9 show the results when the shaper is designed for the initial frequency of the system. Somewhat better results can be obtained by using a shaper designed for an “averagea” frequency. Two averaging schemes were investigated. The first scheme uses the average of the initial frequency (the frequency before hoisting) and the final frequency (the frequency when hoisting has been completed). The second method uses the frequency corresponding to the average cable length; i.e., if the initial length is 8.5 m and a 2 m hoist is performed, then the frequency corresponding to 7.5 m is used. Because frequency does not vary linearly with cable length, these two averaging schemes are not equivalent; however, for the hoist distances examined in this paper, they yield similar values. Hence, the two averaging schemes resulted in comparable reductions in residual vibration, as seen in Fig. 10. Also shown in Fig. 10 for comparison are the results from Fig. 8, where the shaper was designed for the initial length of 8.5 m. Clearly, both averaging schemes improve performance considerably. Note, however, that the use of either averaging scheme requires knowledge of how far the payload will be hoisted.
6. Experimental results
To verify the results of the previous section, experiments were performed on a 15-ton gantry crane at the Savannah River Technology Center (SRTC). The crane bridge travel is 85 ft, the trolley travel is 43 ft, and the vertical hook travel is 29 ft. The specified-duration (SD) input shaper used to modify commands generated by the human operator was
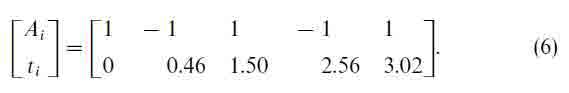
To examine the effect of hoisting, the crane was repeatedly moved a horizontal distance of 3.9 m. During each motion, the hoist distance was varied, and the residual oscillation amplitude was recorded. Fig. 11 compares the experimentally obtained residual vibration to the theoretical results. The experimental data compare very well with the values predicted by the numerical model. The effectiveness of the SD shaping in the presence of hoisting is readily apparent from Fig. 11. The residual oscillation is reduced by a factor of 20}30 over the range of hoist distances shown.
7. Conclusions
Input shaping was shown to significantly reduce the residual swing of a gantry crane when the payload is hoisted. Input shaping does not yield exactly zero residual vibration; however, when the hoist distance is small, the method yields essentially zero residual vibration. Even when hoist distances are large, the shaping process reduces residual oscillation amplitude well below the level obtained with time-optimal rigid-body commands. Input shaping also greatly reduces transient swing. In general, input shapers designed using the average operating frequency are more effective than shapers based on the initial frequency. Experimental results from a 15-ton gantry crane support the findings of the numerical simulations.
References
- Al-Garni, A. Z., Moustafa, K. A. F., & Nizami, S. S. A. K. J. (1995). Optimal control of overhead cranes. Control Engineering Practice, 3, 1277-1284
- Auernig, J. W. & Troger, H. (1987). Time optimal control of overhead cranes with hoisting of the load. Automatica, 23, 437-446
- Hillsley, K. L., & Yurkovich, S. (1993). Vibration control of a two-link fiexible robot arm. Journal of Dynamics and Control, 3, 261-280
- Kress, R. L., Jansen, J. F. & Noakes, M. W. (1994). Experimental implementation of a robust damped-oscillation control algorithm on a full sized, two-DOF, AC induction motor-driven crane, Fifth ISRAM, Maui, HA, pp. 585-92
- Magee, D. P. & Book, W. J., (1995). Filtering micro-manipulator wrist commands to prevent fiexible base motion. American control conference, Seattle, WA (pp. 924-928)
- Moreno, L., Acosta, L., Mendez, J. A., Torres, S., Hamilton, A. & Marichal, G. N. (1998). A self-tuning neuromorphic controller: Application to the crane problem. Control Engineering Practice, 6, 1475-1483
- Moustafa, K. A. F., & Ebeid, A. M. (1988). Nonlinear modeling and control of overhead crane load sway. Transactions of the ASME, 110, 266-271
- Noakes, M. W., & Jansen, J. F. (1992). Generalized inputs for dampedvibration control of suspended payloads. Robotics and Autonomous Systems, 10, 199-205
- Sakawa, Y., & Shindo, Y. (1982). Optimal control of container cranes. Automatica, 18, 257-266
- Sato, K., & Sakawa, Y. (1988). Modeling and control of a fiexible rotary crane. International Journal of Control, 48, 2085-2105
- Singer, N., Singhose, W. & Kriikku, E. (1997). An input shaping controller enabling cranes to move without sway. In ANS seventh topical meeting on robotics and remote systems, Augusta, GA
- Singer, N. C., & Seering, W. P. (1990). Preshaping command inputs to reduce system vibration. Journal of Dynamic Systems, Measurement, and Control, 112, 76-82
- Singhose, W., & Pao, L. (1997). A comparison of input shaping and time-optimal #exible-body control. Control Engineering Practice, 5, 459-467
- Singhose, W., Seering, W., & Singer, N. (1994). Residual vibration reduction using vector diagrams to generate shaped inputs. Journal of Mechanical Design, 116, 654-659
- Singhose, W., Singer, N., & Seering, W. (1997). Time-optimal negative input shapers. Journal of Dynamic Systems, Measurement, and Control, 119, 198-205
- Smith, O. J. M. (1958). Feedback control systems. New York: McGraw-Hill
- Starr, G. P. (1985). Swing-free transport of suspended objects with a path-controlled robot manipulator. Journal of Dynamic Systems, Measurement and Control, 107, 97-100
- Tallman, G. H., & Smith, O. J. M. (1958). Analog study of dead-beat posicast control. IRE Transactions on Automatic Control, 14-21
- Tanaka, S., & Kouno, S. (1998). Automatic measurement and control of the attitude of crane lifters. Control Engineering Practice, 6, 1099-1107