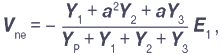
Автор: Gernot Druml, компания Aeberle GmbH, Нюрнберг, Германия; Andreas Kugi, университет Кеплера, Линц, Австрия; Bodo Parr, компания Aeberle GmbH, Нюрнберг, Германия.
Основная причина снижения уровня напряжения естественной несимметрии состоит в том, что уменьшаются отклонения в параметрах (емкостях на землю) новых однофазных кабелей. Кроме того, в кабельной изоляции активные потери меньше по сравнению с воздушными линиями. Вследствие этого затухание сетей (демпфирование) снижается и резонансные кривые становятся более заостренными.
Для удовлетворения таких новых требований в отношении управления дугогасящими реакторами 6–35 кВ, очевидным решением является увеличение чувствительности измерения напряжения на нейтрали. Однако ниже будет показано, что использование такого подхода не позволяет получить удовлетворительные результаты. Основная причина этого заключается в том, что возмущения, создаваемые, например, несимметричным расположением кабелей, выше, чем помехи измерения.
На рис. 1 показана упрощенная схема замещения сети 6–35 кВс идеальным симметричным источником трехфазного напряжения.
Для получения математической модели сделаны следующие допущения (см. рис. 1): емкости и активные проводимости между фазами и землей равны; небаланс (емкостный С и активный G) присутствует только в фазе 1.
Для схемы рис. 1 справедливы следующие уравнения:
IР + I1 + I2 + I3 = 0, (1)
VnеYР = IР, (2)
(E1 + Vne)Y1 = I1, (3)
(E2 + Vne)Y2 = I2, (4)
(E3 + Vne)Y3 = I3, (5)
Полные проводимости можно записать в виде:
YР = GР + 1 / jwLР, (6)
Y1 = (G + DG)+ jw(C + DC), (7)
Y2 = Y3 = G + jwC, (8)
Считая систему фазных напряжений симметричной и используя сокращение а = е–j120 при 1 + а + а2 = 0, можно записать напряжения Е2 и Е3 в следующей форме:
Е2 = а2Е1 и Е3 = аЕ1. (9)
Уравнение (1) можно переписать в виде:
Vne(YР + Y1 + Y2 + Y3) + E1(Y1 + a2Y2 + aY3) = 0 (10)
или эквивалентно:
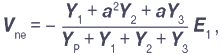
Используя (6–8), получаем:
Y1 + a2Y2 + aY3 = G + jwDC, (12)
Y1 + Y2 + Y3 = (3G + DG) + jw(3C + DC). (13)
Из (11) можно получить уравнение:
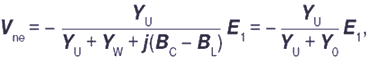
где YU=G+jwDC – проводимость в месте повреждения;
YW=3G+GР – активная составляющая проводимости нулевой последовательности Y0;
BC=3wC – емкостная составляющая проводимости нулевой последовательности Y0;
BL=1/wLP – индуктивная составляющая проводимости нулевой последовательности Y0.
Эквивалентная схема по (14) представлена на рис. 2. Она справедлива для однофазных замыканий через малое сопротивление в месте повреждения, а также для естественного емкостного небаланса в исправной сети (с учетом допущений).
В случае однофазного замыкания через малое активное сопротивление RF 0 емкостным небалансом jwDC можно пренебречь (активная проводимость DG=1/RF достаточно высока). При этих условиях напряжение на нейтрали Vne постоянно (см. рис. 2, где в этом случае YU ) и равно фазному напряжению сети. На рис. 3 показана зависимость абсолютного значения тока в месте замыкания IF от тока компенсации дугогасящего реактора для сети напряжением 20 кВ (IC = BCE1 = 150 A, IW = YWE1 = 5 А, 1 / YU = 1 Ом).
При отсутствии в сети замыкания активная проводимость G незначительна по сравнению с емкостным небалансом jwDC сети. Вследствие этого ток IF более или менее постоянен (см. рис. 2). На рис. 4 показана зависимость абсолютного значения напряжения на нейтрали Vne (в % по отношению к фазному напряжению) от значения тока компенсации дугогасящего реактора для сети 20 кВ (IC = BCE1 = 150 A, IW = YWE1 = 5 A и 1 / YU = 40 кОм).
Резонансная кривая исправной сети (рис. 4) может быть описана следующими тремя параметрами:
Vres – максимальное напряжение резонансной кривой;
Ires – соответствующее положение тока дугогасящего реактора при Vres;
IW – активный остаточный ток в месте повреждения при однофазном замыкании через пренебрежимо малое сопротивление.
Эти параметры можно легко определить по резонансной кривой. В точке резонанса (BC = BL) уравнение (14) упрощается до:
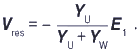
Для того чтобы объяснить значения параметра IW, рассмотрим точку резонансной кривой рис. 4, в которой справедливо соотношение:
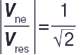
При допущении, что YU << YW, соответствующее положение реактора Ipos, W = BL,WE1 может быть вычислено по уравнению (14) в форме:
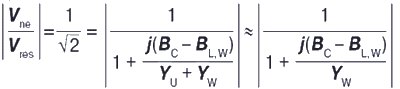
или эквивалентно:
(BC – BL,W) = YW. (17)
Умножая (17) на E1, получаем соотношения:
(BC – BL,W)E1 = Ires – Ipos,W = YWE1 = IW. (18)
(BC – BL,W)E1 = Ires – Ipos,W = YWE1 = IW. (18) Таким образом, из (18) следует, что разница между положением реактора в точке резонанса Ires и положением
катушки Ipos,W, где напряжение равняется активному остаточному току IW.
Для объяснения улучшенного алгоритма управления рассмотрим абсолютное значение инвертированного напряжения на нейтрали:
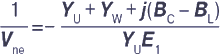
На рис. 5 представлена зависимость абсолютного значения инвертированного напряжения на нейтрали 1/Vne (в %) от тока компенсации ДГР.
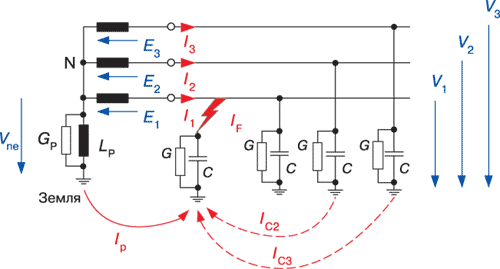
Рис. 1. Упрощенная схема замещения сети с дугогасящим реактором и поперечной несимметрией в одной из фаз
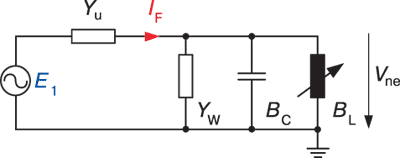
Рис. 2. Однофазная эквивалентная схема
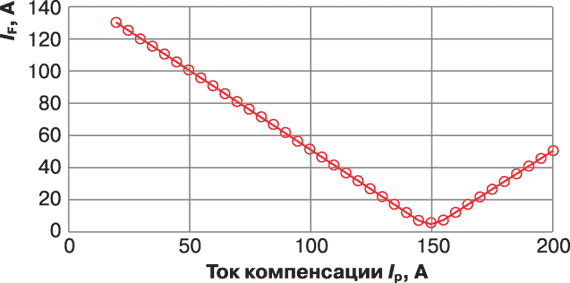
Рис. 3. Зависимость абсолютного значения тока в месте замыкания IF от тока компенсации дугогасящего реактора
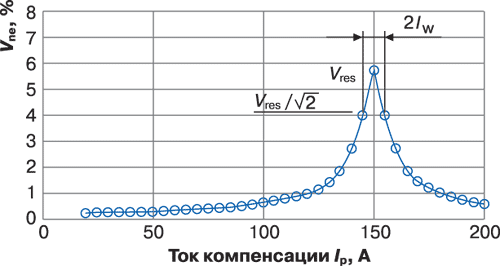
Рис. 4. Зависимость абсолютного значения напряжения на нейтрали от значения тока компенсации дугогасящего реактора в отсутствие замыкания
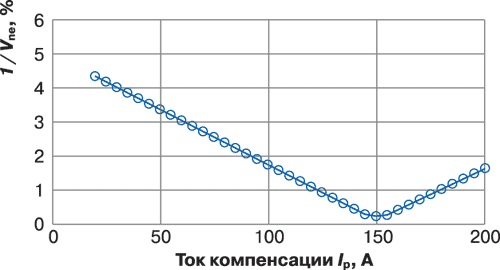
Рис. 5. Зависимость абсолютного значения инвертированного напряжения на нейтрали от тока компенсации дугогасящего реактора
Из изложенного выше следует, что найти резонансную точку исправной сети достаточно просто даже в случае очень малого напряжения на нейтрали Vne. Однако нахождение резонансной точки осложняется рядом помех в напряжении на нейтрали Vne, которые затрудняют определение реальной резонансной точки и мнимых.
Существуют различные причины возникновения помех при измерении напряжения на нейтрали Vne:
1. Высокие уровни помех при измерениях Vne вследствие индуктивных и емкостных наводок на цепь связи измерительной обмотки ДГР и регулятора. Это влияние может быть уменьшено путем использования витых и экранированных измерительных цепей.
2. Разрешающая способность аналогоцифрового преобразователя. Резонансный максимум в кабельных сетях часто меньше 0,5% фазного напряжения E1. Таким образом, для того чтобы определить резонансную кривую, разрешение измерений должно быть в диапазоне 0,01% от E1.
3. Гармоники в системе нулевой последовательности. Они могут быть отфильтрованы в регуляторе.
4. Небаланс напряжения (dE1) изза влияния сети высокого напряжения.
5. Небаланс напряжения (dE1) по причине производственных допусков понижающего силового трансформатора в диапазоне менее 1%. В результате этого полностью симметричная система напряжений на стороне высокого напряжения трансформатора создает несимметричную систему напряжений на стороне среднего напряжения.
6. Асимметричная нагрузка собственных нужд подстанции на третичной обмотке заземляющего трансформатора (зигзаг) также создает небаланс напряжения (dE1).
7. Небаланс емкостей на землю разных фаз вследствие разного геометрического расположения фаз на воздушных линиях или же вследствие производственных допусков при изготовлении кабелей.
8. Связь тока нагрузки через малые активные и реактивные сопротивления линии (симметричные и несимметричные величины).
9. Связь тока нагрузки через взаимные реактивные сопротивления линий (симметричные и несимметричные величины).
10. Измерение напряжения на нейтрали Vne с использованием собранных в разомкнутый треугольник обмоток измерительного ТН на шинах подстанции вместо вспомогательной обмотки ДГР приводит к постоянной ошибке по амплитуде и фазе измеряемого напряжения.
11. Нелинейность связи между измеренным положением дугогасящего реактора и его реальной индуктивностью. Датчик положения реактора – это линейный потенциометр, который выдает сигнал, пропорциональный воздушному зазору. Однако индуктивность дугогасящего реактора является слабо нелинейной функцией воздушного зазора.
12. Емкостная связь параллельных линий разного напряжения, расположенных на одних и тех же опорах.
Для анализа влияния возмущений по пунктам 4-9 рассмотрим сеть 20 кВ (рис. 6). Источники помех могут быть сведены к небалансу напряжения (dE1); небалансу фазных емкостей на землю;к связи тока нагрузки через незначительные активные сопротивления и реактансы линии.
С учетом допущения того, что все компоненты сети симметричны, кроме несбалансированного напряжения dE1, получаем следующее соотношение между Vne и dE1:
где:
– полная продольная проводимость линии; YC = jwC – емкостная проводимость на землю;
– полная проводимость дугогасящего реактора.
Важное содержание уравнения (20) состоит в том, что даже в сети с идеально симметричными компонентами (сопротивления линий, взаимные сопротивления, емкости на землю и нагрузки) небаланс dE1 создаст напряжение на нейтрали Vne, не равное нулю. Кроме этого, амплитуда напряжения на нейтрали зависит от различных параметров сети и имеет максимум в том случае, когда дугогасящий реактор настроен в резонанс. Зависимость |Vne / dE1| от тока компенсации дугогасящего реактора в сети по рис. 6 показана на рис. 7.
Для упрощения предположим, что dE1 = 0 и имеется небаланс DYС в емкости только фазы 1. Следующее соотношение:
может быть найдено с помощью
Yn1 = (YC +YL +Yнагр. + DYC) · (3YLYC + YP(YL + YC)), (22)
Yn2 = DYC(3YL2 + Yнагр.(YP +3YL)),
Yнагр. = 1 / Zнагр.,
DYC = jwDC.
Естественный небаланс емкостей относительно земли DYC вызывает появление напряжения на нейтрали Vne, не равного нулю. Но теперь Vne также зависит от нагрузки Yнагр. и, следовательно, от тока нагрузки, протекающего через продольные сопротивления линии. Как видно из (21) и (22), эта зависимость присутствует даже тогда, когда последовательные сопротивления линии и нагрузка симметричны. На рис. 8 показана зависимость |Vne / E1| от тока нагрузки в случае настройки дугогасящего реактора в резонанс для сети по рис. 6.
Примем, что небаланс dE1 = 0 и сеть симметрична, кроме несимметрии 5% в продольном сопротивлении ZL фазы 1. Математические зависимости в данном случае достаточно сложны. Зависимость напряжения на нейтрали |Vne / E1| от тока нагрузки при продольной несимметрии параметров линии при настройке дугогасящего реактора в резонанс показана на рис. 9.
Как видно из рис. 9, имеет место увеличение напряжения на нейтрали Vne при росте тока нагрузки. Если ток нагрузки равен нулю, то напряжение Vne определяется небалансом емкостей на землю. Взаимосвязанные напряжения емкостного небаланса и небаланса продольных сопротивлений в линиях компенсируют друг друга. Но напряжение на нейтрали возрастает при росте нагрузки.
Продольная несимметрия параметров линии может быть связана со способом прокладки кабеля. Если кабели расположены треугольником, то взаимные сопротивления фаз, очевидно, будут одинаковы.
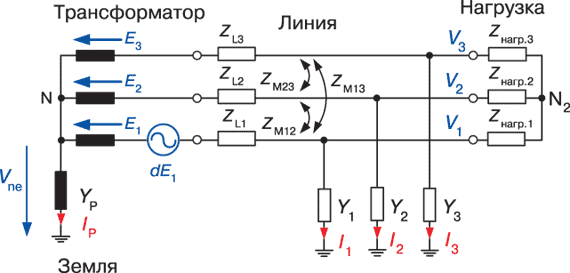
Рис. 6. Упрощенная эквивалентная схема для анализа небалансов при измерении напряжения на нейтрали
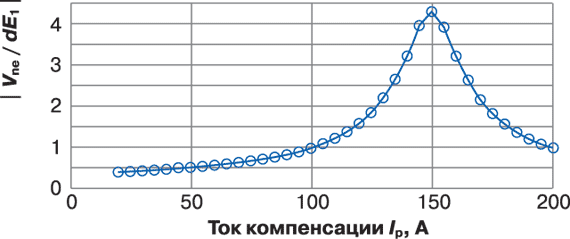
Рис. 7. Зависимость |Vne / dE1| от тока компенсации дугогасящего реактора
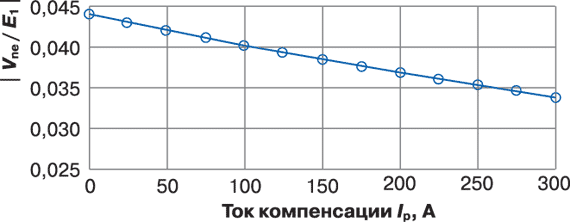
Рис. 8. Зависимость |Vne / E1| от тока нагрузки при настройке дугогасящего реактора в резонанс и небалансе емкостей фаз на землю
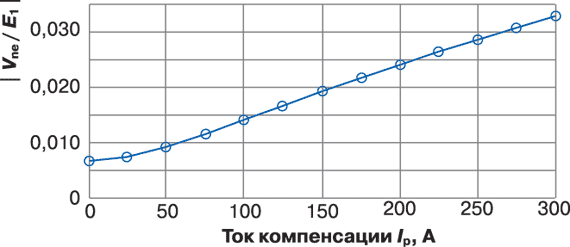
Рис. 9. Зависимость |Vne / E1| от тока нагрузки при продольной несимметрии параметров линии и настройке дугогасящего реактора в резонанс
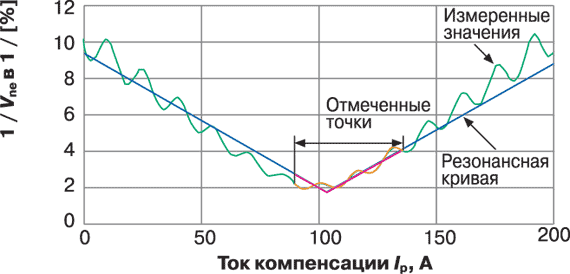
Рис. 10. Инвертированная резонансная кривая на основе выбранных значений
Количественные величины, которые измеряет регулятор реактора, это ток реактора Ip и напряжение на нейтрали Vne.
Задача регулятора состоит в том, чтобы обнаружить изменение конфигурации сети и настроить дугогасящий реактор на новую точку резонанса или с заранее заданной перекомпенсацией. В простейшем случае изменение абсолютного значения напряжения на нейтрали Vne используется как сигнал возникновения изменения сети. Однако при таком подходе не все изменения сети могут быть обнаружены. Улучшить это можно за счет анализа изменения напряжения на нейтрали Vne в комплексной плоскости. Для вычисления параметров резонансной кривой сети необходимо изменить настройку дугогасящего реактора и измерить соответствующее изменение напряжения на нейтрали.
Как было показано выше, напряжение на нейтрали искажается различными помехами. Для правильной настройки ДГР регулятор должен:
различать подлинную резонансную точку и ложные точки резонанса при малом напряжении естественной несимметрии на нейтрали;
распознавать коммутационные операции в сети при настройке дугогасящего реактора.
Используя метод наименьших квадратов, параметры Vne, Ires и IW резонансной кривой (рис. 4) можно получить с достаточной надежностью.
ДГР требуется приблизительно 60 с для перемещения плунжера от одного концевого выключателя до другого. Поэтому необходимо, чтобы во время операции настройки имелась возможность осуществлять новую оценку каждые 0,5 с. Во избежание слишком больших затрат на вычисления задача оценки нелинейных параметров заменяется на линейную задачу. С этой целью рассмотрим уравнение (19) в форме:
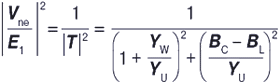
где
x1 = BC; (26)
x2 = YU2; (27)
x3 = YU2 + 2YUYW + YW2 + BC2. (28)
Уравнение (25) можно решить с помощью классического метода наименьших квадратов, чтобы получить BC, YU, YW и на этой основе параметры Vres, Ires и IW для построения резонансной кривой.
Рассмотренный выше улучшенный алгоритм управления ДГР был реализован в цифровом регуляторе REGDP и продемонстрировал свои преимущества в реальных сетях среднего напряжения. На рис. 10 представлена инвертированная резонансная кривая, полученная на основе расчета параметров кривой только по отмеченным точкам из всего массива измеренных значений.
Реальная резонансная точка сети соответствует току 100 А. Полученная точность достаточна для настройки реактора в резонанс.
ВЫВОДЫ
На основе проведенных исследований разработан улучшенный алгоритм управления дугогасящими реакторами 6–35 кВ, обеспечивающий высокую точность настройки и низкую восприимчивость к различным небалансам и возмущениям, имеющим место в реальных условиях эксплуатации. Испытания в реальных сетях среднего напряжения продемонстрировали эффективность алгоритма в отношении управления дугогасящими реакторами 6–35 кВ.
Источник: news.elteh.ru