Для схем содержащих только два узла или приводящихся к ним, применяют метод двух узлов. Схема расмотреная в данном задании имеет вид представленный на рисунке 1.
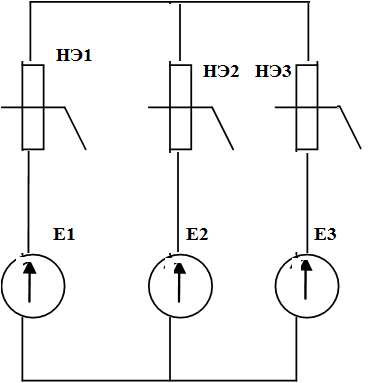
Рисунок 1 – Схема расмотреная для примера.
По заданию мы имеем три нелинейных элемента заданных таблично. При помощи клавиатуры вводим параметры в программу.
U1 = [0 5 10 15 20 25 30 35 40 45];
I1 = [0 1.2 1.4 1.8 2 3 4 5 5.1 5.2];
U2 = [0 5 10 15 20 25 30 35 40 45];
I2 = [-4 -3.8 -2 0 1 2 4 6 6.1 6.2];
U3 = [0 5 10 15 20 25 30 35 40 45];
I3 = [0 3 3.25 3.75 4.01 5 5.05 5.1 5.5 5.5];
Далее для наглядности мы можем просмотреть вольт-амперные характеристики каждого элемента. Для удобства ВАХ имеют различные цвета. В случае параметров указанных выше мы имеем ВАХ показанные на рисунке 2.
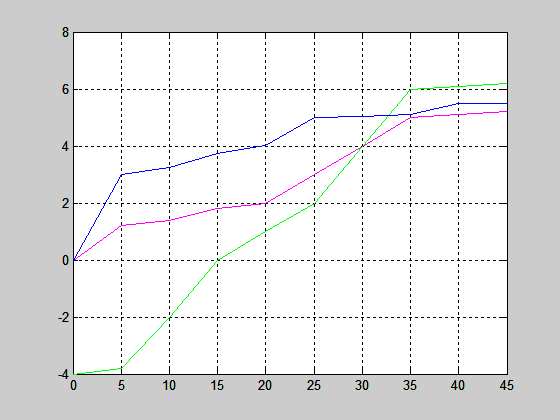
Рисунок 2 – ВАХ нелинейных элементов.
Также каждая ВАХ представлена в виде степенного полинома:
V1= polyfit(U1,I1,8)
VAX1 = poly2str(V1,'x')
V2= polyfit(U2,I2,8)
VAX2 = poly2str(V2,'x')
V3= polyfit(U3,I3,8)
VAX3 = poly2str(V3,'x')
VAX1 = -1.0476e-010 x^8 + 2.0702e-008 x^7 - 1.6539e-006 x^6 + 6.8846e-005 x^5 - 0.0016156 x^4 + 0.02182 x^3 - 0.16456 x^2 + 0.67939 x + 0.00084122
VAX2 = -1.2381e-010 x^8 + 2.9046e-008 x^7 - 2.608e-006 x^6 + 0.00011562 x^5 - 0.0026699 x^4 + 0.030219 x^3 - 0.12582 x^2 + 0.18282 x – 4
VAX3 = -2.3048e-010 x^8 + 4.0071e-008 x^7 - 2.8832e-006 x^6 + 0.00011229 x^5 - 0.0026061 x^4 + 0.037203 x^3 - 0.31762 x^2 + 1.5193 x + 0.0013398
Используя второй закон Кирхгофа имеем:
Uab1=E1-U1
Uab2=E2-U2
Uab3=E3-U3
По напряжению Uаб строим вольт-амперные характеристики.
figure (2)
plot(Uab1,I1,'k')
hold on
plot(Uab2,I2,'g')
plot(Uab3,I3,'y')
Находим результирующий ток: Iр=I1+I2+I3 и в этой же системе координат строим результирующую ВАХ. Согласно первому закону Кирхгофа Iр=0, что является точкой пересечения результирующей ВАХ с осью абцис. Далее проведя вертикальную линию параллельную оси ординат и проходящую через точку пересечения мы определяем соответствующие токи в ветвях как это показано на рисунке 3.

Рисунок 3 – График для определения тока в ветвях
Как видно с графика I1=1А, I2=-4А, I3=3А.