ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННЫХ ТАБЛИЦ ДЛЯ РЕШЕНИЯ МАТЕМАТИЧЕСКИХ И ИНЖЕНЕРНЫХ ЛЭП
Л.Г. Черная, Е.Р. Алексеев
Донецкий национальный технический университет
Целью данной работы является сравнение возможностей электронных таблиц (Microsoft Office Excel, Gnumeric, OpenOffice .org Calc) для решения математических и инженерных задач.
The purpose of this article is to compare the capabilities of spreadsheets (Microsoft Office Excel, Gnumeric, OpenOffice.org Calc) in solving of mathematical and engineering problems.
Дана стаття написана з метою порівняння можливостей електронних таблиць (Microsoft Office Excel, Gnumeric, OpenOffice.org Calc) задля вирішення математичних й інженерних задач.
В работе рассмотрены возможности электронных таблиц для решения математических и инженерных задач.
При решении практических задач многие исходные данные и результаты удобно демонстрировать графически. Поэтому возможность построения различного вида графиков и диаграмм является важным показателем для выбора инструмента для решения поставленных задач. Таблицы MS Excel, OpenCalc и Gnumeric дают возможность пользователю построить различные графики, среди которых: точечный, график в полярной системе координат, график поверхности (трехмерный график). Существует возможность изобразить графики нескольких функций в одной системе координат. Все рассматриваемые табличные процессоры позволяют строить диаграммы. Стоит отметить, что возможности OpenCalc при построении трехмерных графиков очень ограничены. Кроме того, обращают на себя внимание мощные инструменты импорта и экспорта графических файлов в Gnumeric1.
Рассмотрим процесс построения графиков (диаграмм) в Calc, так как он значительно отличается от двух других табличных процессоров. Пункт Диаграмма из меню Вставка и Мастер диаграмм позволяют пройти по всем шагам этого процесса. Сначала необходимо выделить область данных, щелкнуть по Мастеру диаграмм, на экране появится диалоговое окно первого шага мастера диаграмм (рис. 1). Следует обратить внимание на то, что при расположении исходных данных построчно, первый столбец в таблице будет содержать названия легенд, первая строка — числовые данные, которые наносятся на ось абсцисс, а второй строка и последующие – это массивы ординат для построения соответствующего графика. Если данные расположены по столбцам, то в первой строке будут легенды, а столбцы будут содержать числовые данные для построения графиков [4].
На следующем шаге мастера диаграмм (рис. 2) можно изменить область для построения графика и определить, как располагаются данные: по строкам или по столбцам.
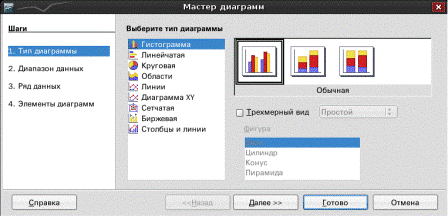
Рис. 1.
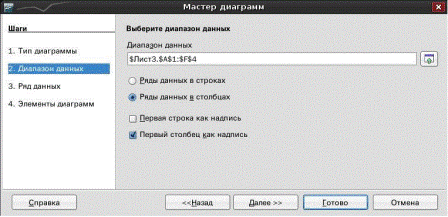
Рис. 2.
Изменить исходные данные для конкретного ряда можно на третьем шаге (рис. 3). Здесь же можно определить имя легенды (поле Диапазон для: Название). На
заключительном, четвертом шаге Мастера диаграмм необходимо определить параметры диаграммы: заголовки, подписи осей, свойства легенды (рис. 4).
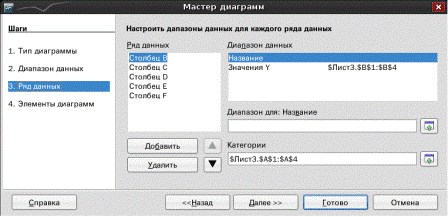
Рис. 3.
Рис. 4.
После создания диаграммы в табличном процессоре можно изменить ее размер, переместить, изменить любой ее элемент. Редактировать и модифицировать диаграмму можно как непосредственно на листе, так и с помощью меню.
Перед редактированием диаграммы ее необходимо выделить. Для этого достаточно щелкнуть по ней. Вокруг диаграммы появятся маркеры и можно перетащить диаграмму в иное место рабочего листа, а для изменения ее размера необходимо подвести курсор к маркеру. Курсор мыши изменит вид и, нажав левую кнопку мыши, можно изменять размер. Существует возможность редактировать все элементы непосредственно на диаграмме. Для этого необходимо только щелкнуть на нужном элементе или области, появится меню и процесс редактирования можно начинать.
Для того, чтобы добавить или удалить ряд данных на диаграмме необходимо: выделить на диаграмме данные, щелкнуть правой кнопкой мышки
и выбрать команду Диапазоны данных.
Появится окно Мастера диаграмм. Оно имеет две закладки Диапазоны данных и Ряд данных. В этом окне можно добавлять новые ряды данных (кнопка Добавить)
и удалять уже существующие (кнопка Удалить). Закладки идентичны шагу 2 и шагу 3 Мастера диаграмм. Для того чтобы добавить к построенной ранее диаграмме ещё
одну кривую нужно создать новый ряд по оси у. В OpenCalc при щелчке левой кнопкой мыши на область диаграммы появляется меню, где нужно выбрать пункт
Вставить/удалить оси, при нажатии на который всплывает окно (рис. 5) и добавляется ось.
Рис. 5.
Электронные таблицы хорошо справляются с задачей построения графика функции, заданной параметрически. В этом случае график определяется двумя функциями, явно выражающими обе координаты x=x(t) и y=y(t) через значение некоторого производящего параметра t.
Параметрические линии по форме более разнообразны, чем линии, описываемые одним уравнением. На них не распространяется ограничение по многозначности, поэтому линии могут быть самопересекающимися.
Excel предоставляет гораздо больший выбор видов диаграмм, чем Calc и Gnumeric, но, тем не менее, для отображения инженерных и экономических данных достаточно возможностей всех рассматриваемых табличных процессоров.
Многие инженерные, экономические задачи сводятся к таким матричным операциям, как умножение, сложение, вычитание, обращение, транспонирование матриц; вычисление определителя матрицы; решение систем линейных алгебраических уравнений. Подобные задачи хорошо решаются в табличных процессорах. Для выполнения операций над матрицами существуют
функции вычисления определителя и обратной матрицы, умножения матриц, формирования единичной матрицы. С помощью операций + и - реализуется сложение и вычитание матриц. Следует отметить, что работа с матрицами наиболее удобно осуществляется в OpenCalc [1].
Электронные таблицы позволяют решать нелинейные уравнения [2,3]. Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. Это основной способ решения нелинейных уравнений [2].
Кроме этого электронные таблицы позволяют решить нелинейное уравнение любым итерационным методом. В этом случае изменяется значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата. В качестве примера рассмотрим реализацию метода простой итерации в Excel [5].
Решить уравнение 2x – 1 = sinx методом простых итераций, с точностью е
=0,00001. Для выполнения итераций перепишем заданное уравнение так, чтобы в его левой части осталась только неизвестная переменная: x = (sinx + 1 ) /2
Построив график, можно определить, что интервал локализации корня – [0;2]. Рассматриваемое уравнение имеет единственный корень. В качестве начального приближения можно взять любое число, принадлежащее этому интервалу. Примем его равным 2.
Активизируем режим итераций. Выполним команду меню Сервис – Параметры. В диалоговом окне Параметры перейдем на вкладку Вычисления и установим флажок Итерации. Активизируем ручной режим вычислений, установив переключатель Вручную. Установим Предельное число итераций равное 1.
Значение Относительная погрешность оставим равным 0,001. Для этого достаточно четырех ячеек:
1) В ячейки А1, B1, C1, D1 вводим соответственно символы i, x, z, | z –x | – названия столбцов.
2) В ячейку A2 вводим число 1, равное порядковому номеру итерации.
3) В ячейку B2 вводим число 2, равное грубому начальному приближению корня, т.е. x1 = 2.
4) В ячейку C2 введем правую часть формулы метода простой итерации как выражение от B2=(sin(B2)+1)/2. Тем самым осуществлена первая итерация. Отметим, что вследствие установленного способа вычислений в Excel, ячейка с исходным значением должна находиться левее или выше ячейки с формулой.
5) В ячейку D2 введем формулу погрешности =ABS(C2–B2), нажимая клавишу
<Enter > при каждом вводе. Решение найдено. Корнем заданного уравнения является х= 0,88786.
Заданная точность решения е = 0,00001 обеспечена. Для решения потребовалось i = 10 итераций. Результат решения представлен в табл. 1.
Таблица 1
A |
B |
C |
D |
|
1 |
i |
x |
z |
| z – x | |
2 |
10 |
0,887868 |
0,887864 |
0.000004 |
Эту процедуру следовало бы повторить для других корней. Однако в нашем случае заданное уравнение имеет один единственный корень.
Системы нелинейных уравнений в электронных таблицах решаются путем сведения их к оптимизационной задаче. В состав всех рассматриваемых табличных процессоров входит оптимизационный модуль, однако только в MS Excel можно решать задачи нелинейной оптимизации. Для решения нелинейных задач оптимизации в OpenCalc можно использовать очень удачное расширение (с русским интерфейсом) японского программиста Kohei Yoshida Solver for Nonlinear Programming.
Наличие блока решения нелинейных оптимизационных задач в табличных процессорах позволяет решать ряд математических задач, таких, как системы нелинейных уравнений, задачи обработки экспериментальных данных.
Microsoft Office Excel, OpenOffice.org Calc и Gnumeric содержат большое количество статистических и финансовых функций.
Итак, очевидно, что исследуемые электронные таблицы имеют практически одинаковые возможности для решения инженерных и математических задач, за исключением некоторых нюансов. Однако, наличие нелинейного модуля оптимизации в MS Excel и OpenCalc позволяет решать многие сложные математические задачи (системы нелинейных уравнений, обработка экспериментальных данных методом наименьших квадратов и др.), которые ранее можно было решать только в специализированных математических пакетах. Следует отметить, что в MS Excel и OpenCalc входит мощный визуальный язык программирования, который позволяет запрограммировать решение любой математической задачи нереализованной встроенными функциями табличных процессоров. Открытость архитектуры OpenCalc позволяет добавлять внешние модули для решения различных задач.
Литература:
- Алексеев Е.Р. Использование свободных программ в научных исследованиях // Научно-практический журнал "Прикладная информатика" №6 (24) 2009. с. 61-79.
- Гельман В. Я. Решение математических задач средствами Excel: Практикум. – СПб, Питер, 2003.
- Орвис Вильям. Excel для ученых, инженеров и студентов. - Киев, Юниор, 1999.
- Козодаев Р., Маджугин А. OpenOffice.org 3. Полное руководство пользователя. — СПб БХВ-Петербург, 2009.
- Рональд У. Ларсен., Инженерные расчеты в Excel. – Москва, Вильямс,
2002.