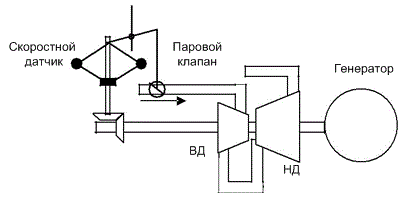
Рис. 4.1 Механическое ощущение скорости
Автор перевода: Л.Г. Черная
4.1 Исторический обзор измерения частоты
Измерение частоты энергосистемы использовалось начиная с появления генераторов переменного тока и систем. Скорость вращения роторов генератора непосредственно связана с частотой напряжений, которые они производят. (Рисунок 4.1) по существу измерительный прибор частоты, который используется в системе управления с обратной связью, чтобы держать машинную скорость в пределах ограниченного диапазона вокруг номинальной стоимости. Однако это измерение доступно только в электростанциях, и есть потребность в измерении частоты энергосистемы в сетевых шинах далеко от электростанций.

Рис. 4.1 Механическое ощущение скорости

Самое раннее измерение частоты было выполнено механическими устройствами, которые использовали механические резонаторы, настроенные на диапазон частот вокруг номинальной частоты (1). Такой частотомер показывают в рисунке 4.2 a. Другой измерительный прибор частоты приблизительно того же самого периода – устройство типа резонанса, посредством чего настроенные резонансные схемы в различных частотах возбуждены вторичным напряжением, полученным из трансформатора напряжения, и схема, которая находится в резонансе, обеспечивает измерение частоты (рисунок 4.2b) (1).
Рис. 4.2 (a) механический частотомер типа резонанса. (b) электрический частотомер типа резонанса. Эти инструменты для энергосистемы на 50 Гц.
Следующий прогресс в измерении частоты шел с введением точных техник измерений времени. Измеряя временной интервал между последовательными нулевыми перекрестками формы волны напряжения частота напряжения могла быть определена. Ясно точность такого измерения зависит от точности измерения времени, а также на точности, с которой могло быть определено нулевое пересечение формы волны. Это последнее измерение затронуто присутствием шума в измерении, переменных гармонических частотах и уровнях и исполнении пересекающих ноль схем датчика.
Синхронизированные фазные измерения дают возможность для измерения частоты энергосистемы, которая устраняет многие из этих ошибочных источников. Нужно отметить, что измерение частоты на энергосистеме прежде всего посвящено оценке скорости(ей) ротора подключенных генераторов. Также, измерение напряжения положительной последовательности – идеальная машина для измерения частоты. Кроме того, фазоры отражают фундаментальные компоненты частоты напряжений, и гармоники не влияют на измерение частоты, основанное на фазорах. Методы для измерения частоты фазорами описаны в следующих разделах.
4.2 Частота оценивается от трехфазового сбалансированного входного сигнала
Частота и уровень изменения частоты могут быть оценены от углов фаз (2). Было указано в Главе 3 что положительная последовательность оцененный от сбалансированных входящих сигналов имеет незначительное ослабление в фазной величине и как величина, так и фазные углым лишены ряби вторых гармоник. Приняв X2 = 0 в Eq. (3.22) получаем положительную последовательность напряжения

Величина P – фактор ослабления, и угол фазы P – постоянное погашение в измеренных углах фазы. Угол Xr1 сдвигается каждый раз. Предположим, что частоты положительной последовательности оценены за один период номинальной частоты, и что частоты вычислены по промежутку 3–6 циклов.
Если отклонение частоты от номинальной в любой момент времени “t”
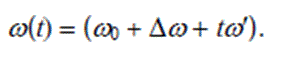

Угол фазы – интеграл частоты:
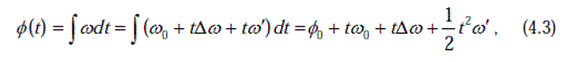
0 будучи начальным значением угла. Таким образом, угол фазы как функция времени
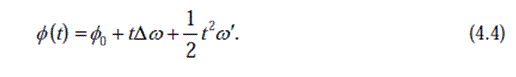
Предположим, что это полином времени второго порядка
следовательно в момент времени t=0

или
Ниже представлен вектор измерений
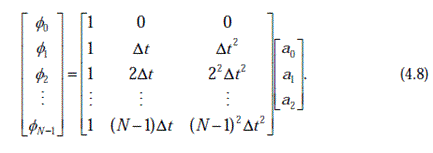
В матричном виде
где (B) – содействующая матрица в Eq. (4.8). Неизвестный вектор
вычисленный методом метода взвешенных наименьших квадратов (ВНК):
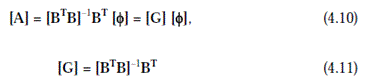
Матрица (G) предварительно вычислена и сохранена для использования в режиме реального времени. Она имеет
“N” рядов и три колонки. В режиме реального времени (G) умножен на (B), чтобы получить
вектор (А).
4.3 Частота оценивает от неуравновешенных входов
Эффект отсутствия равновесия во входных сигналах был проанализирован в Разделе 3.5. Уравнение (3.22) обеспечивает формулу для оценки положительной последовательности, когда есть компонент отрицательной последовательности во входном сигнале:

где Q дана Eq. (3.11), и X2 компонент отрицательной последовательности во входных сигналах. Эти волны могут быть устранены одним из описанных методов фильтрации в Разделе 3.3. Когда волны устранены, частота и уровень изменения частоты может быть оценен как в Разделе 4.2.
4.4 Нелинейные оценивания частоты
Возможно сформулировать проблему оценки частоты и уровня изменения частоты как проблему нелинейной оценки входного сигнала (3, 4). Рассмотрим вход единственной фазы(как в Eq. 4.4):
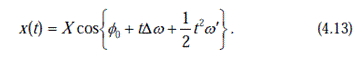
Предполагается, что есть четыре неизвестных

Функция x (t) является нелинейной функцией этих четырех неизвестных, и если “N” больше, чем четыре, нелинейный метод взвешенных наименьших квадратов повторяющаяся техника может использоваться, чтобы решить для этих четырех неизвестных.
Принимая разумные начальные значения этих четырех неизвестных как (z0), начальная буква оценки функции x (t) (x0). Использование терминов первого порядка Тейлора ряд, чтобы представлять нелинейную функцию вокруг (z0).

Представление матрицы частичных производных якобиевской матрицей (J), решением для метода взвешенных наименьших квадратов поскольку (z)
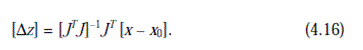
Четыре производных находятся из уравнений
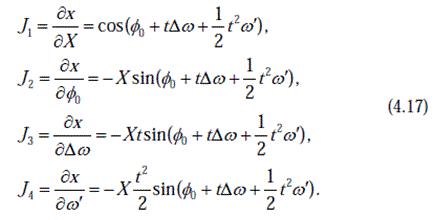
Вычислив исправления (z) в Eq. (4.16), они добавлены к (z0)
для получения ответа в конце первого повторения. Процесс повторяется, пока остаток (x – x0) не становится меньшим, чем подходящая устойчивость.
Пример 4.2 Числовой пример нелинейной частоты и уровень оценки изменения частоты.
Рассмотрим однофазный входной сигнал с амплитудой 1.1, частота 60.5 Hz в t = 0, уровень изменения частоты 1 Hz s–1 и фаза поворачивается 0 из /8. Начальные значения для старта повторения, как предполагается,
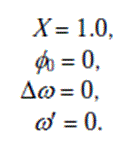
Таблица 4.3 показывает первые 10 величин входного сигнала

Вектор корректировок выглядит следующим образом
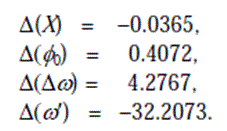
После четырех итераций правильные величины неизвестных были получены
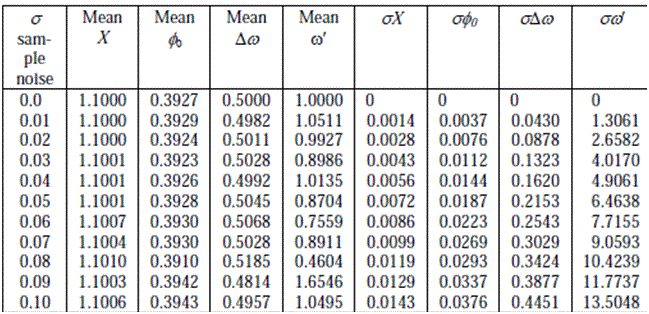
Необходимо рассмотреть эффект шума. Этот критерий был добавлен после получения результатов испытаний, которые показаны в таблице 4.4.
Уровень изменения частоты
практически непригодно, когда шум превышает 1% амплитудного значения сигнала. Амплитуда и угловые оценки фазы довольно хороши даже для ошибок очень большой выборки.
4.5 Другие Методы для измерений частоты
Много других методов для измерения частоты энергосистемы описаны в технической литературе (5, 6, 7, 8). Эти ссылки предусмотренный, заинтересованный читатель, как образец того, что доступно, и ни в коем случае полный список бумаг, имеющих дело с измерением частоты. В целом, более быстрые подходы (измерения сделаны в пределах одного
или двух периодов), имеют тенденцию иметь большие ошибки чем те, которые используют более длинные окна данных. Не нужно брать чрезмерно много данных для оценки частоты
чтобы улучшить точность оценки. Во время переходного процесса колебание стабильности, частота энергосистемы может измениться быстро. Таким образом длинное окно может включать существенно отличающиеся частоты и приводить к ошибке. Мы рассмотрим эффект изменяющейся частоты из–за переходных процессов в Главе 6.
Литература: