Аннотация
Е. Нолле, Н. Нойбергер Наблюдатель теплового состояния асинхронного электропривода в контексте стратегии максимального использования его перегрузочной способности Рассмотрена проблема косвенного определения температуры и обеспечения максимальной производительности механизмов повторно-кратковременного режима работы с неопределенным рабочим циклом. Представлена методика определения температуры асинхронного двигателя с помощью трехмассовой динамической тепловой модели. В методике учтена нестационарность составляющих потерь и теплоотдачи двигателя при регулировании скорости и нагрузки. Получены зависимости и предложен подход к регулированию асинхронным электроприводом, что позволяет сформировать такой рабочий цикл, при котором двигатель будет максимально использован по перегрузочной способности.
АКТУАЛЬНІСТЬ РОБОТИ
Широке впровадження асинхронного частотно-регульованого електропривода обумовило необхідність переглянути деякі підходи, пов’язані з навантажувальною здатністю електромеханічної системи. Мова йде про методи вибору й перевірки двигуна, такі, як методи еквівалентного струму та моменту, а також налагодження систем захисту від теплового перевантаження. Традиційно вибір і перевірка електродвигуна та його захист у процесі експлуатації здійснюється за наступними припущеннями [1]:
- двигун розглядається як одномасове однорідне тіло, тобто використовується одномасова теплова модель;
- тепловіддача вважається сталою;
- основні втрати розділяють на постійні (втрати в сталі, механічні) та змінні – ті, що залежать від навантаження (електричні втрати в обмотках статора і ротора).
Недосконалість одномасової теплової моделі для уточнених розрахунків добре доведена [2, 3]. При її використанні є небезпека «пропустити» перевищення температури критичного вузла асинхронного двигуна (АД) – ізоляції статора, яка, внаслідок теплової інерційності й фактичної неоднорідності, може на 10–20 °С перевищувати температуру корпуса [4].
Щодо врахування зміни інтенсивності тепловіддачі зазвичай використовуються спеціальні коефіцієнти [1], які враховують погіршення умов охолодження при загальмованому роторі електродвигуна. В механізмах з незначною долею перехідних режимів у робочому циклі таке припущення дійсно коректне. Але у випадку, коли двигун тривало експлуатується із швидкістю, відмінною від номінальної, таким методом користуватись не можна.
Також слід враховувати те, що структура втрат в АД при використанні частотного регулювання суттєво відрізняється від відповідного їх розподілу при безпосередньому живленні від мережі. Це стосується, в першу чергу, втрат у сталі. Для електродвигунів з номінальною напругою 0,4 кВ ці втрати складають приблизно половину загальних втрат, що гріють. Для регулювання швидкості перетворювач змінює величину напруги й частоти на вході АД, змінюючи, таким чином, й інтенсивність магнітного поля.
Отже, інтенсивність охолодження, результуючі втрати в асинхронному двигуні є складною функцією навантаження та швидкості обертання. Коригування підходів до вибору й перевірки двигуна за нагріванням, а також організації захисту двигунів особливо актуальне для механізмів повторно-короткочасного режиму роботи.
При проектуванні та модернізації електропривода виникає також невизначеність у виборі перетворювача частоти. Виробники перетворювачів нормують номінальний струм перетворювача та його перевантажувальну здатність. Це, зазвичай, 150 % номінального струму впродовж однієї хвилини. Між тим незрозуміло, як перевантажувальна здатність і тривалість такого перевантаження може бути однаковою для перетворювачів зовсім різних типорозмірів. Некоректний вибір перетворювача, причому в обох варіантах – як заниженої, так і завищеної потужності, означає втрати в будь-якому випадку. Це або непрацездатність системи при недостачі навантажувальної здатності, або завищені витрати і, таким чином, висока ймовірність програшу в конкурентній боротьбі у випадку встановлення «завеликого» перетворювача.
Також незрозуміло, чи слід навантаження двигуна приводити до тривалості включення ТВ=100 %? Чи не встигне перетворювач вийти на сталу температуру під час робочої частини циклу? Ці питання особливо актуальні для асинхронних електроприводів малої потужності, в яких, як буде показано далі, теплові сталі часу перетворювача й електродвигуна мають один порядок.
Для коректної відповіді на ці питання, на наш погляд, слід використовувати спостерігач теплового стану всієї електромеханічної системи – асинхронного двигуна й перетворювача частоти. Структура теплової моделі з урахуванням перетворювача частоти показана на рис. 1.
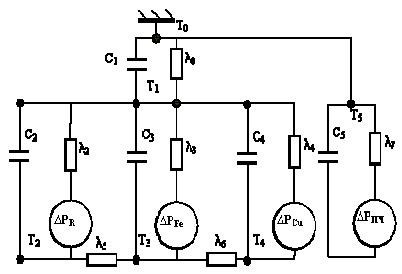
Рисунок 1 - Динамічна теплова модель системи ПЧ–АД
Асинхронний двигун представлений тримасовою моделлю, кожній масі в якої відповідає три джерела втрат, що гріють:
- електричні втрати в обмотці статора (відповідно, у вузлі розраховується температура обмотки статора);
- втрати в сталі (у вузлі розраховується температура осердя);
- електричні втрати в обмотці ротора (температура ротора).
Перетворювач частоти представлений одномасовою тепловою моделлю з параметрами α7, C7, ΔPfc
При регулюванні швидкості асинхронного двигуна частотний перетворювач змінює параметри живлення, змінюючи, таким чином, інтенсивність магнітного поля й відповідні втрати. Прийнято, що втрати в сталі залежать від напруги та частоти наступним чином [6]:

де Unom, fnom – відповідно номінальна напруга й частота живлення АД; kU, kf – коефіцієнти, що залежать від параметрів сталі та конструкції.
Електричні втрати розраховуються за відомими формулами [1]. Наприклад, для традиційного закону скалярного керування U/f = const результуючі втрати при регулюванні швидкості будуть змінюватись так, як показано на рис. 2.
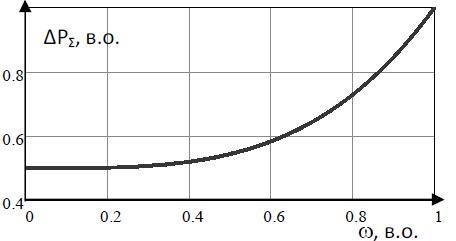
Рисунок 2 – Залежність результуючих втрат у функції швидкості обертання двигуна
Щодо джерела втрат у перетворювачі частоти, вони залежать від струму ПЧ та частоти комутації.
На відміну від одномасової моделі, яка характеризується однією тепловою ємністю, кожному вузлу відповідає своя ємність С1, С2 і С3, яка характеризує інерційність процесів теплопередачі.
Тепловіддача у навколишнє середовище представлена тепловою провідністю λ1(ω) , яка є функцією швидкості обертання двигуна. Вважається [7], що, наприклад, для двигунів захищеного виконання ця залежність квадратична й має вигляд, представлений на рис. 3.

Рисунок 3 – Залежність тепловіддачі у функції швидкості обертання двигуна
Отже, при зниженні швидкості обертання відбуваються дві речі: знижуються сумарні гріючі втрати, що є добре, та, водночас, погіршуються умови охолодження. Звісно, у більшості випадків швидкість механізму та його навантаження диктуються технологією і тому ці співвідношення не можуть бути використані для оптимізації роботи електропривода. Але наведене показує, що при зниженні швидкості АД навантажувальна здатність змінюється неоднозначним чином.
Визначимо залежність максимальної температури, яку досягають конструктивні вузли асинхронного двигуна під час роботи в повторно-короткочасному квазіусталеному режимі. Визначимо також динаміку нагріву перетворювача частоти.
Для вирішення поставленої задачі скористаємось рівняннями, які описують динамічну теплову модель. Кожне рівняння записується для окремого вузла, воно, фактично, відбиває рівняння теплового балансу:

де Τi – абсолютна температура i-го вузла; Ci, Αi – відповідно теплова ємність і провідність; ΔPi – гріючі втрати в і-му вузлі.
Звернемо увагу, що рівняння теплової моделі можуть бути записані як для значень перевищення температури кожного вузла над температурою навколишнього середовища, так і для абсолютних температур, оскільки інтенсивність теплового потоку і відповідні рівняння визначаються різницею температур окремих вузлів. В останньому випадку в моделі фігурує значення температури навколишнього середовища τ0. Для зручності запису для позначення температури збережений символ τ.
Таким чином, повна система рівнянь, що описує представлену теплову модель, матиме вигляд:
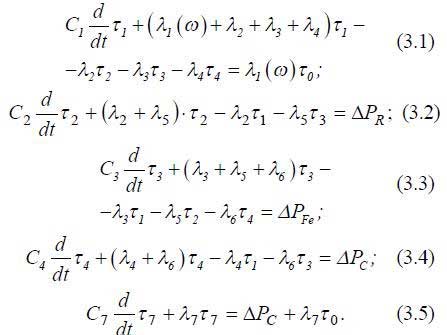
Наведені рівняння записано відповідно до корпусу (τ1), обмотки ротора (τ2), осердя (τ3), обмотки статора (τ4) та температури радіатора перетворювача частоти (τ7). У матричному вигляді представлена система рівнянь матиме вигляд:
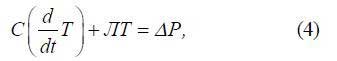
де С – діагональна матриця теплових ємностей (5x5); Т – матриця відповідних температур (5x1),
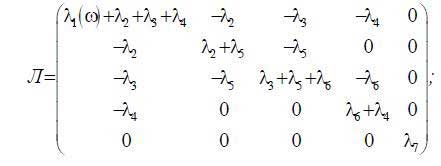
ΔP – матриця втрат і тепловіддачі, яка відбиває праву частину системи рівнянь (3), розміром (5x1).
Для отримання аналітичної залежності між максимальною температурою і параметрами циклу розглянемо спрощений робочий цикл, зображений на рис. 4.
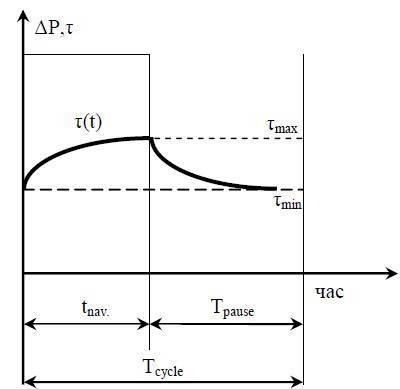
Рисунок 4 – Спрощений цикл навантаження механізму повторно-короткочасного режиму роботи
У зображеному циклі знехтувано зміною втрат і тепловіддачі в перехідних режимах, розглядається тільки два стани системи – навантаження/пауза.
Вирішення матричного диференційного рівняння (4) для режиму навантаження має вигляд:

У рівнянні (5) Тust – матриця усталених температур при роботі з певним навантаженням, визначається як

У рівнянні (5) фігурує матриця Лnav., яка відповідає матриці теплових провідностей для режиму обертання електродвигуна.
Тmin – матриця початкових значень температур, у квазіусталеному режимі ці значення дорівнюють величинам температур, які досягаються після охолодження за час паузи:

У рівнянні (7) матриця Лpause відповідає матриці теплових провідностей для загальмованого двигуна, матриця Т0 – матриця-стовбець із температурами τ0.
Сумісне вирішення рівнянь (6) і (7) дає вираз
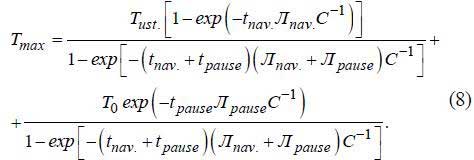
Матричне рівняння (8) є залежністю температур вузлів електромеханічної системи від параметрів робочого циклу: тривалості навантаження і пауз, величини навантаження (воно опосередковано визначає матрицю усталеної температури Тust.) та величини швидкості в режимах навантаження і паузи, яка визначає тепловіддачу в навколишнє середовище і таким чином матрицю Л.
За допомогою цього рівняння можна визначити такі параметри циклу, за якими не трапляється перевищення допустимої температури ізоляції статора.
Існує певний клас промислових механізмів з невизначеним робочім циклом, до якого можна віднести технологічні крани, наприклад, портові грейферні, і такі механізми, як шліфувальні верстати. Такі механізми обладнані, зазвичай, регульованими приводами середньої потужності (10 –100 кВт). Зазвичай тривалість роботи цих механізмів порівняно із сталою нагріву двигунів. Таким чином, існує можливість завдання таких параметрів робочого циклу, за яких приводні двигуни максимально використовуються за потужністю, забезпечуючи максимально можливу продуктивність. Для цього можна змінити обмеження швидкості не «головного» приводу, який зазвичай визначає продуктивність механізму (привод головного підйому, обертання шпинделя), а допоміжних – приводів повороту стріли крану або приводу подачі.
Для перевірки залежності (8) було проведене моделювання спрощеного робочого циклу. Для моделювання були використані дані про теплові ємності та провідності АД і перетворювача частоти, отримані експериментальним шляхом в умовах лабораторії електромеханіки Есслінгенського університету прикладних наук (ФРН) [4].
.Дані наведено в табл. 1.
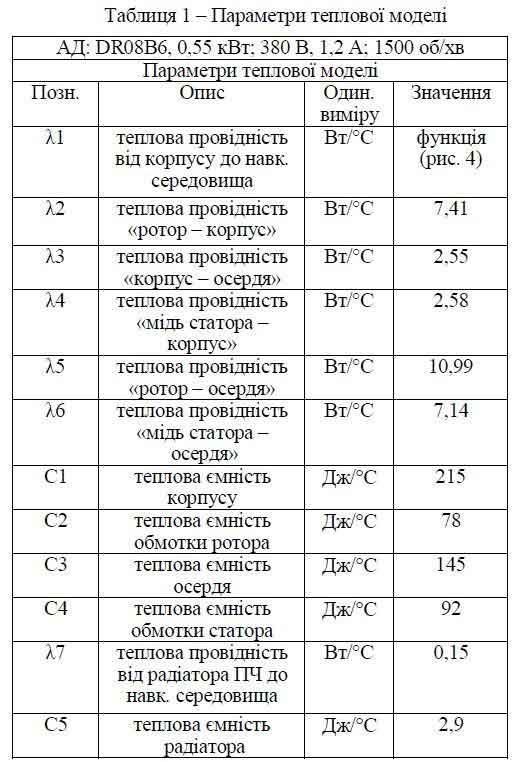
На рис. 5 показано фрагмент діаграми навантаження механізму в квазіусталеному режимі.

Рисунок 5 – Температури конструктивних частин АД і радіатора ПЧ у спрощеному циклі навантаження: 1 – перетворювача; 2 – сталі; 3 – корпусу; 4 – ротору; 5 – статору
Моделювання свідчить, що теплова інерційність грає значну роль у процесах нагріву/охолодження двигуна. Із початком ділянки навантаження інтенсивність зниження температури корпусу навіть посилюється – це пов’язано з тим, що при обертанні двигуна суттєво збільшилась тепловіддача й водночас потік тепла від джерел «запізнюється». У режимі паузи спостерігається зворотна картина.
Для наведених параметрів моделювання температури осердя та обмотки статора наприкінці ділянки навантаження фактично збігаються.
У наданому випадку температура радіатора перетворювача має також квазіусталений характер. Між тим дослідження класу інших електромеханічних систем показало, що це притаманно тільки електроприводам дуже малої потужності (до 1 кВт).
Зазвичай під час навантаження температура радіатора ПЧ досягає свого усталеного значення. Таким чином, під час вибору ПЧ для механізму режиму S3 не слід приводити навантаження електродвигуна до ТВ=100 %. ПЧ слід обирати за струмом АД для ділянки навантаження, тобто значення, вказаного на шильдику.
ВИСНОВКИ
У випадку регульованого асинхронного електропривода для механізмів повторно-короткочасного режиму роботи, для вибору електродвигуна та перетворювача неприпустиме використання формул еквівалентного струму та моменту.
Температурний режим асинхронного двигуна може бути прогнозований за допомогою тримасової динамічної теплової моделі з урахуванням залежності тепловіддачі від швидкості обертання, а також зміни складових втрат при регулюванні швидкості.
Максимальне використання асинхронного електропривода за навантажувальною здатністю може бути забезпечено шляхом зміни параметрів робочого циклу таким чином, щоб співвідношення складових втрат та тепловіддачі двигуна обумовило неперевищення допустимої температури ізоляції статора.
Під час вибору перетворювачів частоти для двигунів потужністю більше 1 кВт не слід приводити навантаження електродвигуна до тривалого режиму роботи, оскільки стала нагріву перетворювача обумовлює досягнення усталеної температури радіатора під час навантаження.
ЛІТЕРАТУРА
1. Колб А.А., Колб А.А. Теорія електроприводу: навчальний посібник. – Донецьк: Національний гірничий університет, 2006. – 511 с.
2. Бешта А.С., Худолей С.С., Neuberger N., Nolle E. Диагностика теплового состояния асинхронного двигателя // Сб. науч. тр. Днепродзержинского государственного технического университета (технические науки). Тематический выпуск «Проблемы автоматизированного электропривода. Теория и практика». – Днепродзержинск: ДГТУ, 2007. – С. 469–472.
3. Бешта О.С., Худолій С.С., Neuberger N, Nolle E. Спостерігач теплового стану асинхронного електродвигуна // Тематичний випуск «Проблеми автоматизованого електропривода. Теорія й практика» науковотехнічного журналу «ЕЛЕКТРОІНФОРМ». – Львів: ЕКРінформ, 2009. – С. 258–260.
4. S. Khudoliy, N. Neuberger, E. Nolle. Rotorerwarmung bei Umrichter gespeisten Asynchronmaschinen. Spektrum-Zeitschrift der HS-Esslingen, 26/2007.
5. Vacon NXP/C User's Manual. – Режим доступу: http://www.vacon.com.
6. Бешта О.С. Ідентифікація параметрів електропривода в задачах енерго- і ресурсозбереження (розвиток теорії, розробка і впровадження: автореф. Дис. на
здоб. наук. ступеня д-ра техн. наук: спец. 05.09.03. – Дніпропетровськ, 2001. – 38 с.
7. Fundamentals of a Motor Thermal Model and its Applications in Motor Protection B. Venkataraman, B. Godsey Black & Veatch Corporation W. Premerlani
GE Global Research Niskayuna, New York / E. Shulman, M. Thakur, R. Midence, GE Multilin Markham, Ontario.