Аннотация
Милых В.И., Майстренко А.М. ВИРТУАЛЬНЫЙ СТЕНД ДЛЯ ИССЛЕДОВАНИЯ ДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА
Введение.
За последнее десятилетие технологии компьютерного моделирования настолько крепко зарекомендовали себя во всех областях науки и техники, что сегодня уже сложно представить себе инженерную науку без компьютерного моделирования и визуализации. Виртуальная реальность [1] – детище информационной эры постепенно становится стандартом инженерного образования [2]. Для этого есть множество причин, главные из которых – неразрешимые проблемы организации полноценных реальных практикумов, интенсивное внедрение высоких технологий в производственную сферу жизнедеятельности [3].
Общая концепция работы.
В отмеченных условиях сформулирован и поэтапно осуществляется проект, общей целью которого является разработка единой концепции создания виртуальных лабораторных стендов. В перспективе открывается возможность перехода на производственный уровень подготовки целых виртуальных учебных лабораторий. Такой подход позволит повысить качество образования за счёт массового включения в учебные курсы лабораторных практикумов, содержащих любые технические устройства, для которых возможно формулирование математических моделей.
Цель работы
Cоздание виртуального стенда для исследования двигателя постоянного тока (ДПТ), что является одним из этапов достижения общей цели. В соответствии с этим на основе классических уравнений для ДПТ [4] разработана спе-циализированная математическая модель, которая позволяет объединить графическую трехмерную модель виртуального стенда и окружающего её пространства лаборатории с эмуляционной математической моделью. Такое объединение есть не что иное, как виртуальная реальность.
Материалы и результаты исследований
Математическая модель виртуального стенда, его описание и функциональные возможности. Виртуальный лабораторный стенд внешне представляет собой фотореалистичную графическую модель

Рисунок 1 - Общий вид лабораторного стенда
Принципиальная электромеханическая схема исследуемой системы дана на рис. 2. Здесь рассматривается вариант ДПТ с независимым воз-буждением. Его номинальные параметры считаются заданными.
Математическая модель данного ДПТ соответствует классическим представлениям о нем [4], но с некоторыми уточнениями, сохраняющими реалистичные для ДПТ нелинейности магнитных характеристик.
Прежде всего, задается реальная магнитная ха-рактеристика возбуждения - зависимость полезного магнитного потока, создаваемого обмоткой возбуждения и входящего в якорь в режиме холостого хода, от тока обмотки возбуждения (рис. 3, а). При постановке математической модели для можно использовать подходящую аппроксимирующую функцию, в простейшем случае - кубический полином 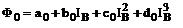 в который входят определенные коэффициенты. Также учитывается влияние реакции якоря, как показано на рис. 3, б, где полезный поток в якоре зависит от тока якоря . На отладочном этапе принимается семейство линейных зависимостей (на рис. 3, б даны две из них):
в который входят определенные коэффициенты. Также учитывается влияние реакции якоря, как показано на рис. 3, б, где полезный поток в якоре зависит от тока якоря . На отладочном этапе принимается семейство линейных зависимостей (на рис. 3, б даны две из них):
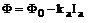 (1)
(1)

Рисунок 2 - Принципиальная электромеханическая схема для исследования ДПТ
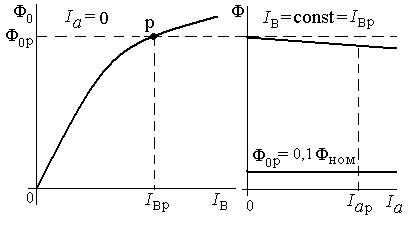
Рисунок 3 - Магнитные характеристики ДПТ
Где коэффициент является функцией потока
является функцией потока 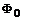 и уменьшается до нуля, например, при
и уменьшается до нуля, например, при (
(  - номинальный поток).
- номинальный поток).
Линеаризованный в первом приближении коэф-фициент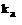 в дальнейшем может быть заменен более точным - нелинейным коэффициентом.
в дальнейшем может быть заменен более точным - нелинейным коэффициентом.
Итак, первым шагом будем считать выставление некоторого (регулируемого) тока возбуждения ДПТ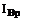 что дает конкретные значения потока возбуждения
что дает конкретные значения потока возбуждения  (рис. 3, а), а, следовательно, и коэффициента
(рис. 3, а), а, следовательно, и коэффициента 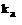 (рис. 3, а), а, следовательно, и коэффициента . Также выставляются определенные значения напряжения питания U и сопротивления регулировочного реостата
(рис. 3, а), а, следовательно, и коэффициента . Также выставляются определенные значения напряжения питания U и сопротивления регулировочного реостата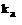 в якорной цепи.
в якорной цепи.
Передвижение по лаборатории, коммутация це-пей, регулирование напряжения и параметров на-грузки, пределов измерения осуществляются по-средством стрелочных клавиш клавиатуры и мыши.
Посредством изменения тока в обмотке электромагнитного тормоза (ОЭМТ) создается эффект задания механической нагрузки двигателя (рис. 4). Однако отправной величиной удобно принять не момент вращения на валу, а электромагнитный момент якоря . Тогда из известного выражения последнего [4] с учетом (1) получается:
 (2)
(2)
Откуда определяется ток якоря как решение квадратного уравнения (
как решение квадратного уравнения (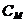 - известный конструктивный коэффициент ДПТ).
- известный конструктивный коэффициент ДПТ).
Теперь можно использовать уравнение напряжений якорной цепи ДПТ:
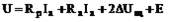 (3)
(3)

Рисунок 4 - Электромагнитный тормоз, измеритель момента и мультиметр
Где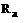 сопротивление якорной цепи, включая обмотки якоря и дополнительных полюсов;
сопротивление якорной цепи, включая обмотки якоря и дополнительных полюсов;  - падение напряжения в щеточно-коллекторном контакте (принимается постоянным).
- падение напряжения в щеточно-коллекторном контакте (принимается постоянным).
Очевидно, что из (3) определяется ЭДС обмотки якоря Е. С учетом известного ее выражения [4] и (1):
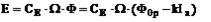 (4)
(4)
находится угловая скорость вращения якоря:
 (5)
(5)
Где тот же, что и
тот же, что и 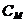 в (2), конструктивный коэффициент ДПТ.
в (2), конструктивный коэффициент ДПТ.
Путь к моменту вращения на валу проходит че-рез определение полезной мощности ДПТ:
 (6)
(6)
Где  электромагнитная мощность;
электромагнитная мощность;  - механические потери (по опыту [5] - функция
- механические потери (по опыту [5] - функция  с определенными коэффициентами
с определенными коэффициентами );
); 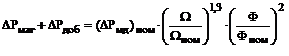 - магнитные и добавочные потери, пересчитываемые от их суммы
- магнитные и добавочные потери, пересчитываемые от их суммы 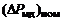 при номинальных угловой скорости
при номинальных угловой скорости  и потоке
и потоке
В итоге момент вращения на валу:
 (7)
(7)
В результате расчёта по алгоритму, построенному на основе математической модели, на приборы виртуального стенда (рис. 5) могут быть выданы значения следующих величин: ток якоря; M - момент на валу; n - частота вращения (считается через
ток якоря; M - момент на валу; n - частота вращения (считается через и измеряется посредством тахогенератора и тахометра);
и измеряется посредством тахогенератора и тахометра);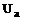 - напряжение на входных зажимах якорной цепи ДПТ
- напряжение на входных зажимах якорной цепи ДПТ 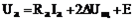 .
.
Кроме этого есть несколько приборов, которые регистрируют изменяемые самим пользователем значения: U - напряжение питания; - ток возбуждения, ток в ОЭМТ и т.д.
- ток возбуждения, ток в ОЭМТ и т.д.

Рисунок 5 - Приборная панель и стол с выключате-лями и регулировочными реостатами
Используя «экспериментальные» значения величин, «измеренные» на виртуальном стенде, можно дополнительно определить: мощность, потребляемую ДПТ из сети:  ; КПД:
; КПД: (без учета мощности на возбуждение или с нею при
(без учета мощности на возбуждение или с нею при  .
.
Все виртуальные действия, измерения и вычис-ления дают возможность построить рабочие характеристики ДПТ: ;
;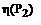 ;
;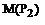 ;
;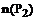 .
.
Варьированием величин 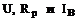 при заданном моменте вращения на валу можно изучить регулировочные свойства ДПТ и построить различные его регулировочные характеристики.
при заданном моменте вращения на валу можно изучить регулировочные свойства ДПТ и построить различные его регулировочные характеристики.
Графическая модель на этапе программирования снабжается набором т.н. триггеров и слайдеров – программно-логических элементов, которые внешне представлены элементами графической модели (ручка регулятора, стрелка прибора, текстура цифрового мультиметра и т.д.), а функционально играют роль регуляторов и переключателей.
Взаимообратная связь между математической и графической моделями осуществляется посредством коэффициентных функций слайдеров и триггеров. За счёт использования коэффициентных промежуточных функций достигается дифференциация графического и интерактивного модуля от математического модуля.
Используются специальные математические модели, не содержащие производных. Пересчёт математической модели проводится только тогда, когда изменяются значения в промежуточных функциях триггеров или слайдеров. Такой подход позволяет снизить процессорную загрузку. Это необходимо для синхронизации расчёта графической и математической моделей. Так как состояние графической модели для её приемлемого функционирования и отображения необходимо просчитывать десятки раз в секунду, т.е. значение fps (frames per second - кадров в секунду) должно быть не менее 60, и чем выше это значение, тем более «натурально» будет вы-глядеть все виртуальное пространство. Такие интенсивные вычисления требуют много процессорного времени, в то время как расчет математической модели также является ресурсоемким процессом.
Графическая модель создаётся в специальных пакетах трёхмерного моделирования (3D MAX [6], Maya, LightWave). Программирование вир-туального пространства, математической модели и сопутствующих сервисных программных модулей осуществляется в пакетах мультимедийного программирования (Adobe Director [7], Visual C.NET с использованием OpenGL или DirectX, VRML, Cult 3D).
Выводы.
Виртуальная реальность во многих случаях является эффективной альтернативой [1.C,1.E,1.F] другим формам представления учебной информации, требующей постановки эксперимен-тов, которые не могут быть выполнены в реальности по целому ряду причин. Разработка единой схемы производства виртуальных лабораторий позволит существенно снизить затраты на их разработку, позволит также значительно снизить требуемый про-фессиональный уровень программистов, занимаю-щихся производством виртуальных лабораторных работ. В Национальном техническом университете «ХПИ» проводится разработка виртуального прак-тикума для студентов электротехнических специ-альностей, который, в принципе, может быть рас-пространен и на студентов неэлектротехнических специальности. Для разработки виртуального электротехнического практикума используется опыт создания физического виртуального практикума, который уже несколько лет активно используется. Проводятся методико-педагогические эксперименты с целью выявления направлений развития, приводящих к повышению образовательного эффекта от использования виртуальных лабораторий, как альтернативы реальным аналогам. Намечены научные эксперименты по исследованию аппаратных средств виртуальной реальности и их интегрированию с виртуальными лабораториями.
Список использованной литературы
1. Burdea, G. and P. Coiffet. 1994. Virtual Reality Technology. John Wiley and Sons: New York, NY.
A. Durlach N. I. and A.S. Mavor (Eds). 1995. Vir-tual Reality Scientific and Technological Challenges. National Academy Press: Washington, DC.
B. Виртуальная реальность http://www.lotus.com/learningspace
C. Hoffman H., Vu D. Virtual reality: teaching tool of the twenty-first century. Academic Medicine. 1997;72:1076-1081
D. Haggerty T.R. Influence of information technologies on kinesiology and physical education. Quest 1997;49:254-269.
E. Brown D., Wilson J. LIVE: learning in virtual environments. Ability 1995;15:24-25.
F. Yoshikawa H., Tezuka T., Kashiwa K., Ishii H. Simulation of machine-maintenance training in virtual environment . Journal of the Atomic Energy Society of Japan 1997;39:1078-1089.
2. Программа заседания круглого стола "Ин-формационные средства обучения для повышения качества инженерного образования"http://CONFERENS.SUMDU.EDU.UA/DL2004/RU/PROGRAM/SEMINAR/2004_03_17/
3. Центр высокопроизводительных вычисли-тельных кластерных технологий .http://WWW.PARACOMTECH.RU/
4. Вольдек А.И. Электрические машины. Л.: Энергия, 1978.- 832 с.
5. Проектирование электрических машин: Учебное пособие для ВУЗов / И.П. Копылов, Ф.А. Горяинов, Б.К. Клоков и др.; Под ред. И.П. Копылова. М.: Энергия, 1980. -496 с., ил.
7.http://www.macromedia.com/software/director