Параметры режима при передачи мощности энергосистеме.
Оригинал: http://www.sei.irk.ru/aec/proc2004/39.pdf
Перевод: Цветов А.С.
Краткий обзор. Параметры режима позволяют оценить степень приближения к предельным режимам, эффективность существующего электрического режима. Вторые производные от системной функции могут быть обобщенными параметрами. Они характеризуют степень изменения процесса в данном направлении, применяемых для решения расчетных задач в режиме оптимизации.
Ключевые слова — реальный поток, коэффициент запаса, совокупные потери действительные мощности, функция, обобщённые параметры, вторые производные числа.
I. Введение
Основная задача управления нормальными электрическими режимами (НЭР) в электроэнергетической системе (ЭЭС), заключается в предоставлении потребителям электрической энергии требуемого качества при минимально возможных эксплуатационных затратах в системе. В договорных отношения между объектами энергетики существует необходимость компромиссного подхода к ее решению [1]. Автоматизированной система диспетчеризации (АСД) работает в нормальном и послеаварийном режимах необходима для оценки статической устойчивости, экономичности, надежности, а также для определения областей допустимых НЭР (AНЭР) и режимы управления (AЕР) электроэнергетическими системами. Максимальные границы для режимов АЭР, но АНЭР внутри AЭР на некотором расстоянии от границы (запасов). В общем случае задача поиска граничного режима сформулирована как поиск границы в AЭР на данном пути, в детерминант направлении его становления тяжелее [2] на физически проданных независимых переменных.
Одна из проблем при планировании работы электроэнергетических систем, является необходимость найти предел реальной пропускной способности, который может быть часто, определяться рядом вычислений для (последовательно отражается на любом параметре) режима. Увеличение диапазона проводится таким образом, что поток мощности в передающей сети (отдельная ЛЭП) изменяется сильнее [2]. Режим считают допустимым при проверке на статическую устойчивость, если полученные статические коэффициенты запаса устойчивости при мощности Kp или напряжение Ку не меньше, чем нормативные. Эксплуатационные стандарты предполагают коэффициенты запаса реальной мощности не меньше, чем 20% в нормальном и 8% — в послеаварийных режимах.
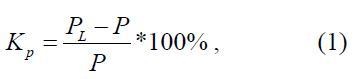
где Р – действительная мощность;
РL – пропускная способность линии (TL).
Коэффициент запаса по напряжению определяется следующим способом:
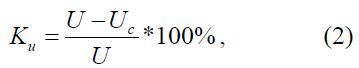
где Uc - критическое напряжение цепи, рассчитанное с характеристиками нагрузки или полученными 75% от напряжения в нормальном режиме. Значение Кu должно быть не менее 15% в нормальном и 10% - в послеаварийном режиме .Если серии расчетов проводились при различных видах увеличение нагрузки , можно определить коэффициент запаса устойчивости в этом случае [3]
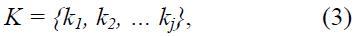
где j = 1... J-число режимов. В увеличении запаса режима только Р и коэфициент запаса U вычислены аналогично к Кj. Обычно норма коэффициента запаса может быть получена m-нормой:
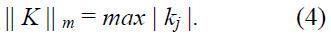
Данный коэффициент является необходимым и достаточным условием для оценки статической устойчивости системе в различных режимах роботы. Коэффициенты нормативного запаса, полученные обычным путем, являются постоянными величинами, отрегулированными отдельно для устойчивого нормального, и отправляют случайные эксплуатационные условия, которые не определяют степень "тяжелой" схемы и ситуации со способами в системе. Поэтому анализ обобщенных параметров режима, разрешающих получить коэффициенты запаса, связанные и с существующей ситуацией, и с методом увеличения веса режима.
II. Постановка задачи
На рынке электроэнергии существует острая необходимость в новых методах анализа электроэнергетических систем. Таким образом исследование устойчивости энергосистем необходимо для контроля по стабилизации режима. Автоматизированная система диспетчерское управление (АСДУ) электрических режимов традиционно решает проблемы, вызывающие к оптимальному управлению режимами. Контроль режимов электрической системы внедряет на основе решения задач расчета и оптимизации режимов оценка их стабильности. Разработка и оценка возможности использования параметров обобщенного режима позволяющий определить область допустимых режимов (ОДР). Граница такого ОДР должна отделять область нормальной работы системы от области, в которой один уровень стабильности, надежности и рентабельности режима быстро снижается.
III. Математическая модель
Желательно определить объединенный параметр запасов при межправительственном энергетическом обмене. Выбором объединенного параметра запаса его соответствие многим требованиям, таким как универсальность, доступность, способность получения на базисной информации о режимах, возможность характеризовать режим. Возможно обнаружить представительные особенности режимов, которые одновременно могут быть параметрами запасов, будучи функциями, правильно оценивающими степень приближения к пределу режима, разрешая оценивать уровень [4,5] надежности и доходность, существующую из электрических режимов. Тогда необходимо обнаружить обобщенные параметры режима, такие как:
- определить важность реальных запасов до границ ОДР, используя реальную способность и напряжения как элементы, которыми управляют, в ЭЭС;
- показать степень отдаленности запаса от оптимального , используя критерии реальных полных потерь минимума в энергосистеме и отделить реальную зону, оптимизация которой не целесообразна.
Один из вариантов решения является использование информации, полученной от вторых производных специальной функции независимых переменных величин. Алгоритмы, метода минимизации [4] могут быть использованы при решении задач оценки состояния, надежности и поиска оптимального электрического режима в ЭЭС. Вторичная информация полезна в каждом из поставленных задач и вторые производные от некоторой функции системы могут быть обобщенными параметров (ГП). Они будут характеризовать степень изменения режима в данном вопросе предложенного для решения расчетных задач и оптимизации режима в частности оценки ЭЭС надежности и уровня статической устойчивости.
Расчет реальных потерь электроэнергии 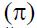 и их производных по мощности
и их производных по мощности 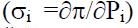 является составной частью запасов планирования электрического режима ЭЭС. Существующие подходы к вычислению основаны на их упрощенном понятии, в котором отражены электрические запасы устойчивости
является составной частью запасов планирования электрического режима ЭЭС. Существующие подходы к вычислению основаны на их упрощенном понятии, в котором отражены электрические запасы устойчивости
Когда сетевой запас далек от статического предела стабильности, тогда id изменяется линейно и использование линейного выражения для 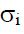 возможно.
Но при подходе к пределу зависимость относительного увеличения становится больше нелинейной [5]. Когда происходит увеличение мощности, происходит увеличение потерь,метод
становится не оптимальным.
возможно.
Но при подходе к пределу зависимость относительного увеличения становится больше нелинейной [5]. Когда происходит увеличение мощности, происходит увеличение потерь,метод
становится не оптимальным.
Таким образом, как обобщенные параметры электрических методов мы можем выбрать вторые производные из системных функций (общие суммы убытков действительной мощности).
Так же к выражению, взятому для коэффициента запаса, мы можем вычислить коэффициент:
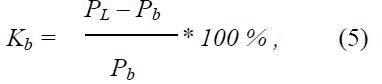
где PL - максимальная произведенная действительная мощность, где Pb - действительная мощность, в котором функция (P) начинает увеличиваться по абсолютной величине. На самом деле граничная точка Pb разделяет зону в / P0, PL / на две зоны. Первая -/P0, Pb /, где функцию P можно линеаризовать; здесь примерно равные приращения соответствуют также равным приращениям П. Вторая - / Рb, PL /, где даже небольшой темп роста угловых характеристик быстро приближается к Р
Поэтому анализ обобщенных параметров режима, сводится к получению коэффициентов запаса, связанные с данной конкретной ситуацией, и с методом по его увеличению Вторые производные от совокупных потерь действительной мощности на реальном (реактивном) потоке, которым управляют, могут быть одним из параметров обобщенного режима. Первая производная действительной мощности потери в сети по параметрам некоторого режима (Di) могут быть получены как [6]:
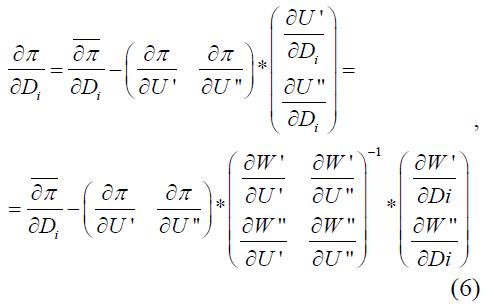
Потом
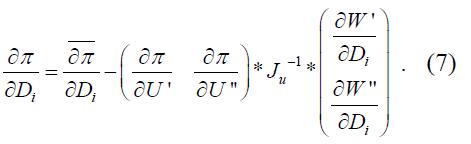
Обозначения
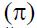 – совокупные реальные потери в сети;
– совокупные реальные потери в сети;
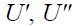 – действительные и реактивные напряжения узлов;
– действительные и реактивные напряжения узлов;
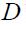 - дифференцированный параметр;
- дифференцированный параметр;
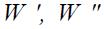 -действительные и реактивные составляющие узлов;
-действительные и реактивные составляющие узлов;
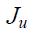 - Матрица Якоби центральных уравнений.
- Матрица Якоби центральных уравнений.
Условие существования производной 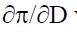 в этом случае будет:
в этом случае будет:
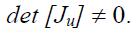
Если det [Джу] равен нолю (режим предела) в таком случае:
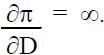
Таким образом режим работы фиксированной системы будет пределом на любом отклонении параметра D, если небольшие изменения этого параметра вызовут неопределенно большие изменения действительных потерь мощности в сети. Граница статической устойчивости может быть определена или из условия (6), или на нулевом пункте детерминанта матрицы Якоби, как от [5] это известно, что те же самые параметры могут быть получены для другой формы отсчета центральных уравнений и матрицы Якоби.
IV. Вычислительный эксперимент
Вычисления проводились для ретроспективной модели Амурской энергосистемы (ЭЭС), связанной с частью китайского ЭЭС. Анализ вычислений был сделан только с проверкой апериодической статической стабильности. Определение ограничения потоков на секции было осуществлено в развес увеличение режима работы (увеличение потока). Главная вычислительная секция включает линию Амур на 220 кВ – Китай, которая обменивается с мощностью на напряжении 110 кВ. Главным узлом управления является узел Амурской ЭЭС.
Амплитуда мощности определяется следующим выражением:
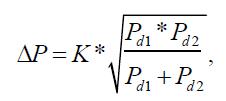
где Рd1 – мощность Амурской энергосистемы;
Рd2 - мощность части китайского ЭЭС;
К = 1,5 регулируемый коэффициент мощности.
Р взят в качестве 14.5 MWt.
Коэфициент запаса Кb, позволяет определить допустимость заданных условий, с учётом 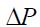
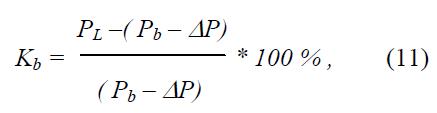
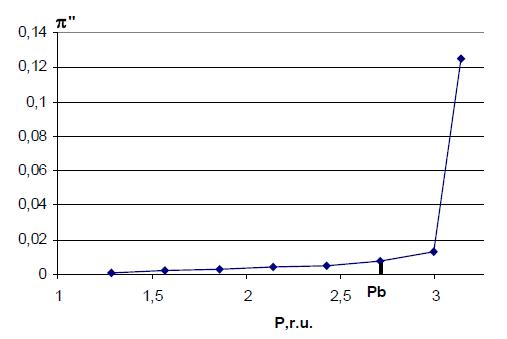
Рис.1 - Кривые второго порядка в действительной системе координат (Р, о.е.).
Результаты вычислений представлены на Рис. 1. Увеличением тяжести режима работы, проходили с увеличением мощности, эти показания вытекают из Амурской ЭЭС связанной с Китайской.
Кb коэффициенты были определены на 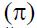 . Конфронтация этих значений позволяет не учитывать уровни напряжения" Амурского "узла в коэффициентах запаса.
Необходимо сказать, что мощность достигает заданного значения желаемого уровня при коэффициенте запаса равном 35%. После этого момента общие потери активной мощности быстро увеличиваются.
Необходимо ограничить мощность или увеличить скорость передачи электроэнергии.
. Конфронтация этих значений позволяет не учитывать уровни напряжения" Амурского "узла в коэффициентах запаса.
Необходимо сказать, что мощность достигает заданного значения желаемого уровня при коэффициенте запаса равном 35%. После этого момента общие потери активной мощности быстро увеличиваются.
Необходимо ограничить мощность или увеличить скорость передачи электроэнергии.
Список литературы
- A. Z. Gamm The market’s simulation of the electric power systems technical service // Energy, 1997. №1. P. 116-122.
- The leading instructions at the power systems’ stability determination. M., 1994. 23 p.
- Idelchik V. I. Calculations and optimization of modes of electrical networks and systems .-M.: Energoatomizdat, 1988 - 288 p.
- The reliability of the energy systems: achievements, problems, prospects / Under edit. of N. I. Voropai. — Novosibirsk: Science. Siberian enterprise of RAS, 1999. – 434 p.
- N. S. Chemborisova Nontraditional parameters of the static stability in the energy systems. Blagoveshensk: publ. of AmSU. 2000. 80 p.
- Fazylov K. F., Nasyrov T. K. Fundamentals of the theory and calculation of steadied electrical systems. Tashkent: Fan, 1985, 74 p.