О некоторых вопросах оценки устойчивости в предельных режимах электроэнергетических систем

Рассматривается задача обеспечения статической устойчивости электроэнергетических систем большой размерности, работающих в тяжелых режимах. Предлагается алгоритм оценки статической устойчивости, основанный на определении полного спектракорней переходных процессов.

Ключевые слова: электроэнергетические системы, устойчивость и предельные режимы электроэнергетических систем.

Переходные процессы в таких динамических объектах, как современные электроэнергетические системы, приобретают в последнее время новые свойства, не имеющие места в системах простой структуры, и представляют собой сложную совокупность колебательных процессов локального и системного характера. Стабилизация низкочастотных колебаний и повышение их демпфирования представляет собой сложную задачу в связи с их общесистемным характером и участием большого числа достаточно мощных генераторов, что требует привлечения соответственно большего числа автоматических регуляторов возбуждения (АРВ) этих генераторов.

Таким образом, необходим всесторонний анализ различных спектров колебаний систем большой размерности при достаточно подробном представлении расчётной схемы. Поскольку расчеты на основе обычных, достаточно простых электрических схем носят ограниченный характер, являются актуальными развитие и применение новых методов, алгоритмов и программ для решения задач статической устойчивости электроэнергетических систем большой размерности в наиболее тяжёлых (предельных) режимах с достаточно подробным учетом основных элементов этих систем.

Рассматривается алгоритм расчёта режимов по апериодической и колебательной статической устойчивости с возможностью детального учета АРВ с известными законами регулирования и настроечными параметрами при заданном способе утяжеления режима. Получившие широкое развитие алгоритмы и программы расчета предельных режимов по апериодической устойчивости, тесно связанные с методами расчетов установившихся режимов, предполагают отсутствиевозможности колебательного нарушения устойчивости и не учитывают детально используемые системы автоматического регулирования.

Для решение ряда эксплуатационных задач необходимучет ограничений, накладываемых на режимы энергосистемы явлениями самораскачивания под действием АРВ-генераторов. Нарушение колебательной устойчивости может происходить в режимах, далеких от предельных по апериодической устойчивости, что неоднократно наблюдалось в действующих электроэнергетических системах. В этой связи необходима оценка предельных режимов не только по апериодической, по и по колебательной устойчивости. До сих пор для оценки предельных режимов по колебательной устойчивости применялись либо частотные методы с построением серии областей Д-разбиения, либо построение траекторий корней переходных электромеханических процессов при утяжелении режима [1]. В обоих случаях требуется большой объем вычислений. Алгоритм автоматизированного поиска предельных режимов по колебательной и апериодической устойчивости, предложенный в настоящей работе, позволяет значительно упростить задачу и сократить время ее решения.

Разработанный алгоритм численного поиска предельныхрежимов по статической устойчивости основан на определении полного спектра корней переходных процессов [1]. На каждом шаге утяжеления рассчитывается установившийся режим и весь спектр собственных значений матрицы коэффициентов линеаризованной системы дифференциальных уравнений переходных процессов в нормальном форме. Критерием достижения предельного режима служит равенство нулю действительной части одного из собственных значений при остальных отрицательных вещественных частях. В алгоритме предусмотрены различные способы утяжеления режима. В основу работы алгоритма положена функциональная зависимость комплексноговектора собственных значений матрицы состояния от заданного параметра утяжеления:

Размерность вектора или число собственных значений зависит от размерности структуры сети и от подробности математического описания элементов системы. Если обозначить

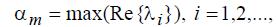
то можно записать уравнение предельного режима:

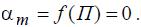(1)

В этом случае обеспечивается заданный критерий предельного режима – действительная часть одного из собственных значений равна нулю, в то время как остальные действительные части меньше нуля. Корень уравнения (1) есть искомый параметр предельного режима 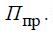. Его определение возможно при использовании итерационных способов расчета корней нелинейных уравнений, например, метода Ньютона или его модификаций [2]. Известно, что сходимость итерационного процесса, основанного на методе Ньютона, сильно зависит от начального приближения и поведения функции (монотонность, гладкость). Эти требования к начальному приближению 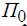и к функции в настоящей задаче могут не выполняться, поэтому для расчета 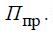предусмотрены два этапа: 1) приближенная оценка параметра утяжеления методом, не чувствительным к поведению функции и обладающим умеренной скоростью сходимости итерационного процесса; 2) точный расчет 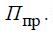помощью модификации метода Ньютона, обеспечивающий быструю сходимость итерационного процесса. На первом этапе можно предложитьспособ определения приращения параметра утяжеления пропорционально значению функции, который применительно к рассматриваемой задаче предпочтительнее традиционных:

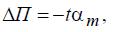
где 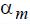– некоторый весовой коэффициент, а знак «минус» учитывает, что в устойчивом режиме 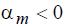, и утяжелению режима отвечает положительное приращение параметра 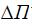. При каждой смене знака 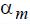коэффициент t уменьшается в два раза, т. е. на i -й итерации k 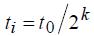, где k – количество смен знака 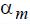за i итераций. Итерационные формулы имеют вид

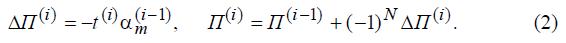
Параметр N определяет направленность утяжеления, например, при утяжелении снижением напряжения

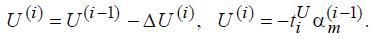
В алгоритме предусмотрен учетпредела апериодической устойчивости, который может быть определен заранее с помощью известных программ [1]. О превышении предела апериодической устойчивости можно судить по вещественному положительному значению 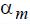, полученному на некотором шаге утяжеления, либо по расходимости итерационногопроцесса расчета режима. В этом случае расчет ведется относительно параметров предшествующей итерации:

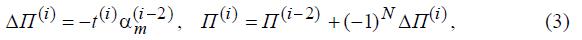
когда 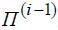и 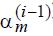соответствуют апериодически неустойчивому режиму.

Усложнение таким способом итерационной процедуры приводит к значительному снижению числа итераций, когда предел колебательной устойчивости близок к апериодическому, связанному с тем, что после превышения предела по апериодической устойчивости значение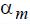 в функции утяжеляемого параметра начинает резко возрастать.

Начальное значение коэффициента t0 может быть принято равным 10...100 % от номинального значения утяжеляемого параметра 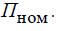. От выбора t0 зависит скорость сходимости итерационного процесса. Если известны параметры предельного режима по апериодической устойчивости, t0 может быть оценено по формуле

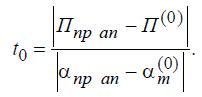
Условием перехода ко второму этапу согласно опыту расчетов, принято неравенств

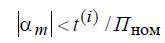
или 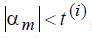, если П измеряется в о.е., 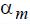– в рад/с. На втором этапе расчета применяется модифицированный метод Ньютона (метод секущих) по параметру, согласно которому [2]

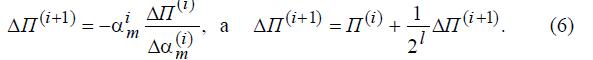
Параметр l зависит от выполнения условия убывания функции

Если это условие выполняется, то l=0 , если нет, то l=1, 2, ... и т. д. до тех пор, пока условие (7) не будет выполнено.

Таким образом, алгоритм для поиска предельных режимов по статической устойчивости состоит в следующем.

1. Задание вида и значения исходного параметра утяжеления .
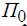2. Задание значения предельного параметра 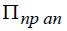условию сохранения апериодической устойчивости.
3. Оценка коэффициента t0 по формуле (4) либо присвоение ему значения (0,1...1).
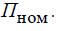4. Расчет установившегося режима и статической устойчивости – всех собственных значений матрицы состояния.
5. Идентификация собственного значения матрицы с максимальной действительной частью.
6. Проверка условия (5). Если условие не выполняется (включая и первую итерацию), расчет параметра утяжеления ведётся по формулам (2) или (3) в зависимости от условия сохранения апериодической устойчивости. При выполнении условия (5) расчет ведётся согласно выражениям (6).
7. Проверка выполнения условия 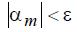., где 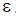.– заданная погрешность расчета. Если условие выполняется, конец расчета, если нет, переход к п. 4. алгоритма.

Предложенный алгоритм обеспечивает быструю и надежную сходимость итерационного процесса к решению, которая обеспечивается при описанной процедуре вычислений фактически в любом случае. Это подтверждается многочисленными расчетами схем электроэнергетических систем различной конфигурации и размерности.

Список литературы

1. Бердник Е. Г., Филиппова Н. Г. Развитие методов и алгоритмов анализа статической устойчивости сложных электроэнергетических систем // Управление режимами электроэнергетических систем: тез. докл. Ивано- во: ИГЭУ, 1995. С. 7.
2. Хэмминг Р. В. Численные методы. М. : Наука, 1972. 400 с