Оценка статической устойчивости регулируемых электрических систем методом малых колебаний в среде прикладного пакета mathcad

Аннотация

Цветов А.С, Ларин А.М. Оценка статической устойчивости регулируемых электрических систем методом малых колебаний в среде прикладного пакета mathcad. В данной работе был предложен метод оценки статической устойчивости методом малых колебаний с помощью математического программного обеспечения и создание на основе этого учебного пособия. Основной проблемой этого вопроса является, необходимость в обеспечении заданного закона изменения регулируемой величины (напряжения) при изменении регулирующей величины (мощности нагрузки).

Общая постановка проблемы

В настоящее время в Украине и весь мир стремятся к повышению качества образования, а также к увеличению уровня самостоятельного дистанционного, образования студентов. Это приводит к необходимости разработки новых методов обучения, которые могут быть реализованы с помощью высокоэффективных современных ком-пьютерных технологий

Одним из важных вопросов подготовки специалистов в области электроэнергетики является анализ поведения электрических систем и систем электроснабжения в исходных установившихся режимах, характеризуемых определенными запасами статической устойчивости [1].

Оценка статической устойчивости регулируемых электрических систем является актуальной задачей электроэнергетики, направленной на выявление параметров, обеспечение заданного закона изменения регулируемой величины при изменении регулирующего параметра, оценки области параметров, при которых электрическая система обладает нормированными запасами статической устойчивости.

Целью работы является создания электронного автоматизированного учебного пособия по изучению методов анализа и оценке статической устойчивости регулируемых электрических систем методом малых колебаний. Оно создается в среде универсальной системы математических расчетов MathCAD, работающей под управлени-ем операционной системы WINDOWS [2].

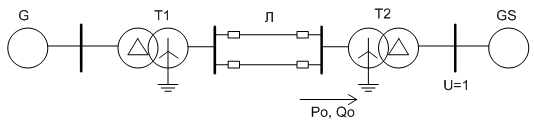
Рисунок 1 - Схема простейшей электрической системы.

В работе в качестве объекта исследований рассматривается простейшая электрическая система, в которой генератор, снабженный автоматическим регуляторов пропорционального типа или сильного действия, выдает мощность в систему бесконечной мощности. Схема такой системы приведена на рис.1.

Чтобы ответить на вопрос устойчива система или нет, необходимо составить математическую модель. Установить в кокой момент и какой характер переходного процесса (апериодический колебательный или возрастающий можно решив или проана-лизировав систему нелинейных дифференциальных уравнений. Весьма удобно это осуществлять на основе линеаризованных уравнений в соответствии с первым методом Ляпунова А.И., который называют методом малых колебаний или отклонений.

Оценку устойчивости будем выполнять в следующей последовательности:

• составляется математическую модель переходных процессов в системе в виде нелинейных дифференциальных уравнений;
• осуществляется линеаризация исходных уравнений;
• составляется характеристическое уравнение или характеристический детерминант, на основании чего можно судить о знаках корней, полученного уравнения;
• на основании анализа корней характеристического уравнения делается вывод оценка статической устойчивости, с помощью критериев, которые определяют знаки действительный корней или знаки вещественных частей комплексносопряженных корней

В среде математического прикладного пакета MathCAD разработано программное обеспечения для автоматизированного определения знаков корней характеристического уравнения с помощью алгебраических критериев (Гурвица, Рауса) и частотных (Найквиста, Михайлова). Определение всей области параметров, в которой электрическая система работает статически устойчиво осуществляется с применением метода D-разбиения в области одного или двух параметров

В качестве примера рассмотрим ЭС с АРВ пропорционального типа

Изменяя параметры системы, можно определить значения минимально необходимого и максимально допустимого коэффициентов усиления регулятора для обеспечения СУ при различных нагрузках. ( рис. 2).

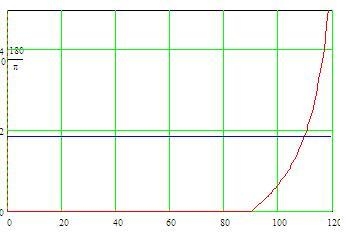
Рисунок 2 - Изменение коєффициентов усиления в зависимости от исходного угла нагрузки

На рис. 3 и рис. 4 показаны характер переходного процесса и годограф Михайлова соответственно. Из анализа приведенных рис. Видно, что при заданных исходных параметрах режима колебательный процесс носит затухающий характер, что соответствует устойчивой системе. Годограф Михайлова при этом также соответствует устойчивой системе. В обеих системах моделирования все элементы представлены блоками. На их базе в системах моделирования была построена схема (рис. 1, 2).

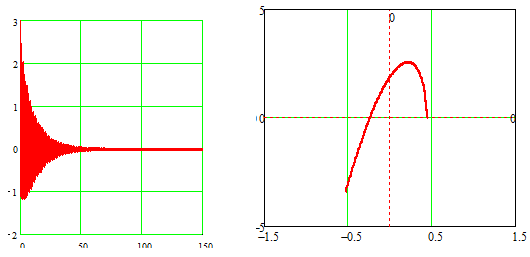
Рисунок 3 - Переходный процесс Рисунок 4-Годограф Михайлова

Таким образом разработка программного обеспечения для определения знаков действительных корней, или действительных частей комплексных корней характеристических уравнений, графическая интерпретация с помощью Mathcad, даёт ряд преимуществ: наглядность, простота, возможность определение устойчивости, не прибегая к дополнительным расчетам.

Список использованной литературы

1. Веников В.А. «Переходные электромеханические процессы в электрических системах» - 4-е изд., перераб. и доп. – Москва «Высшая школа» 1985. – С. 162-230
2. В. П. Дьяконов: Mathcad 11/12/13 в математике. – Москва «Высшая школа» 2007. – С. 315-530.