Электропривод в современном понятии представляет собой сложную электромеханическую систему (ЭМС), для которой характерной особенностью является тесная взаимосвязь процессов в электрической и механической части. Наличие упругих звеньев механической части при взаимосвязи радикально изменяет свойства электропривода в целом и является причиной колебательных явлений в динамике. Колебательные составляющие движения электропривода приводят к отклонению переходных процессов от предписанных технологией и способствуют росту динамических нагрузок на электрическое и механическое оборудование.
Ограничение динамических нагрузок, точное воспроизведение заданных законов движения исполнительных органов машины являются фундаментальными задачами проектирования современного электропривода [1].
Анализ научно-исследовательских работ, опубликованных в технических журналах за последнее десятилетие, показывает на интенсивное продолжение развития теории и практики электромеханических систем с упругими связями.
Приоритетным следует считать направление исследований электромеханических систем с реализацией свойства электропривода демпфировать упругие колебания. Разработаны и используются на практике инженерные методы синтеза упругих электромеханических систем. Которые за счет форми рования динамической жесткости механической ха рактеристики электрпривода обеспечивают оптими зацию электромеханической связи с минимизацией колебательности системы [5, 6].
Метод синтеза ЭМС [2,4], основанный на специфических особенностях электромеханического взаимодействия подсистем с компенсацией сил упругой связи силами инерционной, позволяет достигать предельной степени демпфирования упругих колебаний. При выборе параметров ЭМС по соотношениям оптимального электромеханического © Задорожний Н.А., Задорожняя И.Н., Беш А.Н., 2011 взаимодействия, процессы в подсистемах являются тождественными с минимальной колебательностью координат электропривода и минимальным временем действия динамических нагрузок. Процессы обмена и преобразования энергии упругих колебаний осущест вляются на частоте упругих колебаний. Синтез параметров ТМ1, ТЭ ЭМС производится на основании соотношений взаимосвязи [3].:

которые определяются коэффициентом распределения инерционных масс двигателя и механизма.
Электроприводы с оптимальной электро механической связью или предельным электро механическим взаимодействием имеют параметры эквивалентной замкнутой системы автоматического регулирования, которые выбраны из условия минимизации колебательности, а не обеспечения требуемых показателей точности регулирования.
Поэтому в данной статье решается задача демпфирования упругих колебаний в электроприводах с нулевой статической ошибкой регулирования по скорости и минимальным временем переходных процессов.
Обобщенная структурная схема ЭМС с упругими связями и двухмассовой механической частью приве дена на рис.1. Цепь формирования электромагнитного момента для замкнутой системы автоматического регулирования имеет передаточную функцию:
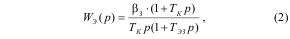

Характеристическое уравнение системы с астатическим регулированием, полученное на основании структурной схемы, для общепринятых обозначений имеет следующий вид:
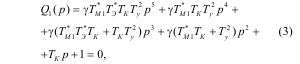
Предельная степень демпфирования упругих колебаний достигается при электромеханической совместимости процессов, когда частота собственных колебаний системы равна парциальным частотам.
Тогда эталонное характеристическое уравнение
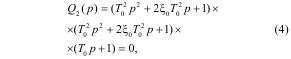
Для общего случая максимума демпфирующего действия электропривода пятый корень характеристического уравнения (3), представленного в форме (4)

Расположение корней характеристического уравнения (3) исходной ЭМС будет соответствовать расположению корней эталонного характеристического уравнения (4) с оптимальными процессами, если коэффициенты одного уравнения Q1(p) при соответствующих степенях оператора «р» приравнять с коэффициентами другого Q2(p). Полученная система алгебраических уравнений совместна и имеет решение при условии, что выполняется следующее соотношение:
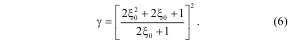
Система уравнений при выполнении условия совместности (6)
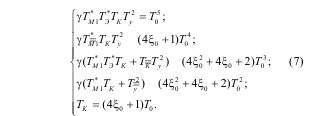
Если выполнить преобразования с подстановкой параметров, найденных из последнего уравнения системы (7) во второе, из второго в первое и делением третьего на четвертое получим соотношения параметров исходной ЭМС в функции показателей качества:
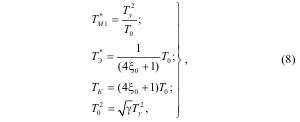
Для общего случая демпфирования упругих колебаний электроприводом из (6) для найдено решение.
Очевидно, что и для системы пятого порядка предельная степень демпфирующего действия электропривода с астатическим регулированием определяется коэффициентом соотношения инерционных масс.


Для типовых (стандартных) настроек регуляторов систем подчиненного регулирования электроприводов с абсолютно жесткими механическими передачами динамические показатели ограничиваются величиной «базовой» суммарной некомпенси руемой постоянной времени контура регулирования
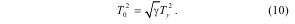
которая эквивалентна всем реальным некомпенси рованным инерционностям [6].
В электроприводе с упругими механическими связями применительно к задаче оптимизации демпфирующего действия эквивалентом «базовой» постоянной времени (11) выступает постоянная

которая задает соотношение (10) для оценки времени регулирования по степени устойчивости

В качестве сравнительных оценок результатов оптимизации ЭМС по типовому критерию – модуль ному оптимуму – с коэффициентом демпфирования 0,707 и критерию «минимум колебательности» 0,707 были сделаны численные расчеты, которые приведены в таблице. Численные значения постоянных времени физически реализуемы и могут быть приняты для настройки контуров регулирования системы автоматического регулирования. Проверка качества регулирования координат электропривода с оптимальными параметрами производилась на математической модели.
Математическая модель ЭМС составлена на основании структурной схемы двухкратноинтегри рующей системы автоматического управления электроприводом в пакете Matlab Simulink. Постоянная времени ТЭЗ* является эквивалентной постоянной интегрирования регулятора тока (мо мента). На основании электромеханической постоянной времени ТМ1* и момента инерции первой массы J1 определено оптимальное значение модуля жесткости механической характеристик электропривода , постоянная времени интегрирования контура регулирования скорости принимается на основании расчета , рассчитаны параметры регулятора скорости. Частота свободных колебаний двухмассовой системы , коэффициент распределения инерционных масс равный 2,0. На рис.2 приведены графики переходных процессов, из которых следует, что система управления обеспечивает предельное демпфирование электромеханических колебаний (идентичность процессов в контуре тока (момента) и в упругой связи механической части Му) при отсутствии статической ошибки по скорости.

Список использованной литературы
1. Чермалых А.В., Майданский И.Я.
Исследование на виртуальной модели режимов
работы электропривода с ПИД-регулятором
скорости // Промислова електроенергетика та
електротехніка. “Промелектро”. – 2005. – № 6.
– С. 27 – 33.
2. Чермалых В.М., Чермалых А.В., Майданский
И.Я., Кузнецов В.В. Исследование динамики и
энергетических характеристик частотно-
регулируемого синхронного электропривода
методом виртуального моделирования // Вісник
Кременчуцького державного політехнічного
університету імені Михайла Остроградського.
– Кременчук: КДПУ, 2009. – Вип. 4/2009 (57),
ч. 1.– С. 112 – 118.
3. Чермалых А.В., Пермяков В.Н., Майданский
И.Я. Исследование динамики экскаваторного
электропривода с помощью виртуальных моделей
// Вісник Кременчуцького державного
політехнічного університету імені Михайла
Остроградського. – Кременчук: КДПУ, 2008. - Вип.
4/2008 (51), ч. 1. – С 48 – 52.