АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
ДИНАМИЧЕСКИХ ПРОЦЕССОВ В СТРУНЕ И ОТВЕСЕ КАНАТА
МОБИЛЬНОЙ ПОДЪЕМНОЙ УСТАНОВКИ

При проведении экспериментальных исследований динамики мобильной аварийно-спасательной подъемной установки АСППУ-6,3 на шахте им. Калинина ГП «Донецкуголь» исследовались динамические и кинематиче- ские параметры подъемной установки в режиме предохранительного торможе ния. Для регистрации этих параметров использовалось три комплекта аппара туры: аппаратура «МАК» ИГТМ НАН Украины для измерения динамических параметров колебаний клети, аппаратура НИИГМ им. М.М.Федорова для фиксации кинематических параметров барабана и характеристики предохранитель ного тормоза, видеоаппаратура для съемки поперечных колебаний струны каната [1].

Предохранительный тормоз включался после разгона подъемной машины до максимальной скорости 2 м/с в режимах спуска и подъема груженой клети. Для анализа было выбрано 6 наиболее характерных фрагментов численных данных – 3 для режима спуска сосуда и 3 для его подъема при различных дли нах каната.

Для каждого процесса торможения было получено три набора численных данных: кинематические параметры барабана и характеристика тормозного усилия, вертикальные ускорения подъемного сосуда и поперечные перемеще ния одного из сечений струны каната. Все данные были синхронизированы и имели временные отметки. Частота регистрации параметров датчиком верти кальных ускорений сосуда составляла 300 Гц, частота регистрации параметров работы тормоза и скорости вращения барабана – 200 Гц, информация о попе речных колебаниях струны каната фиксировалась видеоаппаратурой и в даль нейшем обрабатывалась при помощи программного пакета, частота видеоряда в котором составляет 30 Гц.

Регистрация местоположения клети в момент начала торможения и, соот ветственно, длины отвеса каната проводилась по показаниям указателя глубины подъемной машины, а также проверялась путем интегрирования текущей ско рости вращения барабана. Момент включения предохранительного тормоза фиксировался по исчезновению напряжения в обмотке контактора ТП.

Для синхронизации и последующего анализа были выбраны фрагменты экспериментальных данных, соответствующие процессам торможения, причем продолжительность каждого составляла 13 секунд, из них – 3 секунды до момента включения тормоза и 10 секунд после начала торможения. Синхронизация экспериментальных данных осуществлялась в соответствии с информаци ей датчиков о моменте включения предохранительного тормоза.

При предварительной обработке выбранных фрагментов было проведено сглаживание по методу скользящего среднего с индивидуально подобранными для каждого набора данных параметрами, учитывающими частоты электрических наводок в датчиках и рабочие частоты самих датчиков. При обработке данных о колебаниях струны был выполнен пересчет абсолютного значения отклонения точки струны с учетом расстояния от центра струны до ее сечения, колебания которого фиксировались с помощью видеока меры.

Результаты описанной выше предварительной обработки были сохранены в виде файлов с соответствующими массивами данных. Полный набор обрабо танных результатов представлен в виде семейства графиков на рис. 1 и 2, где начало отсчета времени совпадает с моментом включения предохранительного тормоза.

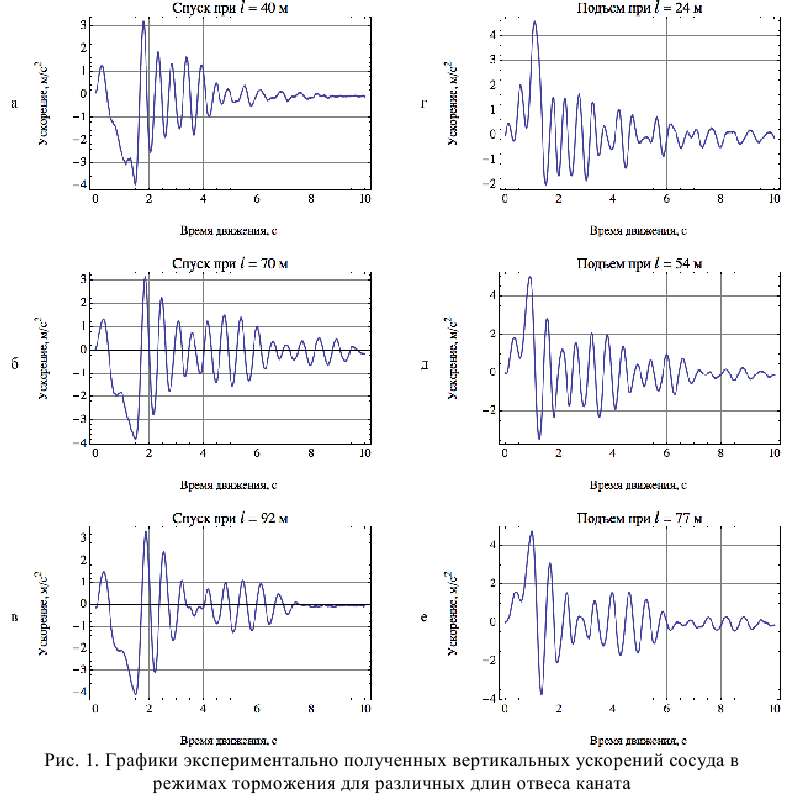
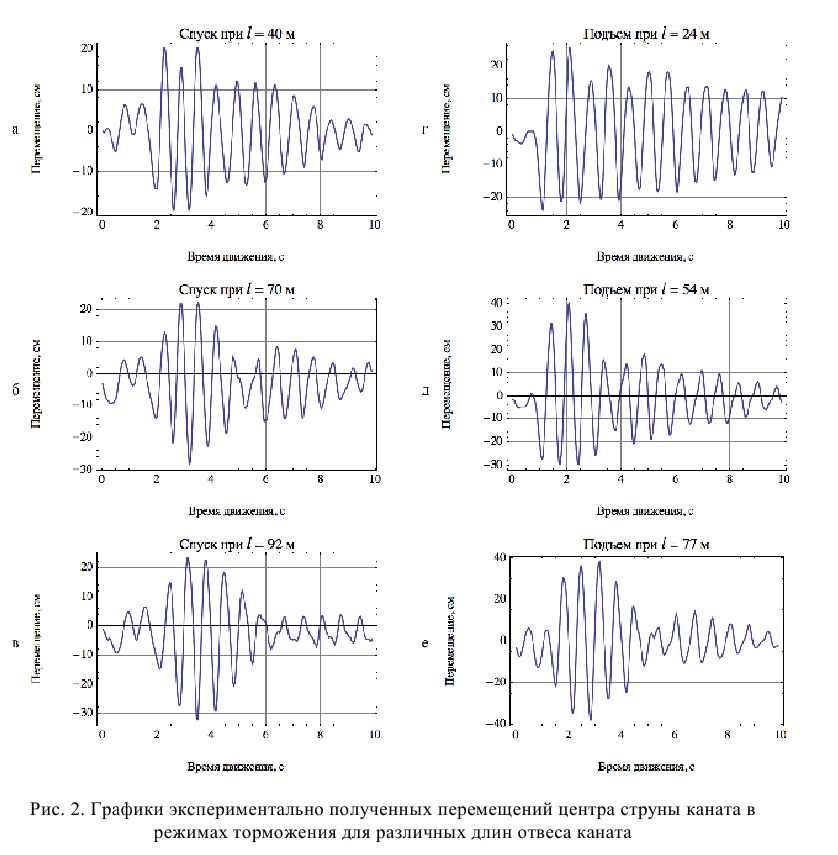
На рис. 1 и 2 фрагменты а - в – соответствуют режимам торможения при спуске груза для длин отвеса каната 40, 70 и 92 м; фрагменты д - ж – режимам торможения при подъеме груза для длин отвеса каната 24, 54 и 77 м.

Анализ полученных фрагментов экспериментальных данных был проведен при помощи различных численных и аналитических методов. Учитывая физическую природу исследуемого процесса – взаимосвязанных гармонических колебаний струны и отвеса каната с грузом, было предложено аппроксимировать как данные измерений вертикальных колебаний сосуда, так и измерений поперечных колебаний струны суммой двух взвешенных затухающих синусоид вида

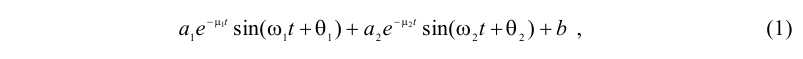
Первое слагаемое отражает «поперечную» составляющую в колебаниях, вызванную поперечными колебаниями струны каната, а второе – «продоль ную», вызванную вертикальными колебаниями сосуда. Независимо от того, в каком элементе каната фиксировались эти колебания (вертикальные колебания нижнего конца каната или поперечные перемещения сечения струны), в обоих случаях, судя по наличию модуляции на большинстве приведенных графиков, присутствуют обе составляющие и их следует учитывать.

Для анализа экспериментальных данных в прикладном математическом пакете Mathematica был реализован программный модуль, который при помощи численного метода наименьших квадратов позволяет найти такие значения на бора параметров – амплитуд, частот, фаз и коэффициентов диссипации, чтобы расстояние между массивом экспериментальных данных и соответствующим массивом значений функции (1) в тех же самых точках было минимальным. В качестве критерия расстояния была взята норма разности этих массивов перво го порядка.

Для параметров функции вида (1) были заданы ограничения, соответст вующие их физическому смыслу и реальным диапазонам их изменения :

Предполагалось, что для реальных параметров подъемной установки час тота ?1 соответствует собственным поперечным колебаниям струны каната, а частота ?2 – собственным вертикальным колебаниям сосуда. Параметр b вве ден для учета погрешности измерительных датчиков и возможного смещения экспериментальных данных относительно 0.

Для обработки в программном модуле были использованы фрагменты полученных экспериментальных данных, соответствующие колебаниям струны и отвеса каната после остановки барабана. Результатом работы программного модуля являются наборы параметров – частот, фаз, амплитуд и коэффициентов диссипации для всех фрагментов экспериментальных данных, соответствую щие колебательным процессам в канате после остановки барабана при различ ных положениях сосуда в стволе.

Для визуальной оценки результатов были получены графики (рис. 3 и 4), построенные с учетом вычисленных значений параметров и отражающие дан ные эксперимента и их аппроксимацию предложенной функцией (1).

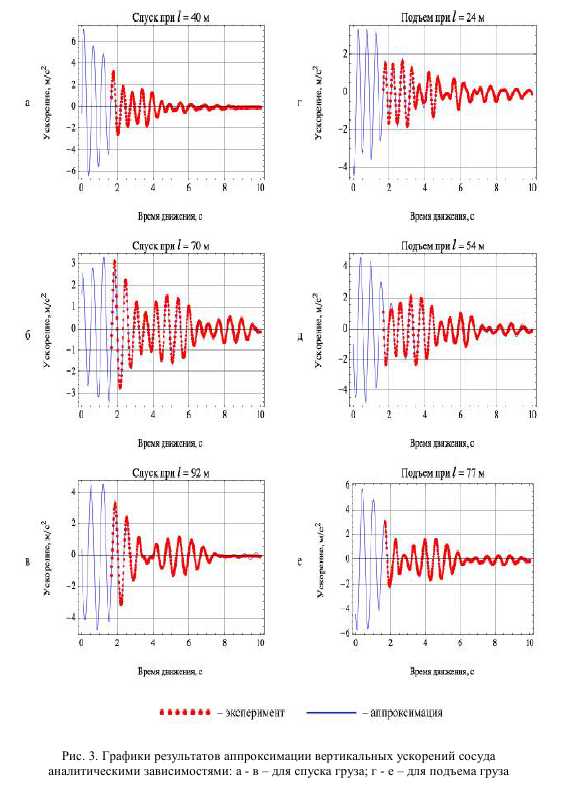
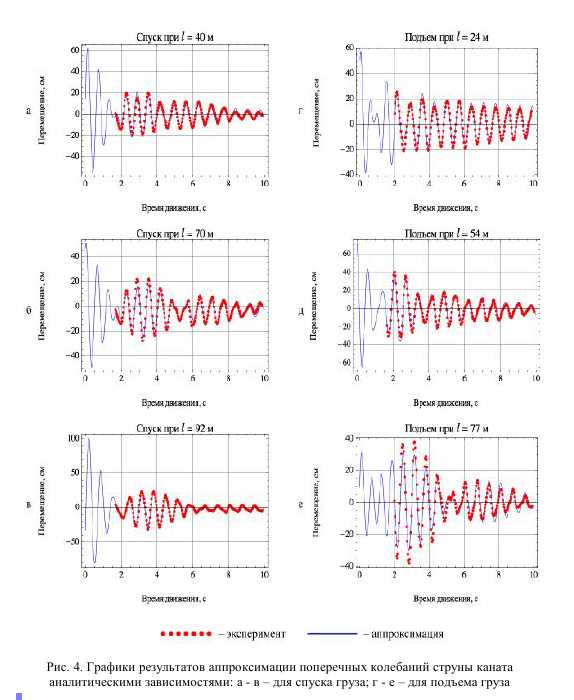
Полученные параметры колебательных процессов в струне и отвесе каната представлены в виде таблицы.

При минимальном отличии частот собственных колебаний сосуда и стру ны каната (длина отвеса 92 м) наблюдается доминирование амплитуды «попе речной» составляющей над «продольной», что приводит к явной модуляции ко лебаний в отвесе каната, вызванных колебаниями струны и соответственно к увеличению коэффициента динамичности.

Также были получены численные значения коэффициентов диссипации для «поперечных» и «продольных» составляющих колебаний в отвесе (µ1= 0,218, µ2= 0,339) и струне (µ1= 0,169, µ2= 0,453) каната как взвешенное среднее коэффициентов диссипации для каждого набора данных.

Найденные экспериментально значения коэффициентов диссипации сле дует использовать в общей динамической модели подъемной установки при ис следовании качественной и количественной картины колебаний системы при торможении [2].

Для проверки полученных значений частот была проведена верификация методом сравнения экспериментально определенных частот вертикальных ко лебаний сосуда с частотами, полученными по формуле Релея как с учетом об щей жесткости системы «струна–отвес–сосуд», так и без ее учета для 6-ти раз личных длин отвеса каната. Отклонения экспериментальных данных от данных, полученных с учетом общей жесткости системы, составили менее 5%, что, в свою очередь, подтверждает корректность проведенных теоретических иссле дований [3,4].

С учетом значений частот колебаний, полученных экспериментально, бы ли рассчитаны значения общей жесткости и приведенной жесткости каната, учитывающие влияние провеса струны каната, а также проведено сравнение этих жестокостей с теоретическими результатами, что характеризуют графики на рис 5. и 6.

Анализ графиков на рис. 5 и 6 свидетельствует о необходимости учета уменьшения полной жесткости системы «струна–отвес–сосуд» за счет прови сания струны каната при определении частот и амплитуд вертикальных коле баний подъемного сосуда.

Таким образом, разработанный метод математического анализа данных, полученных при экспериментальных исследованиях динамики мобильной подъемной установки, заключающийся в аппроксимации их аналитической за висимостью в виде комбинации затухающих синусоид и определении их пара метров подтвердил свою адекватность.

Результаты, полученные при помощи разработанного программного мо дуля, свидетельствуют о тесной взаимосвязи двух различных динамических процессов, таких как поперечные колебания струны и продольные колебания сосуда мобильной подъемной установки.

Судя по соотношениям амплитуд, «поперечная» составляющая колебаний для некоторых длин отвеса каната является доминирующей, что еще раз под тверждает необходимость учета влияния колебаний струны каната при модели ровании динамических процессов, протекающих в канате мобильной подъем ной установки в режимах торможения

Список использованной литературы

1. Ильин С.Р. Экспериментальные исследования динамики мобильной аварийно- спасательной подъемной установки в режиме предохранительного торможения / С.Р. Ильин, С.В. Самуся // Стальные канаты. – 2009. – Вып. 7. – С. 60–65.
2. Ильин С.Р. Математическая модель нелинейных колебаний струны и отвеса каната мо бильной подъемной установки / С.Р. Ильин С.В. Самуся // Наукові праці ДонНТУ. Сер. гірничо-електромеханічна. – 2008. – Вип. 16(142). – С. 122–131.
3. Ильин С.Р. Исследование жесткостных характеристик системы «струна - отвес каната - сосуд» аварийно-спасательной мобильной подъемной установки /С.Р. Ильин, С.В. Самуся // Гірнича електромеханіка та автоматика: Наук.-техн. зб. –2009.–Вип. 82. – С. 142-148.
4. Степанов А.Г. Динамика машин. – Екатеринбург: УрО РАН, 1999. – 392 с