ВВЕДЕНИЕ.
Основным структурным элементом автоматизации современных технологических машин является регулируемый электропривод, в котором интегрированы все технические достижения в области электромашиностроения, силовой преобразовательной электроники, средств систем управле ния и вычислительной техники.
Конструкции механических кинематических цепей приводов имеют тенденцию приближения рабочего органа к электродвигателю, что способствует их упрощению и увеличению жесткости передач при достижении высокой динамической точности отработки заданных движений.
Практически реализовать указанные направле ния совершенствования технического уровня электроприводов не удается изза проявления влияния упругих свойств механических передач, которое способствует развитию колебательных процессов с ростом динамических нагрузок на механическое и электрическое оборудование.
В теории электропривода указывается, что основной задачей электропривода является ограниче ние динамических нагрузок в электромеханической системе и обеспечение заданной точности движения её исполнительных органов. Решить такую задачу возможно на основании системного подхода путем рационального выбора структуры и параметров электромеханической системы при использовании демпфирующего эффекта электропривода.
Демпфирующий эффект электропривода возни кает в результате электромеханической связи, и энергия упругих механических колебаний при определенных условиях рассеивается в диссипативных элементах электродвигателя или возвращается в сеть [1].
АНАЛИЗ ПРЕДЫДУЩИХ ИССЛЕДОВАНИЙ.
Анализ из вестных публикаций по практической оптимизации демпфирующего эффекта в электромеханических системах (ЭМС) свидетельствует, что вопросы синтеза систем при реализации принципов активного подавления упругих колебаний остаются актуальным. Так, для усиления демпфирующего эффекта структур электроприводов с системами подчиненного регулирования требуются дополнительные корректирующие обратные связи. Методика синтеза параметров регуляторов подчиненных контуров при учете упругой механической подсистемы становится громоздкой и аналитическое решение задачи демп фирования колебаний возможно только при упрощении структуры и существенных допущениях. Эффективного демпфирования упругих колебаний удается добиться в электроприводах с системой подчиненного регулирования при предельном быстродействии контура регулирования тока и значениях коэффициента соотношения инерционных масс 2 ≤ γ < 5. Для других областей значений γ демпфирования колебаний электроприводом возможно добиться из менением настройки регуляторов, но при отклоне нии динамической точности и быстродействия от требуемых технологией (то есть оптимальных).
Высокую точность регулирования и требуемое быстродействие при эффективном демпфировании упругих колебаний обеспечивают электромеханические системы управления модальной структуры [2,3].
Синтез электромеханических систем отмеченных структур основан на формировании цепей регуляторов или обратных связей для придания замкнутой системе требуемых динамических свойств по заранее выбранному распределению корней характеристического управления.
ЦЕЛЬ РАБОТЫ.
Синтез электромеханической системы управления привода модальной структуры для обеспечения демпфирования явления упругих колебаний как момента непосредственно в валах механической подсистемы, так и в электрических цепях (тока двигателя).
МАТЕРИАЛ И РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ.
Электроприводы класса машин с существенным взаимным влиянием упругих механических звеньев в ши роком диапазоне собственных частот систем представляют двухмассовой упругой электромеханиче ской системой с обратными связями по координатам первой и второй масс. Обобщенная структурная схема электромеханической системы привода постоянного тока приведена на рис. 1.
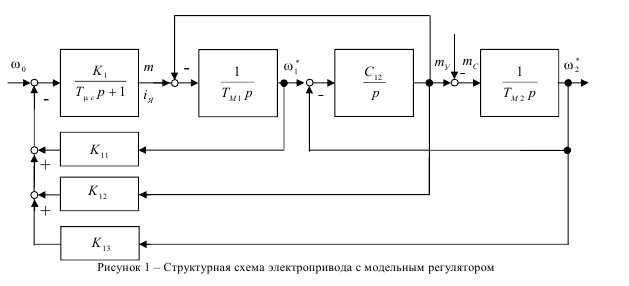
Решение задачи синтеза при общем подходе комплектации корней возможно приведением ха рактеристического уравнения ЭМС к типовым нормированным уравнениям [4], что предполагает не однозначность выбора параметров для обеспечения совместности уравнений. Приемы синтеза ЭМС по нормированным стандартным полиномам не позволяют также выявить механизм (физическую приро ду) влияния отдельных параметров на показатели затухания процессов в электрической (ЭП) и механической (МП) подсистемах.
Широко используемые частототные методы на глядны, но имеют косвенную связь с показателями затухания процессов и довольно громоздки.
Главным и общим недостатком предлагаемых в литературных источниках к практическому применению методов является, что они не учитывают взаимосвязи параметров ЭП и упругой МП, диктуемых наличием физически инерциальной связи [5], и невозможностью явно оценить влияния параметров отдельных подсистем на свойства полной ЭМС.
Простым и практически представительным методом анализа и синтеза ЭМС с упругими связями с целью активного гашения колебаний является метод, основанный на физических закономерностях взаимосвязи и взаимовлияния подсистем и распределением корней характеристического уравнения по принципу электромеханической совместимости [3].
Для основных координат электропривода считаются известными передаточные функции по возмущающему и управляющему воздействиям:

В характеристическом уравнении (3) приняты следующие обозначения:К1 = КР· КП коэффициент передачи прямого канала, включающий регулятор и преобразователь; К11, К12, К13 коэффициенты обратных связей по скорости первой массы, упругому моменту, скорости второй массы.
Оценить демпфирующие свойства электромеханической системы достаточно по расположению корней характеристического уравнения. Оптимальное демпфирование упругих механических колебаний достигается при предельном электромеханиче ском взаимодействии подсистем, которое зависит от коэффициента взаимодействия:

и электромеханического демпфирования собственно активного элемента ЭП (двигателя):

Характеристическое уравнение (3) при записи его в форме показателей электромеханического взаимодействия (4), (5) будет иметь следующий вид:
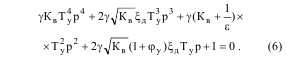
В характеристическом уравнении для удобства преобразований и расчета значений физических параметров ЭМС введены дополнительно обозначения:

В зависимости от конкретных ЭМС, параметров и степени реализации демпфирующего эффекта коэффициенты обратных связей могут принимать как положительные, так и отрицательные значения.
В результате электромеханической связи в консервативную МП (без диссипации энергии) вносится
из ЭП демпфирование, и колебательные процессы в подсистемах по характеру будут тождественными, но с различной огибающей, что соответствует представлению характеристического уравнения (6) в виде
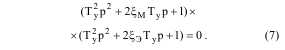
Предельная степень демпфирования упругих механических колебаний (момента в валах) и электрических цепях (тока в обмотке якоря) достигается при динамической равнозначности процессов в МП и ЭП.
После преобразования характеристического уравнения (7) и сравнения его коэффициентов при соответствующих степенях с характеристическим уравнением в форме обобщенных показателей (6), получаем условия оптимизации ЭМС по критерию предельного затухания колебаний:

Для реального сочетания параметров при выполнении условий (8), (9) электропривод представляет собой активное демпфирующее звено, свойства которого реализуются при колебательных процессах в электрической подсистеме.
Предельная степень демпфирования в ЭМС достигается соответствующим выбором параметров по соотношениям, которые получены при совместном рассмотрении системы из выражений (4) и (5):

При подстановке в (10), (11) условий оптимизации (8), (9) можно установить соотношения для расчета коэффициентов обратных связей и базовой величины постоянной времени, которая характеризует инерционность прямого канала регулирования:
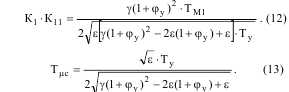
Пользуясь соотношениями (12), (13), можно синтезировать параметры ЭМС по критерию минимума колебательности координат и расчет выполнить, придерживаясь следующего порядка:
Динамические свойства элементной базы современных систем управления и допустимые границы коэффициента для динамичных приводов машин с реальными параметрами объектов управления показывают, что коэффициент веса:
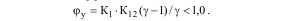
Глубина обратной связи по скорости первой и второй масс для обеспечения условий устойчивости может корректироваться коэффициентом
(13) вычислить оптимальные параметры цепей обратных связей по координатам первой и второй масс К11, К12, К13,
- полученные значения оптимальных параметров должны удовлетворять условиям физической реализуемости. Если реализовать значения коэффициентов не удается, требуется компромиссное решение с вариацией параметров не только электриче ской подсистемы, но и упругой механической под системы.
Для иллюстрации практического исполнения методики синтеза ЭМС модальной структуры были рассчитаны оптимальные коэффициенты и постоянная времени (12), (13) для электромеханической системы регулирования скорости клети непрерывного заготовочного стана КМК со значениями параметров ТМ1 = 0,945 с; ТЭ = 0,065 с; К1 = 12,32 . Процессы пуска и захвата металла валками клети моделировались по структурной схеме в среде пакета Matlab Simulink и приведены на рис. 2.
Осциллограммы машинного расчета показывают, что система обеспечивает предельное демпфирование упругих колебаний в электрической и механической подсистемах при высокой статической и ди намической точности поддержания скорости.
ВЫВОДЫ.
Предлагаемая методика проста, удовлетворяет требованиям системного анализа, имеет прозрачное физическое содержание. Синтез параметров электромеханической системы управления и регулирования модальной структуры позволяет реализовать благоприятное свойство активного гашения электроприводом упругих колебаний.

Список использованной литературы
1. Ключев В. И. Теория электропривода: Учеб-
ник для вузов. – М.: Энергоатомиздат, 1985. – 560 с.
2. 2. Бургин Б.Ш. Анализ и синтез двухмассовых
электромеханических систем: Монография / Ново-
сиб. электротехн. ин-т. – Новосибирск, 1992. – 199 с.
3. Задорожний Н.А. , Задорожняя И.Н. Корневые
оценки качества регулирования электроприводов со
свойствами электромеханической совместимости //
Вестник НТУ ХПИ, вып. 12, том 2. - Харьков: НТУ
ХПИ, 2002 – С. 445-447.
4. Марущак Я.Ю. Синтез електромеханічних си
стем з послідовним та паралельним коригуванням:
Навч. посібник. – Львів: Видавництво Нац. унів-ту
Львівська політехніка, 2005. – 208 с.