В настоящее время в Украине на вооружении горноспасательной службы находится пока единственная в стране мобильная подъемная установка, пред назначенная для проведения аварийно-спасательных работ в стволах угольных шахт. Опыт практической эксплуатации установки при ликвидации последст вий аварий в стволах, в частности, на шахте им. Карла Маркса ГП «Орджони кидзеуголь» в 2008 г. показал ее высокую эффективность и одновременно вы явил ряд новых технических проблем, которые не присущи стационарным подъемным установкам.
Эти проблемы вызваны тем, что место размещения подъемной машины можно выбрать только там, где есть свободный подъезд к копру. В некоторых случаях это приводит к увеличению длины струны каната до 100 м и более. При такой длине из-за того, что масса груженой спасательной клети не превышает 2800 кг, статический провес струны может достигать 2,5 м, а амплитуда коле баний при торможении – 3–5 м. Это создает реальную опасность схода каната со шкива, его ударов по элементам нижерасположенных шахтных конструкций с последующим разрушением проволок каната.
Взаимовлияние динамических процессов в струне и отвесе каната осо бенно ощутимо проявляется при использовании входящего в комплект обору дования отклоняющего шкива диаметром 1м с приведенной массой, значитель но меньшей по сравнению с массой стационарного копрового шкива. Поэтому в соответствии с разрабатываемыми проектами применения мобильных подъем ных установок канат приходится заводить через дополнительное отверстие в стенке копра. Размеры этого отверстия необходимо определять с учетом мак симально возможной амплитуды колебаний струны в экстремальных режимах торможения.
Динамические характеристики колебательных процессов в подъемном канате определяются массовыми, геометрическими и жесткостными парамет рами всей механической системы подъемной установки и настройкой тормоза (характеристика тормозного усилия, его кратность, время холостого хода). Та ким образом, задача исследования взаимной зависимости для реального много образия сочетаний параметров, присущих именно мобильной установке, и оп ределения допустимых значений параметров настройки тормоза в зависимости от фактических жесткостных параметров системы для реально возможных ва риантов размещения установки около ствола, является актуальной.
Общая нелинейная математическая модель динамики системы «машина – струна – отвес каната – сосуд» описана в работах [1,2], где отмечено, что дан ной системе присуще явление возникновения внутренних резонансов с не сколькими зонами неустойчивости по глубине ствола, в которых происходит раскачивание струны и подъемного сосуда с периодическим ростом амплитуд колебаний обеих упругих звеньев типа «биения».
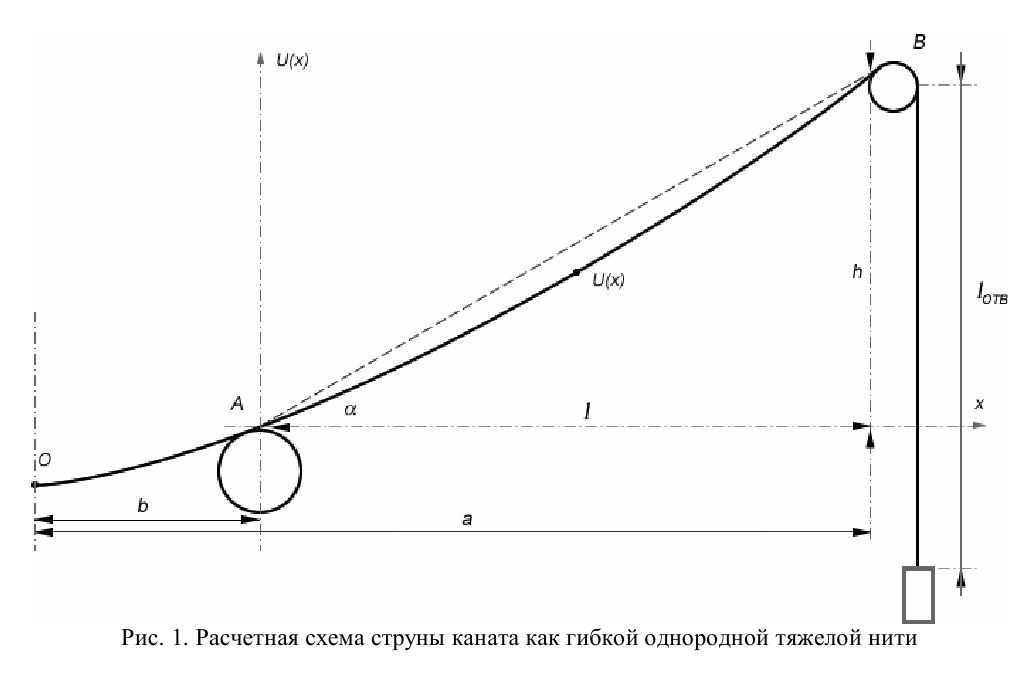
Амплитуды и устойчивость этих колебаний существенно зависят от об щей жесткости всего каната со струной для каждой точки ствола, в которой происходит торможение. Для исследования зависимости этих колебаний от длины и угла наклона струны, длины отвеса каната рассмотрим струну каната подъемной установки как гибкую однородную тяжелую нить [3].
Расчетная схема такой математической модели представлена на рис. 1, где h и l соответственно расстояния по вертикали и горизонтали между точка ми набегания струны каната на барабан А и сбегания с копрового шкива В.
Данная система обладает двумя модами колебаний. Первая соответствует поперечным колебаниям струны с сосудом, подвешенным на абсолютно жест ком отвесе каната, вторая – чисто упругим колебаниям отвеса каната с сосудом.
В работе [3] приведено уравнение статической формы струны в виде цепной линии :
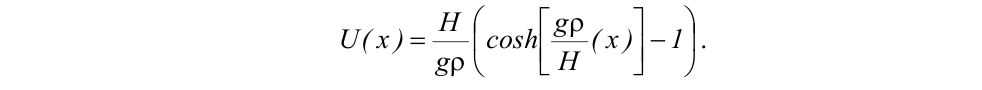
В расчетной схеме положим начало системы координат в точке О, которая характеризует самое нижнее положение гибкой нити. Для рассматриваемо го случая точка О находится за пределами струны каната.
Рассчитаем длину струны каната с учетом ее провеса. Допустим, что сила натяжения в струне

где Q – вес концевого сосуда; lотв – длина отвеса каната; g – ускорение свободного падения.
Обозначив коэффициент, характеризующий отношение массы гибкой тяжелой нити к ее натяжению, как
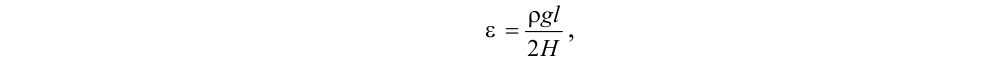
определим расстояние от точки О до точки набегания каната А на барабан:

Тогда уравнение интересующей насчасти провеса каната АВ будет иметь следующий вид :
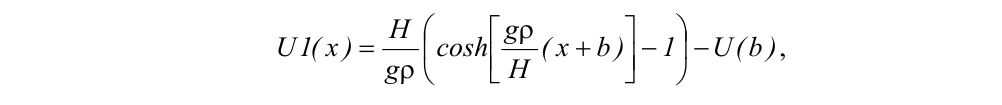
а длина струны каната АВ
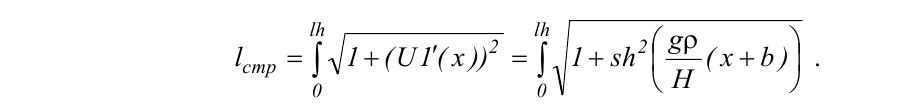
Вычислив этот интеграл, получим
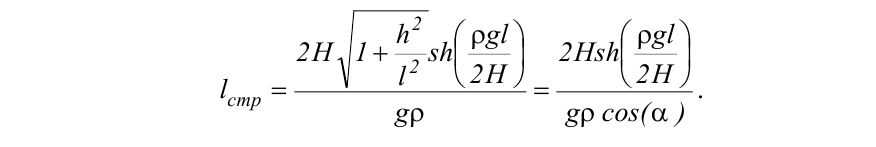
Эквивалентная жесткость струны каната, зависящая от его провеса, вычисляется как отношение приращения силы натяжения к приращению удлинения каната, т.е.
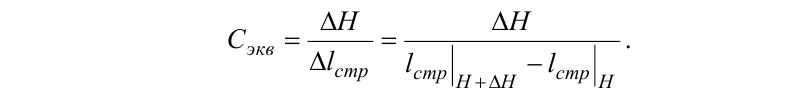
Вычисляя предел при как

получим
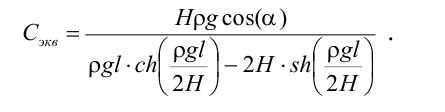
В модели дискретного аналога [1]. при чисто продольном растяжении приведенная к точке подвеса сосуда жесткость каната определяется как
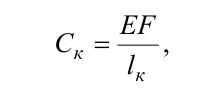
где EF – жесткость каната с равномерно распределенной массой на растяжение; При колебаниях системы «струна – отвес каната – сосуд» последовательно с упругим растяжением каната в отвесе и в струне включается в работу второе упругое звено - «струна», которое за счет изменения длины провисающей части струны путем перебегания через отклоняющий шкив увеличивает (уменьшает) перемещение конца каната с сосудом при увеличении (уменьшении) растягивающе го усилия. Поэтому общая жесткость системы «струна – отвес каната – сосуд» в модели дискретного аналога определяется по формуле последовательного соединения жест костей
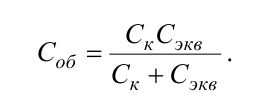
Для построения графиков полученных зависимостей проведем вычислительный эксперимент с параметрами, соответствующими реальному размещению мобильной подъемной установки АСППУ-6,3 на шахте им К.Маркса ДП «Орджоникидзеуголь» со следующими параметрами: масса груженой бадьи Q = 620 кг, линейная плотность каната v = 2,44 кг/м, длина отвеса каната lотв изменяется от 40 до 1000 м.
Для случаев, когда длина отвеса будет фиксирована, примем lотв =140 м, для случаев, когда будет фиксирован угол наклона струны каната, примем 15град.
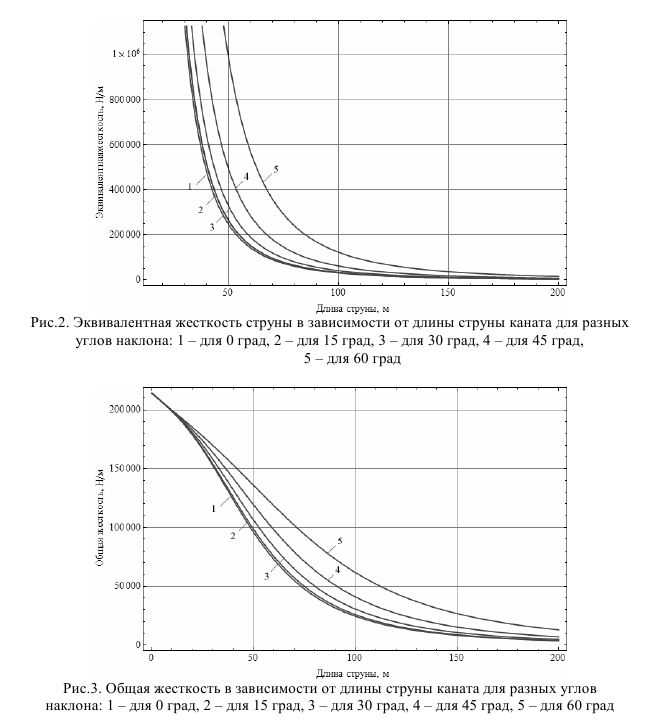
На рис. 2 и 3 изображены зависимости эквивалентной и общей жесткостей струны каната от длины струны для разных значений углов наклона.
Введем параметр – приведенная к точке подвеса сосуда общая продольная жесткость системы
, которая эквивалентна по своим упругим характеристикам системе струна – отвес каната – сосуд
.
Этот параметр, изменяющийся в зависимости от длины каната, позволяет представить систему в виде одномассовой модели и с достаточной для практики степенью точности определить зависимости первой частоты колебаний сосуда от геометрических и массовых параметров системы по формуле Рэлея:
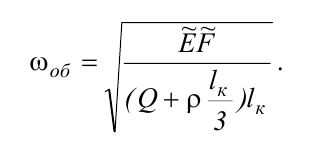
На рис. 4 и 5 показаны зависимости значения общей жесткости от положения сосуда в стволе для разных длин струны каната.
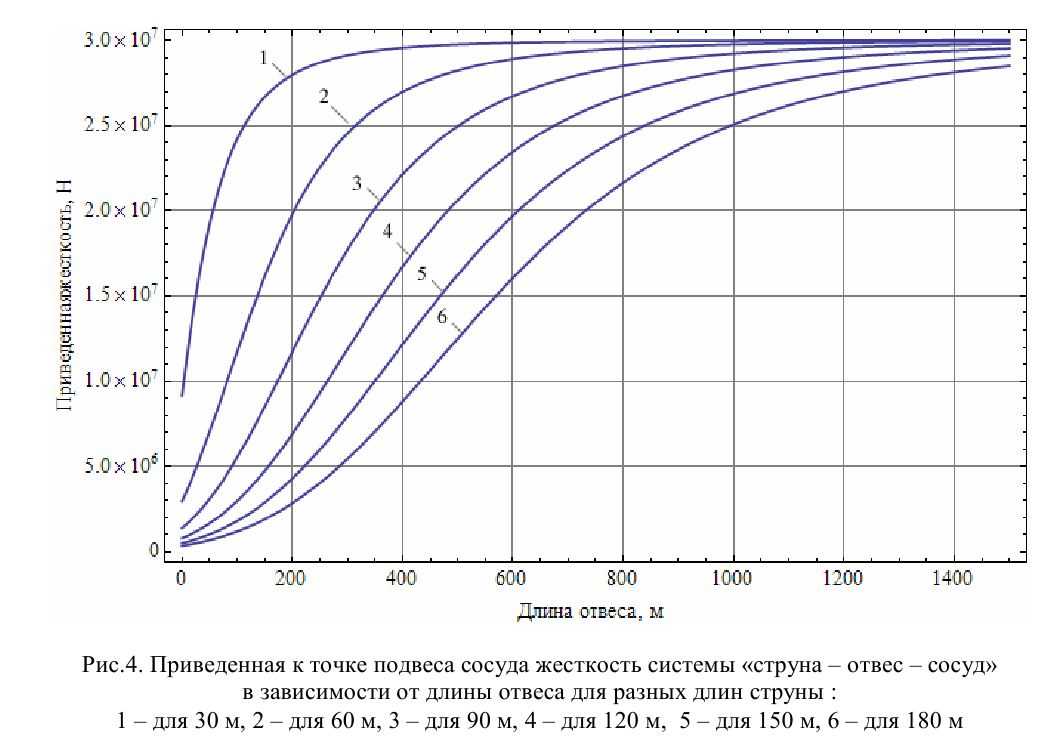
Из приведенных графиков видно, что увеличение длины отвеса каната при опускании подъемного сосуда в стволе ведет к увеличению эквивалентной жесткости струны за счет уменьшения ее провеса. При этом продольная жесткость каната уменьшается с увеличением натяжения, что приводит к появлению экстремума на графике общей жесткости системы. Однако при нахождении сосуда на большой глубине общая жесткость системы уже незначительно отличается от продольной жесткости упругого каната без учета провисания струны.

Анализ полученных результатов говорит о существенном влиянии эквивалентной жесткости струны на общую жесткость каната подъемной установки,
и соответственно на протекание динамических процессов в системе струна –
отвес каната – сосуд
.
Значительное влияние струны каната на динамику системы является негативным фактором, который надо учитывать на стадии разработки проектов
применения мобильной подъемной установки при аварийно-спасательных работах в шахтных стволах.
Результаты дальнейших исследований позволят разработать рекомендации по обоснованию и выбору рациональных режимов эксплуатации и параметров размещения мобильных подъемных установок для различных условий их применения на конкретных шахтных стволах с учетом взаимовлияния колебательных процессов в струне и отвесе каната в режимах торможения.
Список использованной литературы
1. Ильин С.Р. Самуся С.В. Математическая модель нелинейных колебаний струны и отвеса
каната мобильной подъемной установки // Наук. праці ДонНТУ. Сер. гірничо-електромеха-
нічна. – 2008.– Вип. 16(142). –С.122-131.
2. Самуся С.В. Ильин С.Р. Экспериментальные исследования динамики мобильной аварий
но-спасательной подъемной установки в режиме предохранительного торможения // Сталь
ные канаты. – 2009.–Вып. 7.– С. 60-65.
3. Степанов А.Г. Динамика машин. – Екатеринбург: УрО РАН, 1999. – 392 с.