УДК 62-83:621.314.2 К.П. Здрозис

ПОВЫШЕНИЕ КАЧЕСТВА ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ С РЕГУЛИРУЕМЫМ АСИНХРОННЫМ ЭЛЕКТРОПРИВОДОМ.

Розглянуто засіб зниження коливань двомасовой ЕМС механізму підйому з замкнутою системою електропривода ТПН-АД за рахунок введення від'ємного зворотного зв'язку за різницею швидкостей обох мас. Одержано вираз для розрахунку оптимального коефіцієнта зворотного зв'язку, наведено розрахункові графіки перехідних процесів, що ілюструють ефект корекції.

В работе [2] была показана возможность и целесообразность использовать для многих подъёмных механизмов кранов асинхронный электропривод с тиристорным преобразователем напряжения (ТПН-АД). Там же произведен анализ показателей качества двухмассовой электромеханической системы (ЭМС) подъёмных механизмов, когда для регулирования их скорости используется отрицательная обратная связь по скорости двигателя w1. Как это следует из работы [3] и нашло своё численное подтверждение в работе [2], у таких механизмов, характеризуемых небольшим отношением второй массы к первой, коэффициент демпфирования очень мал и потому колебательность такой ЭМС велика.

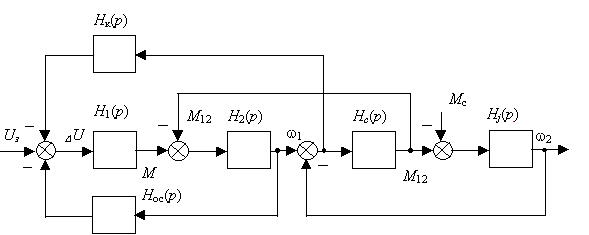
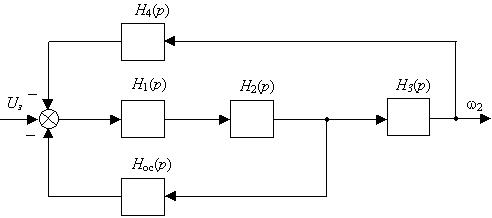
Для принудительного демпфирования колебаний ЭМС подъёмных механизмов в систему целесообразно вводить коррекцию -отрицательную обратную связь по разности скоростей обеих масс [1]. Структурная схема двухмассовой ЭМС с замкнутой системой электропривода и с коррекцией, где Нос(р) = Кос и Нк(р) = Кк, приведена на рис.1. На ней Н1(р) - передаточная функция электрической части: регулятора с коэффициентом Ку, ТПН - с Ктп и электромеханический преобразователь АД, после линеаризации характеризующийся коэффициентом Кд;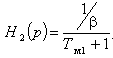

где 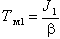- электромеханическая постоянная времени, b - жёсткость механической характеристики, J1 - первая масса ЭМС (ротор двигателя).

(1)

) где С12 - жёсткость упругой связи, J2 - момент инерции второй массы (груза).

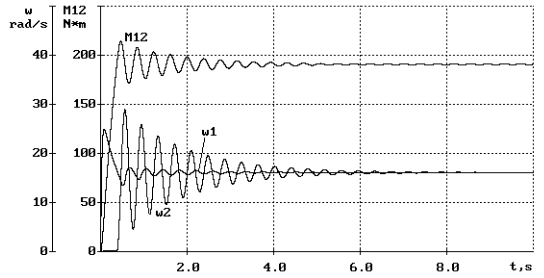
Рассмотрен способ снижения колебательности двухмассовой ЭМС механизма подъёма с замкнутой системой электропривода ТПН-АД введением отрицательной обратной связи по разности скоростей обеих масс. Выведено выражение для расчёта оптимального коэффициента обратной связи, приведены расчётные графики переходных процессов, иллюстрирующие эффект коррекции

The paper presents the method of vibration reduction of double mass electromechanical systems if thyristor voltage converter for induction motor with speed feedback is used. The second feedback is proposed. It included to difference between speeds of two masses of mechanical part. The formula for calculation of the best gain factor value of this feedback is obtained.

















©Здрозис К.П.,2000

Преобразуем эту структурную схему, перенеся точки съёма внутренней обратной связи по моменту упругой деформации М12 и корректирующей обратной связи по ходу действия сигнала к точке с координатой w2, а точку приложения первой связи против хода сигнала. Тогда получаем структуру, приведенную на рис.2.

Рис.2. Структурная схема после преобразования.
В ней:

Для схемы рис.2 передаточная функция определяется как:

Подставив в передаточную функцию (3) выражения из (2) и (1) получаем окончательно

Характеристическое уравнение, соответствующее (4):

Здесь

- электромеханическая постоянная времени абсолютно жёсткой системы,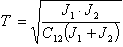

- постоянная времени двухмассовой ЭМС,

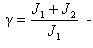- коэффициент соотношения масс [1].

Считая КS заданным, зависящим от требуемой жесткости механических характеристик, определим выражение для вычисления такого значения коэффициента Кк которое обеспечивает максимальное демпфирование. Для этого характеристическое уравнение (5) перепишем в виде, чтобы свободный член равнялся единице:
(6)

а стандартную форму характеристического уравнения звена третьего порядка запишем следующим образом:

или

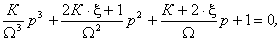
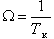где - частота колебаний колебательного звена, а - коэффициент, характеризующий соотношение между постоянными времени инерционной и колебательной составляющими.

Приравнивая коэффициенты при соответствующих степенях р характеристических уравнений (6) и (7), получаем три уравнения:

(8)
(9)
(10)

Исключая W при совместном решении (8) и (10), получаем

(11)

Для нахождения оптимального значения К, при котором коэффициент демпфирования становится наибольшим, решим уравнение:

(12)

что даёт

Решение тех же уравнений после исключения К дает:

(13)

Аналогично получаем выражение для оптимального значения частоты:

(14)

Подставляя (12) в (11) или (14) в (13), находим выражение:

(15)

Интересующую нас величину коэффициента коррекции Кк, обеспечивающую наибольшее демпфирование колебаний, можно рассчитать по формуле, которая является решением уравнения, полученного подстановкой выражений (12),(14) и (15) в (9):

или

(16)

Итак, для заданной рабочей точки механической характеристики необходимой жесткости, для которой известны КS и Тм, по (16) следует найти значение Кк доставляющее максимум коэффициенту демпфирования со значением, рассчитываемым по (15). При этом следует четко представлять, что повышение жесткости механических характеристик уменьшает оптимальное значение Кк, и что важнее, существенно снижает xmax .

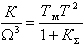
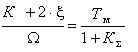
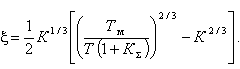
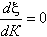
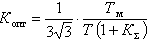
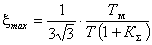
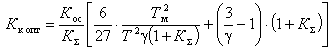
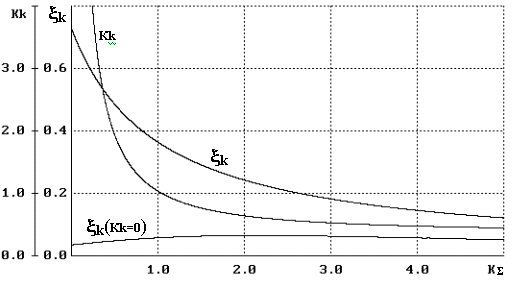
На рис. 3 показаны зависимости , обеспечиваемые при соответствующих значениях Кк по (16), из которых следует, что абсолютные значения xmax снижаются от 0,7-0,8 в разомкнутой системе до 0,1 и меньше при высокой жесткости.

Рис. 3. Расчётные зависимости xк и Кк опт от КS для S = 0,85

Для иллюстрации поведения системы при действии коррекции были проведены соответствующие расчёты для ЭМС механизма подъёма крана с двигателем типа 4МТF/H/160LB6, мощностью 15 kW.Расчётные параметры ЭМС, приведенные к валу двигателя

Расчётные параметры ЭМС, приведенные к валу двигателя:

J1=0,35 kgm2 , J2=0,097 kgm2 , C12=25,2 Nm

На рис.4 приведены расчётные осциллограммы переходных процессов этой ЭМС для Ку = 1,3 без коррекции (Кк = 0), а на рис.5 при действии оптимальной коррекции (Кк опт = 0,618). Из них следует, что вследствие роста демпфирования при введении коррекции (xк = 0,23 вместо 0,065) перерегулирование по скорости снижается с 85% до 15%, а по моменту упругости - с 12% до 5,5%.

Аналогичные расчёты были выполнены для той же ЭМС, но большего в 3 раза коэффициента усиления Ку, обеспечивающего более высокую жёсткость механических характеристик. Они показали, что колебательность несколько выше при использовании соответствующего значения Кк опт = 0,426: так, перерегулирование по скорости достигает 20%, а по моменту -7%.

Рис. 4. Расчётные зависимости переходного процесса ЭМС подъёма без коррекции (Кк = 0).

Рис. 5. Расчётные зависимости переходного процесса ЭМС подъёма с коррекцией (Кк опт ).

Таким образом, введение корректирующей связи по разности скоростей обеих масс при правильном выборе коэффициента коррекции Кк в пределах (0,9 …1,25) Кк,опт приводит к существенному улучшению переходного процесса ЭМС механизма подъема.

Список использованной литературы.

1. Герасимяк Р.П., Аит А.М., Рамарувахуака А.М. Синтез электромеханической системы подъёмных механизмов с подавлением упругих колебаний // Електромашинобудування та електроустаткування: Респ.міжвід.наук. - техн.зб. - 1996. - Вип.48. - С.30-37.
2. Герасимяк Р.П., Здрозис К.П. Показатели качества электромеханических систем подъёмных механизмов с синхронным электроприводом. Вісник ХДПУ. Збірка наукових праць. Тематичний випуск 113. - Харків, ХДПУ, 2000. - С.159-161.
3. Ключев В.И. Теория электропривода. М.: Энергоатомиздат, 1985.-560с.

Получено 14.10.00