Bakalov V.A., Sivokobylenko V.F. Perfection of mathematical model of electric station. In paper the general description of the computer program is given. The duty of its mainframes is described. The developed mathematical model of electrical station allows to investigate behavior of generators at various kinds of short circuits. The differential equations of the shunt are given. With its help the short circuits are simulated. The results of account of dynamic stability of the generator are submitted.
Целью данной работы является совершенствование математической модели электрической станции, разработанной в [1], в части возможности задания различного способа соединения элементов в главной схеме вместо предусмотренной схемы жесткой структуры.
Расчетную схему электрической станции удобно разделить на ряд однотипных элементов, описываемых своими наборами дифференциальных и алгебраических уравнений. Каждый элемент характеризуется набором входных и выходных параметров, которые полностью описывают всю совокупность процессов внутри каждого элемента и его влияние на другие элементы расчетной схемы. Представление элементов схемы в форме полных дифференциальных уравнений позволяет получить мгновенные значения токов и напряжений, благодаря чему может быть выполнен анализ устройств релейной защиты и автоматики, динамической устойчивости генераторов.
В расчетной схеме электрической станции можно выделить следующие ее типовые элементы, соединяемые по заданной структурной схеме:
Исходная модель [1] имеет недостаток, заключающийся в том, что расчеты можно проводить только для схем, содержащих три блока. Каждой блок состоит из генератора, блочного трансформатора, рабочего трансформатора собственных нужд и по одному эквивалентному асинхронному и синхронному двигателю для моделирования нагрузки собственных нужд. В ряде случаев требуется увеличение количества блоков станции и других элементов схемы. Например, на ряде АЭС блоки содержат по два рабочих трансформатора собственных нужд, подключенных к выводам генератора, а при расчетах режимов пуска или группового самозапуска электродвигателей собственных нужд возникает необходимость учета отдельных двигателей.
Для устранения этого недостатока предложено изменить структуру программы. Названные выше элементы оформлены в виде отдельных объектов. Каждый из них описывается в двух массивах: массиве исходных параметров и массиве связей. В результате появилась возможность моделировать схемы различной структуры, как электростанций, так и других объектов, задавая необходимое количество генераторов, двигателей, линий электропередачи и трансформаторов.
Это также позволило исследовать переходные процессы при симметричных и несимметричных коротких замыканиях в любом заданном узле схемы, а также режимы пуска и самозапуска двигателей, при автоматическом повторном включении после перерыва питания.
Имитация коротких замыканий достигается за счет использования активно-индуктивного шунта с соединением его ветвей в треугольник. Шунт описывается следующими дифференциальными уравнениями:
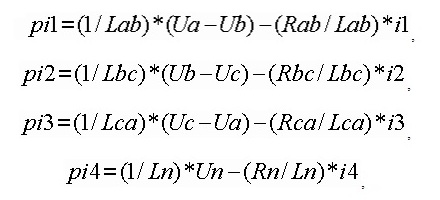
где: Lab, Lbc ,Lca ,Ln- индуктивности ветвей шунта, Rab, Rbc, Rca, Rn-активные сопротивления ветвей шунта, i1, i2, i3, in-токи ветвей, Ua ,Ub, Uc- фазные напряжения в месте подключения шунта, Un- напряжение фазы А, либо фазы которая замыкается на землю.
При коротких замыканиях на землю скачкообразно уменьшаются Ln и Rn, а при междуфазных коротких замыканиях уменьшаются: Lab, Lbc ,Lca , Rab, Rbc, Rca.
Реализованная программа исследования электромеханических переходных процессов в сложных многомашинных системах состоит из четырех блоков.
В первом блоке задаются исходные данные. К ним относятся параметры элементов схемы, схема соединения элементов, заданные продолжительность и вид коротких замыканий. Во втором блоке определяются токи в ветвях линии электропередачи, блочного трансформатора, автотрансформатора, трансформатора собственных нужд, потокосцепления контуров схем замещения электрических машин, напряжения возбуждения синхронных генераторов и двигателей, а также напряжения в узлах схемы.В третьем блоке определяются текущие значения параметров режима. Для этого решаются дифференциальные уравнения элементов схемы. Для решения дифференциальных уравнений необходимо знание напряжений в узлах схемы. Последние находятся из решения системы алгебраических уравнений, составленной на основании первого закона Кирхгофа для производных от узловых токов.
Матрица инверсных индуктивностей, которая используется в системе линейных уравнений, симметрична относительно главной диагонали и элементы главной диагонали положительны. Поэтому предложено использовать метод квадратных корней, в котором требуется в два раза меньше операций по сравнению с методом Гаусса. Дифференциальные уравнения решаются методом Рунге-Кутта 4-го порядка, с шагом 0.001-0.0005 с. Выбранный метод при данном шаге имеет достаточные для расчетов электромеханических переходных процессов точность и время расчета.
Четвертый блок необходим для определения значений потокосцеплений и токов всех контуров в режимах коммутации ветвей. Расчет выполняется на основе обобщенного закона коммутации, согласно которому алгебраическая сумма потокосцеплений по любому замкнутому контуру до и после коммутации элемента остается неизменной. Потокосцепления находятся из решения преобразованных дифференциальных и алгебраических уравнений в третьем блоке.
По разработанной математической модели были рассчитаны режимы КЗ различной продолжительности для ТЭС с тремя агрегатами мощностью по 300 МВт каждый.
На рисунках 1 и 2 приведены графики зависимости тока статора генератора от времени при 3-фазных коротких замыканиях за блочным трансформатором на стороне 330 кВ. Как видно из графика на рисунке 1 при отключении короткого замыкания через 0.35 с после его возникновения, генератор еще сохраняет устойчивость. Неустойчивый режим работы генераторов возникает при отключении короткого замыкания на шинах высокого напряжения через время более 0.4 с после его возникновения. График тока статора генератора для этого режима показан на рисунке 2.

Рисунок 1–Изменение модуля тока статора генератора при 3-фазном КЗ на шинах ВН, при tкз равном 0.35 с
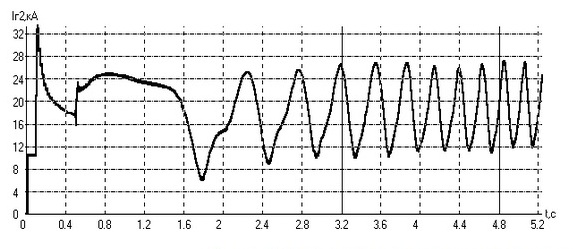
Рисунок 2–Изменение модуля тока статора генератора при 3-фазном КЗ на шинах ВН, при отключении короткого замыкания через 0.4 с
Характер изменения модуля тока статора при двухфазном коротком замыкании на землю на стороне ВН блока показан на рисунке 3. Продолжительность КЗ в данном опыте составляет 0.65 с.
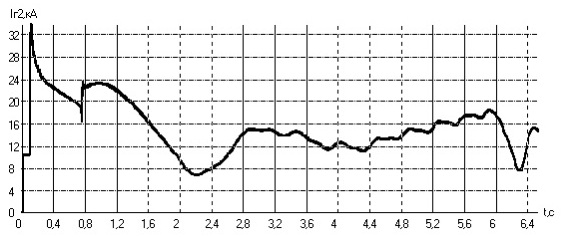
Рисунок 3–Изменение модуля тока статора генератора при 2-фазном КЗ на землю на шинах ВН, при tкз равном 0.65 с
Приведенные осциллограммы позволяют выполнить анализ поведения элементов электрической станции при КЗ и после их отключения устройствами релейной защиты. Например, при длительностях трехфазных КЗ менее 0.4 с динамическая устойчивость генераторов не нарушается. Предлагаемая модель позволяет более глубоко изучить процессы, происходящие в элементах электрической станции как в стационарных, так и в переходных режимах.
ЛИТЕРАТУРА
1.Сивокобыленко В.Ф., Меженкова М.А. Математическое моделирование электромеханических переходных процессов на электрических станциях. – Электрическтво, 2001, №4, С.5-9.