В настоящее время энергосистема Украины работает в таком режиме, когда в узлах нагрузки имеют место значительные отклонения напряжения и частоты от номинальных значений. Актуальным является определение в этих режимах потребляемой активной и реактивной мощностей асинхронной нагрузкой, являющейся преобладающей в узлах электрических систем. Этому вопросу посвящен ряд работ [1-3], однако в них рассматривается, как правило, отклонение только одного из влияющих параметров (напряжения или частоты), а также не учитывается влияние явлений вытеснения токов и насыщения магнитных цепей в асинхронных двигателях (АД) .
В данной работе с учетом указанных выше явлений в АД рассматривается влияние как каждого из режимных параметров (напряжения или частоты), так и их совместного воздействия. Типовая схема узла двигательной нагрузки приведена на рисунке 1. Составим математическую модель приведенной системы электроснабжения, в которой учтем соответствующими схемами замещения питающий трансформатор Т и асинхронные двигатели АД с учетом сопротивлений питающих кабелей. Здесь и далее все параметры схем замещения будем приводить в относительных номинальных единицах.
Особенностью использованных в данной работе схем замещения АД (рис. 2) является то, что в них учтены потери в меди статора и ротора, явления вытеснения тока в роторе и насыщения магнитных путей по цепи главного магнитного потока и потоков рассеяния. С учетом этих явлений разработана методика получения указанных на рисунке 2 параметров по исходным каталожным данным, типовой характеристике холостого хода АД и принятой по [4] зависимости потерь в стали от явления гистерезиса ивихревых токов. Последняя учитывается путем представления активного сопротивления ветви намагничивания в виде двух составляющих, одна из которых отражает гистерезисные потери, пропорциональные первой степени частоты напряжения, а вторая – потери от вихревых токов, пропорциональные квадрату частоты, т. е.

где n - отношение текущей частоты w к номинальной.
Ток намагничивания АД нелинейно зависит от напряжения, что можно учесть с помощью типовой характеристики холостого хода. Тогда с учетом (1) сопротивление ветви намагничивания Zm можно представить функцией
Индуктивные сопротивления рассеяния обмоток АД нелинейно зависят от соответствующих токов. Эту зависимость учтем в сопротивлении статорной цепи, как:
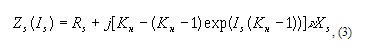
где Kн – коэффициент насыщения по потокам рассеяния, принимаемый равным 0,6 – 0,95.
Входное сопротивление двигателя, ток статора, активную и реактивную потребляемые мощности находим по соотношениям:
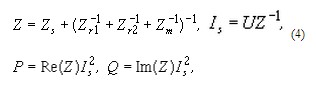
здесь скольжение s, необходимое для определения сопротивлений контуров ротора, находится из решения нелинейного уравнения, отражающего равенство вращающего момента АД, являющегося функцией напряжения, частоты и скольжения, а также момента сопротивления АД, зависящего от коэффициента загрузки Кз и скорости вращения.
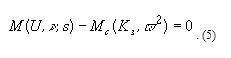
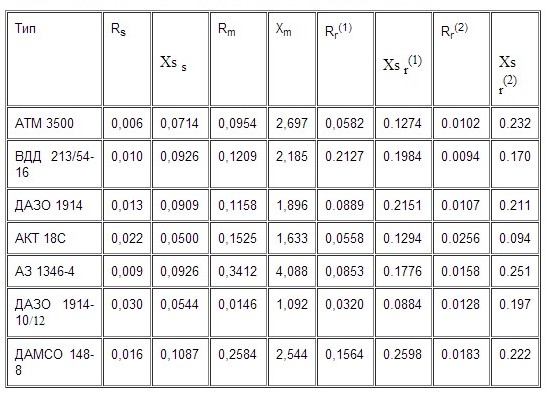
В качестве примера по указанной методике были определены параметры схем замещения двигателей 6 кВ, используемых в системах электроснабжения собственных нужд блочных электростанций с агрегатами 200 и 300 МВт, которые представляют собой узлы асинхронной нагрузки. Каталожные данные АД такого узла нагрузки для блока 200 МВт приведены в таблице 1, а параметры их эквивалентных схем замещения – в таблице 2. Питающий трансформатор принят типа ТРДН-32000/220/6,3/6,3 мощностью 32 МВА. В таблице 1 указаны также значения коэффициентов загрузки механизмов, которые имееют место при работе блока с номинальной нагрузкой. Эти же значения принимались при расчетах на ПЭВМ. Параметры схем замещения АД (табл. 2) приведены для статора, ветви намагничивания и двух контуров ротора, эквивалентно заменяющих глубокий паз. Значение активного и индуктивного сопротивлений ветви намагничивания указаны для номинального режима, когда напряжение и ток статора, а также скольжение АД равны номинальным значениям. Рассчитанные по указанным параметрам схем замещения режимы работы АД для номинального и пускового режимов в точности соответствуют приведенным паспортным данным АД (табл. 1).
Таблица 1–Паспортные данные АД напряжением 6 кВ
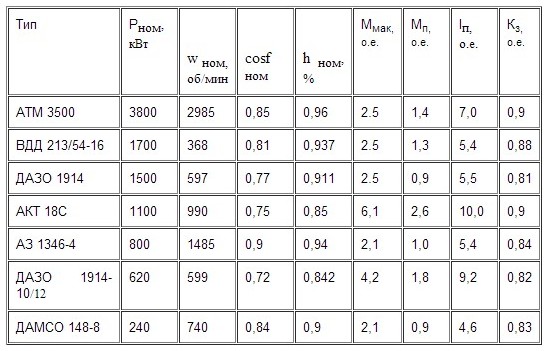
Таблица 2–Параметры эквивалентных схем замещения АД напряжением 6 кВ
Используя указанные параметры схем замещения АД, уделим основное внимание зависимостям от напряжения и частоты активных и реактивных мощностей, потребляемых узлом с двигательной нагрузкой
Так как в схему замещения АД входят сопротивления, нелинейно зависящие от напряжения и частоты питания, а также от соответствующих токов, то для получения решения используется метод итераций. Момент сопротивления нагрузки на валу двигателя может быть учтен с помощью полиномов второй или третьей степени от скорости вращения или же как постоянный. Примеры полученных решений для одного двигателя содержатся в [5].
Для узла нагрузки (рис. 1) можно определить активную (P) и реактивную (Q) мощности, как сумму мощностей отдельных двигателей и потерь в трансформаторе:
При неизменной частоте питающего напряжения и заданных коэффициентах загрузки двигателей (табл. 1) характер изменения P и Q от напряжения питающей системы показан на рисунке 3. Как видно из приведенных данных, при понижении напряжения значительно (близко к квадратичной) снижаются полная и реактивная мощности узла, тогда как активная снижается весьма незначительно. Ток статора секции при этом возрастает и в зависимости от загрузки может превысить номинальный ток трансформатора.
Аналогичные зависимости P и Q от частоты питающего напряжения при неизменной величине последнего (U=Uном) и тех же условиях по загрузке двигателей приведены на рисунке 4. Активная мощность узла нагрузки практически прямо пропорциональна частоте. Это связано с тем, что момент сопротивления на валу АД зависит от частоты вращения ротора. Таким образом при понижении частоты производительность механизмов с.н. снижается, что может вызвать снижение мощности выдаваемой блоком в энергосистему и усугубить дальнейшее неблагоприятное развитие создавшегося аварийного режима. Полная и реактивная мощности при снижениях частоты сначала убывают, а затем возрастают, т. е. имеют минимумы при определенных значениях частоты. Такой же характер зависимости имеет и ток статора.
При одновременном изменении величины и частоты питающего напржени по известному закону регулировани зависимости P и Q, при заданных Kz с зависимыми от скорости вращени моментами сопротивленими АД, показаны на рисунке 5, а при при независимых от скорости вращени моментах сопротивлени – на рисунке 6. В первом случае имеет место тенденци к уменьшению всех мощностей при понижених частоты. Ток статора при этом изменетс незначительно. Во втором случае мало изменютс все потреблемые мощности, а ток статора возрастает обратно пропорционально частоте. Таким образом, двигателии трансформатор будут испытывать перегрузку в подобного типа режимах. Математическа модель позволет исследовать и другие законы совместного изменени частоты и напржени и оределить наиболее благопритный из них для узлов асинхронной нагрузки.
ЛИТЕРАТУРА
1. Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей./ Под ред. Мамиконянца Л.Г. Энергоатомиздат, М. 1984. – 240 с.
2. Копылов И.П. Электрические машины: Учебник для вузов. – М.: Энергоатомиздат, 1986. – 360 с.
3. Электрическая часть станций и подстанций. Ч. 2. Под ред. А. А. Васильева. М. Энергия, 1972. – 344 с.
4. Сандлер А.С., Сарбатов Р.С. Автоматическое частотное управление асинхронными двигателями. М., Энергия, 1974. – 328 с.
5. Талал Ал Ас, Математическое моделирование процессов в системе электроснабжения собственных нужд электростанций при отклонениях напряжения и частоты/ Сб. науч. тр. ДонГТУ. Серия “Электротехника и энергетика”. – Вып.17. – Донецк, ДонГТУ, 2000. – c. 184 – 189