Аннотация
The aim of this paper is to study possible effect of changing “slow” oxygen content on electrophysical properties of HTSC cuprates. Magnetization of Sm-doped samples YBa1.90Sm0.10Cu3Ox was measured in a vibrating sample magnetometer in scanning magnetic field and temperature. The study of magnetic hysteresis in these samples shows that additional oxidation with respect to “slow” component produces HTSC with higher both the critical temperature Tc and intragrain critical current density Jcg in ceramic specimens. in untextured ceramic specimens was observed.
Introduction
A characteristic feature of high-temperature superconducting (HTSC) cuprates is a strong dependence of their structural and electrophysical properties on oxygen nonstoichiometry. Cuprates exhibit large oxygen nonstoichiometry: depending on temperature and oxygen partial pressure in the ambient, oxygen index x in barium-yttrium cuprate YBa2Cu3Ox (YBCO) changes in the interval 6.2 < x < 7.0 at equilibrium and in metastable state – from 6.0 to 7.0 [1, 2]. Oxygen in YBCO exists in two forms: strongly and weakly bound. The strongly bound oxygen is in the state of oxidation -2 (usual for oxides) and its amount is constant: 6.0 mole O per formula unit. The weakly bound oxygen is evolved when cuprate is dissolved in acids and its oxidation number exceeds -2 (which is met, e. g., in peroxides). This form of oxygen is completely responsible for oxygen nonstoichiometry and its amount δ is a variable part of general oxygen content: x = 6 + δ [1, 2].
Earlier we found that in barium-yttrium cuprate YBa2-yREyCu3Ox doped with a rear-earth (RE) element a new, additional constituent (γ) of oxygen nonstoichiometry is realized so that x = 6 + δ + γ [3, 4]. Contrary to usually observed nonstoichiometric oxygen (δ), this additional part of nonstoichiometry shows a very slow kinetics of relaxation and also gives the possibility of oxygen content higher than 7 mole per formula unit: x > 7,0. According to these data, we need to distinguish two unlike components of weakly bound oxygen in nonstoichiometric cuprates: usual “quick” δ and additional “slow” γ. Slow oxygen appears in cuprates doped with heterovalent substitutes such as RE at Ba sites.
In air ambient, the highest content of “slow” oxygen may be obtained after keeping a sample to equilibrium below Tb1 = 740 °C and this extra oxygen content equals to RE amount: γmax = y. This implies the following scheme of Ba substitution for RE: [SmBa•] = [Ob’]. Above Tb2 = 840 °C, “slow” oxygen is completely lost from the sample, γmin = 0 [3, 4].
The aim of this paper is to study possible effect of changing “slow” oxygen content on electrophysical properties of HTSC cuprates. Magnetization of Sm-doped samples YBa1.90Sm0.10Cu3Ox was measured in a vibrating sample magnetometer in scanning magnetic field and temperature.
Preparation of nonstoichiometric samples
Cuprate samples doped with Sm according to the formula YBa2-ySmyCu3Ox (y = 0 – 0,10 with the step 0,02) were studied. Although the batch formula suggests introduction of Sm instead Ba, ionic radii considerations (r(Y) = 1.02 Å, r(Sm) = 1.079 Å, r(Ba) = 1.42 Å ), show that a change in stoichiometric ratio of large (as compared to Cu) cations at Y and Ba sites is expected: (Y+Sm)/Ba = (1+y)/(2–y).
The samples were synthesized through a standard ceramic procedure. As starting reagents Y2O3 (“ITO-LUM”), CuO (“pure for analysis”), BaCO3 (“highly pure 9–3”), and Sm2O3 (“highly pure”) were used. We focused on attaining homogeneous single-phased state of synthesized samples. Weighed portions of starting reagents were ground and mixed in an agate mortar under layer of ethanol. Mixed and ground powders were pressed into pellets and fired in air at 880–930 °С for 30–40 hours. To improve the links between the grains of reacting substances, intermediate grindings of reaction mixtures were performed after each 6–8 hours during solid-state synthesis. The pattern of X-ray diffraction in Fig. 1 (a DRON-3 diffractometer, Cu Kα radiation) confirms completion of synthesis, single-phase state and good crystallinity of powder sample after firing at 920 °C for 40 h. Finally, the samples of synthesized powders were formed into plates with dimensions 15 x 5 x 1 mm and sintered at 930–940 °C for 2–3 hours with the following slow cooling (<100 °C/h) to room temperature.
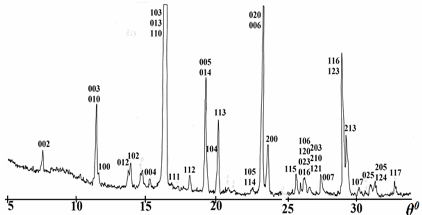
Fig. 1 – X-ray powder diffraction pattern from single-phased YBa1.90Sm0.10Cu3Ox after synthesis at 920 °С for 40 h.
The SEM microphotograph (JSM-35C, JEOL) taken from sintered sample (Fig. 2) shows well formed crystalline grains, often platelike, with quite clear surfaces. They are distributed in sizes from 5 to 20 µm.

Fig. 2 – SEM microphotograph of sintered sample YBa1.90Sm0.10Cu3Ox White segment = 10 µm.
A series of electron probe local analyses taken from different grains of the sample (Fig. 3) shows the presence of only one phase – 123 cuprate. Assessment of the joint data of electron microscopy, X-ray diffraction and local electron probe analyses comes to unambigious conclusion that the sample presents a single-phased homogeneous 123 cuprate without any foreign phase inclusions.

Fig. 3 – A typical energy-dispersive spectrum of electron probe local analysis of sintered sample YBa1.90Sm0.10Cu3Ox.
Two series of samples YBa1.90Sm0.10Cu3O6+δ+γ were prepared for measurements: with maxim (I) and minimum (II) values of “slow” oxygen content: γ(I) = 0.10 and γ(II) = 0.00 respectfully. Both types of samples were obtained from the same batch of sintered material. Samples (I) were brought to equilibrium at 720 °C (lower than Tb1) to maximize the “slow” oxygen content: γmax = 0.10. Then they were cooled to 400 °C and kept at this temperature for 1 h to maximize “quick” oxygen content. The final total oxygen content in the samples of this series was established at x (I) = 7.07 (YBa1.90Sm0.10Cu3O7.07).
Samples (II) were brought to equilibrium at 900 °C (above Tb2) to minimize the “slow” oxygen content: γmin = 0.00 and then they were rapidly (in less then 10 min) cooled to and kept at 400 °C for 1 h. The final total oxygen content in the samples of this series was equal to x (II) = 6.97 (YBa1.90Sm0.10Cu3O6.97).
Results of magnetic measurements
Magnetic moments of samples were measured by a Foner’s vibrating sample magnetometer (VSM). The measurements were conducted in scanning magnetic field (reversal field Hmax = 8 kOe) and temperature (reversal point above Tc) modes.
In Fig. 4 temperature dependences of magnetization M of the samples I and II in heating-cooling cycles are compared. These measurements were performed in a low external field (H ≈ 2 Oe) and with the reversal temperature well above the critical temperature Tc. A typical time period taken for measurements in a heating-cooling cycle starting and ending at about 5 K was half an hour.


Fig. 4 – Hysteresis of magnetization at thermocycling samples (I) – (a) and (II) – (b).
Observed hysteresis is typical for type-II superconductors. Two branches of the hysteresis curve meet at the point that corresponds to the critical temperature Tc. At Tc a negative diamagnetic moment of a superconducting sample disappears. In Fig. 4 these points are indicated with vertical dashed lines.
As obtained from the data in Fig. 4, the critical temperature of sample I (YBa1.90Sm0.10Cu3O7.07) is Tc(I) = 93.4 K as compared to Tc(II) = 91.7 K for sample II (YBa1.90Sm0.10Cu3O6.97). Thus, maximizing “slow" oxygen content (γmax = 0.10) may somewhat increase Tc.
Figure 5 demonstrates magnetic hysteresis loops taken from sample I (YBa1.90Sm0.10Cu3O7.07) at different temperatures, in this case at 5 and 75 K.

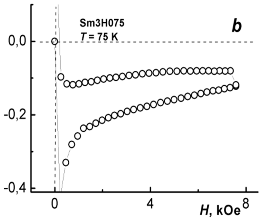
Fig. 5 – A loop and a half-loop of magnetic hysteresis in YBa1,90Sm0,10Cu3O7.07 at 5 K (a) and 75 К (b).
It is well known that type-II superconductors exhibit magnetic hysteresis. Finite resistivity and magnetic hysteresis in these superconductors appear because the motion of flux filaments is pinned by defects such as voids, inclusions, dislocations, grain boundaries, and compositional variations. This pinning results in an irreversibility of metastable states, which manifest themselves in hysteresis. In HTSC ceramics, important factor is the sensitivity of critical current of weak links to local intergrain fields [5]. When the flux filaments depin by thermal activation, or because a current density exceeds some critical value, their motion induces an electric field [6].
The difference between the values of magnetization M (specific moment m) on ascending (Masc) and descending (Mdes) branches of the hysteresis loop (ΔM = Masc – Mdes) at a given strength of magnetic field may serve as a measure of pinning efficiency in type-II superconductor and thus assess its practical effectiveness. The critical current density Jc may be estimated in frames of Bean model [7], which assumes that the critical current density does not depend on magnetic field (Jc(H) = const). The value of Jc may be obtained from the following formula:
Jc = 15 (ΔM/R), A/cm2,
where ΔM is the width of the magnetization hysteresis loop (ΔM = Masc – Mdes) in emu/cm3; R is the radius of the sample, cm.
In strong magnetic fields this formula may be used for estimation of the value of intragrain critical current density Jcg (the current flowing inside the grains [5]) in ceramic samples. In this case R is the radius of a single grain.
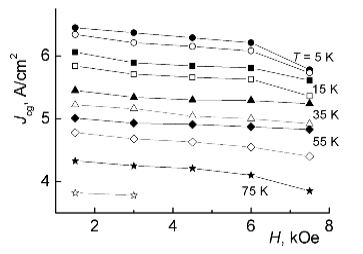
Fig. 6 – Intragrain critical current densities Jcg in samples I (black symbols) and II (open symbols) under different fields H and temperatures T.
It is interesting to compare samples I and II from this point of view. In Fig. 6, the calculated values of Jcg (in logarithmic scale) are plotted against magnetic field H at different temperatures both for sample I and II. From this comparison, the advantage of HTSC samples fully oxidized with respect to “slow” component of oxygen nonstoichiometry is evident (Fig. 6). Under all fields and temperatures, the critical current densities in sample I are greater approximately by factor of 2 or more than those in sample II. In sample I the density of critical current at 5 K in lower magnetic fields is Jcg ≈ 3·106 A/cm2.
Conclusion
Excess oxidation found in cuprates with cation nonstoichiometry due to heterovalent doping may be of practical interest due to somewhat higher both the critical temperature Tc and intragrain critical current density Jcg in ceramic specimens.
References
- Приседский В. В., Ройзенблат Е. М., Удодов И. А., Гусакова Л. Г., Климов В. В. Ро2 – Т фазовая диаграмма купрата бария-иттрия YBa2Cu3О9-у // Доклады АН УССР. – 1988. – № 3. – С. 59–62.
- Приседский В. В., Михеенко П. Н., Иванченко Ю. М., Сухаревский Б. Я., Шаталова Г. Е., Гусакова Л. Г., Малышев Е. Н., Ройзенблат Е. М., Сухорукова И. Э., Удодов И. А., Климов В. В. Слабосвязанный кислород и сверхпроводимость в YBa2Cu3Оx // Физ. низких температур. – 1989. – Т. 15. – № 1. – С. 8.
- Н. В. Маркова, В. В. Приседский Слабо связанный кислород в купрате бария-иттрия, нестехиометричном по катионам и легированном Sm, Nd, и Gd // Наукові праці Донецького національного технічного університету. Серія: Хімія і хімічна технологія. – 2012. – Вип. 18 (198). – С. 28–35.
- В. В. Приседський, Н. В. Маркова, І. О. Удодов, О. І. Волкова Два типи слабко зв’язаного кисню в купраті барію-ітрію, легованому самарієм // Вопросы химии и химической технологии. – 2011. № 5 – С. 396–401.
- A. I. D’yachenko, V. V. Chabanenko Irreversible phenomena in the absorption of electromagnetic field in HTSC plates // Fiz. Nizk. Temp. – 1992. – V. 18, No. 8. – P. 826–837.
- L. Mayergoyz Superconducting Hysteresis. In: G.Bertotti, L.Mayergoyz (editors) The Science of Hysteresis. Elsevier. – 2005. – P. 257–335.
- C. P. Bean Magnetization of hard superconductors // Phys. Rev. Lett. – 1962. – V. 8. – P. 250–252.