Аннотация
Усталостное разрушение рассматривается как двухстадийный процесс, включающий наработку до момента зарождения поверхностного дефекта и стадию докритического развития магистральной трещины. Учёт стадии живучести открывает возможность решения ряда важных практических задач, в частности: определение допустимых границ развития дефекта, установление периодичности контроля, оценка остаточного ресурса, аргументированное повышение нормативных сроков эксплуатации и др.
Проблема обеспечения надежности машиностроительных конструкций во многом обусловлена ограниченностью ресурса ответственных деталей, испытывающих в процессе работы интенсивное повторно-переменное нагружение. В применяемых в настоящее время инженерных методах расчета ресурс деталей оценивается коэффициентом запаса по долговечности, который вычисляется с применением средних значений нагрузок и характеристик усталостной прочности материала. При этом в качестве критерия разрушения принимается наработка, соответствующая моменту зарождения усталостной микротрещины.
Вместе с тем практика показывает, что в ряде случаев целесообразным является продолжение эксплуатации конструкции в обычном режиме при наличии стабильно и контролируемо развивающихся в них усталостных трещин. Учет стадии живучести позволяет на этапе проектирования обоснованно определять допустимые границы развития дефектов, устанавливать периодичность контрольных мероприятий и аргументированно повышать нормативные сроки эксплуатации изделий.
Настоящая работа демонстрирует возможность прогнозирования процесса формирования отказов по критерию усталостного разрушения путем последовательного описания стадий зарождения и докритического развития трещин.
Рассматривается задача прогнозирования надежности гусениц быстроходных транспортных машин. Траки гусеницы имеют сложную конфигурацию в виде системы тонкостенных элементов с нерегулярным оребрением. В условиях эксплуатации быстроходных машин траки гусениц испытывают случайное внешнее воздействие со стороны грунта и сопряженных деталей: опорных катков, ведущего и направляющего колес.
На рис. 1 представлен фрагмент типичной осциллограммы процессов изменения напряжений в опасных зонах траков, полученной путем тензометрирования в условиях реальной эксплуатации машины.
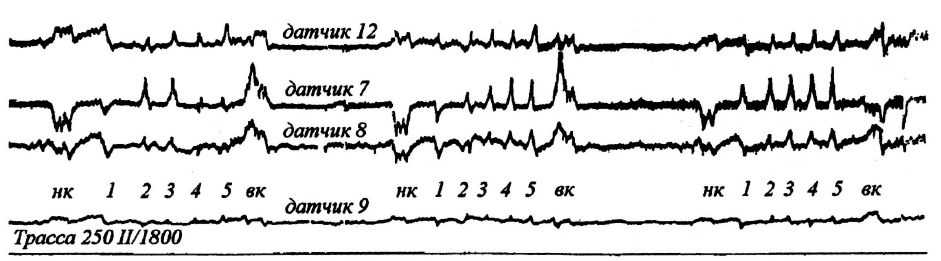
Рис. 1. Фрагмент характерных осциллограмм процессов изменения напряжений в зонах образования усталостных трещин
При статистической обработке осциллограмм была выполнена схематизация процессов по методу случайных импульсных потоков и получены законы распределения напряжений, соответствующие различным сочетаниям природно-климатических условий и режимов эксплуатации гусеничных машин. На рис. 2 в качестве иллюстрации показаны плотности распределений приведенных к симметричному циклу амплитуд напряжений в опасных зонах. Закон распределения напряжений для обобщенных условий эксплуатации в заданном регионе определяется выражением
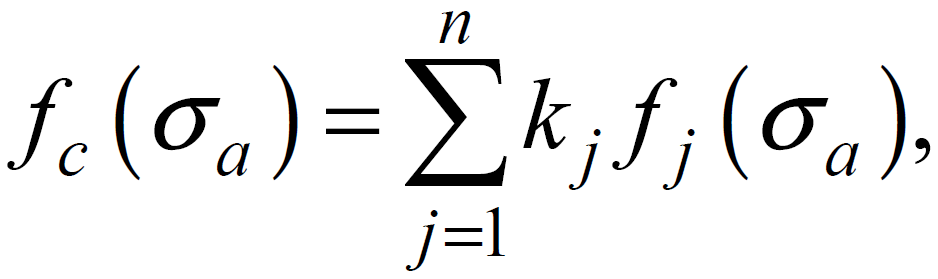
где n - число сочетаний условий и режимов эксплуатации; к - весовые коэффициенты.

Рис. 2. Плотности распределений амплитуд напряжений: 1 - летняя проселочная дорога; 2 - зимняя проселочная дорога; 3 - зимняя проселочная дорога, бесснежная, мерзлый грунт
Усталостное разрушение рассматривается как двухстадийный процесс формирования отказа. На стадии зарождения трещин расчет долговечности выполняется по общепринятой методике [1], базирующейся на корректированной гипотезе линейного суммирования повреждений и предположении о логарифмически нормальном законе распределения наработки. Математическое ожидание и среднеквадратическое отклонение логарифма долговечности определяются выражениями:

где L - долговечность траков до момента зарождения усталостных трещин, выраженная в километрах пробега; N0, m, М[σ-1д], σ [σ-1д] - параметры вероятностной диаграммы выносливости детали; ар - коэффициент корректировки гипотезы линейного суммирования повреждений; vi , σа1 - параметры блока случайного нагружения.

Рис. 3. Функция надежности траков гусеницы: 1 - функция надежности по критерию зарождения усталостной трещины; 2 - функция надежности по критерию хрупкого разрушения
Необходимые для расчета характеристики выносливости были определены путем усталостных испытаний представительных партий натурных деталей при различных уровнях напряжений. Статистической обработкой результатов получены следующие значения параметров вероятностной диаграммы: математическое ожидание и среднеквадратическое отклонение предела выносливости на базе N0 = 107 циклов, а также показатель, определяющий наклон квантильных кривых выносливости, соответственно равны
М [σ-1д] = 115 МПа,
σ[σ--1д] = 20,5 МПа, m = 6,1. На рис. 3 (кривая 1) приведена функция вероятностей безотказной работы (функция надежности) траков по критерию зарождения усталостной трещины, соответствующая одному из наиболее тяжелых условий эксплуатации гусеничных машин на дорогах с жестким покрытием (кривая 3 на рис. 2). Расчет показывает, что гамма-процентный ресурс траков Lγ=0,9 в этих условиях составляет 2000 км пробега.
Этот результат вполне удовлетворительно согласуется с данными контрольных осмотров.
Вторая стадия усталостного разрушения представляет процесс стабильного развития одной (реже нескольких) из ранее образовавшихся микротрещин. Работоспособность конструкции при этом сохраняется, она будет исчерпана лишь при достижении критического сочетания длины трещины и уровня нагрузки, когда стабильный рост трещины сменяется лавинообразным. Для анализа кинетики развития усталостной трещины используют обычно силовой подход механики разрушения, в соответствии с которым скорость роста трещины в цикле определяется, например, формулой Пэриса
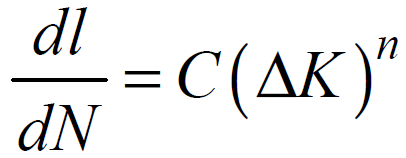
(ΔК - размах коэффициента интенсивности напряжений (КИН) в цикле; С, n - константы материала в данных условиях).
Отличаясь простотой, данное соотношение не отражает, например, влияния среднего напряжения цикла, в связи с чем его идентификация должна производиться в условиях, соответствующих эксплуатационным.
Как показал анализ, для определения КИН в траке не могут быть непосредственно использованы приводимые в справочной литературе (например, [2]) аналитические выражения: рассматриваемый объект значительно сложнее. Самостоятельное же решение этой задачи с использованием, например, функции комплексной переменной затруднительно даже с учетом упрощения расчетной схемы (рис. 4). Таким образом, наиболее приемлемым оказался численный метод - метод конечных элементов расчета КИН в терминах энергетического подхода.

Рис. 4. Элемент конструкции с трещиной в ребре
В соответствии со сказанным трак с учетом симметрии дискретизировали трехмерной сеткой конечных элементов, сгущенной в зоне возникновения и роста трещин в ребре и в окрестности вершины трещины. Для ряда длин трещины при единичной нагрузке подсчитывали интенсивность выделения упругой энергии
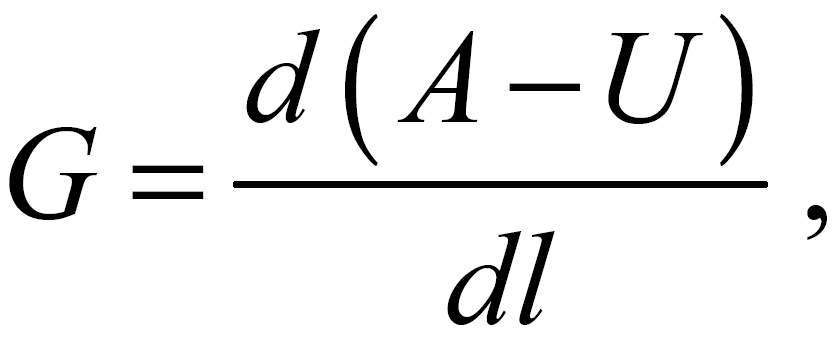
где А - работа внешней нагрузки; U - потенциальная энергия, связанная с упругой составляющей деформации. С использованием однозначной в рамках линейной механики разрушения связи между параметрами G и К определяли зависимость КI(l) в виде
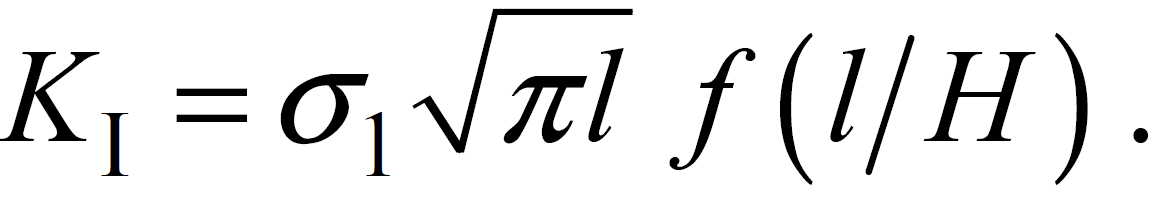
Здесь σ1 - номинальное напряжение от единичной нагрузки; l - длина трещины в ребре; f (l/H) - поправочная функция, определяемая относительной длиной трещины; H - высота ребра.
Условие разрушения имеет традиционный вид
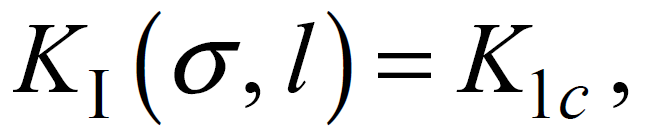
где К1 (σ, l) - текущее значение КИН; σ = рσ1 - номинальное напряжение от действующей нагрузки (р - параметр нагрузки); К1с - предел трещиностойкости, представляющий характеристику сопротивления росту трещин в конструкции из данного материала.
Определение параметров уравнения Пэриса и характеристики трещиностойкости траков из стали Г13ЛА было выполнено по данным усталостных испытаний представительных партий натурных деталей. В ходе испытаний варьировали уровень амплитуды номинальных напряжений; в процессе наработки регистрировалась также длина развивающихся трещин. На рис. 5 в качестве иллюстрации показаны отдельные результаты исследования.

Рис. 5. Кинетика развития усталостных трещин в траке (по данным испытаний)
Соответствующей статистической обработкой экспериментальных данных идентифицированы коэффициенты уравнения Пэриса и значения предела трещиностойкости К1с. Установлено, что рассеяние коэффициентов можно описать нормальным законом с параметрами:

Зависимость предела трещиностойкости, ставящая в соответствие длине трещины предельное в данных условиях значение коэффициента интенсивности напряжений, представлена на рис. 6.
Расчет долговечности траков по критерию хрупкого разрушения сводится к решению связанной нелинейной задачи, в которой необходимо учесть случайный характер нагружения и рассеяние характеристик, определяющих рост трещин (С, n) , а также предела трещиностой-кости.
Для реализации этой задачи применен численный метод Монте-Карло. Генераторами случайных чисел каждой детали из представительной выборки присваиваются случайные значения начальной длины трещины, параметров кинетического уравнения (формулы Пэриса) и характеристики трещиностойкости. Случайное нагружение моделирует один из генераторов, воспроизводящий закон распределения амплитуд напряжений. Выполняется пошаговый расчет отдельных деталей, при котором в каждом шаге нагружения вычисляются текущее значение коэффициента интенсивности напряжений Кь его размах, а затем приращение усталостной трещины и ее длина. По характеристике трещиностойкости с учетом рассеяния определяется величина критического значения коэффициента интенсивности напряжений К1с. Если для рассматриваемого нагружения данной детали выполняется условие
КI < К1с (l),
то производится следующий цикл пошагового расчета, иначе
КI ≥ К1с (l),
полученная для этой детали в данном шаге длина трещины признается критической, а соответствующий номер цикла определяет долговечность объекта. Описанная процедура воспроизводится для каждой детали выборки. Получаемые при этом значения долговечности образуют выборку случайной наработки до отказа, статистической обработкой которой могут быть получены функция повреждаемости и функция вероятностей безотказной работы гусеницы на стадии живучести. На рис. 3 функция надежности по критерию зарождения трещин (кривая 1) дополнена функцией надежности по критерию хрупкого разрушения (кривая 2). Напомним, что приведенные результаты соответствуют наиболее тяжелым условиям эксплуатации гусеничных машин. Из их сопоставления следует, что даже в этих условиях обоснованный переход к эксплуатации по нормам, допускающим контролируемый процесс стабильного развития усталостных трещин в траках, позволяет примерно в полтора раза увеличить продолжительность эксплуатации гусениц.

Рис. 6. Экспериментальные данные и аппроксимация зависимости предела трещиностойкости от длины трещины
Отметим в заключение, что представление результатов расчета в виде функций вероятностей безотказной работы позволяет расширить круг практических задач надежности, решаемых на этапах проектирования и эксплуатации, в частности:
- значительное увеличение срока службы изделий за счет обоснованного перехода от предельного состояния по критерию зарождения усталостных трещин к предельному состоянию по критерию начала неустойчивого их развития;
- возможность оценки остаточного ресурса ответственных деталей по данным контрольных осмотров и назначение продолжительности межосмотровых интервалов;
- обоснование периодичности контрольных мероприятий;
- рациональный выбор материала на основе сравнительной оценки характеристик усталостной прочности и трещиностойкости;
- разработка методов и средств технической диагностики.
Литература
- Когаев, В.П. Расчеты на прочность при напряжениях, переменных во времени / В.П. Когаев. - М.: Машиностроение, 1993. - 364 с.
- Справочник по коэффициентам интенсивности напряжений: в 2 т. / Ю. Ито, Ю. Мураками, Н. Хасебэ и др.; ред.: Р.В. Гольдштейн, Н.А. Махутов. - М.: Мир, 1990. - Т. 1. - 448 с.; Т. 2. -560 с.