Авторы:Воробьев Ю.С., Чернобрывко М.В.
В статье рассмотрены способы подготовки поверхностей деталей для напыления газотермических покрытий, для повышения качественных свойств.
Источник:Сборники научных работ НТУ ХПИ, научно-техничнический журнал "Механика и Машиностроение"
При исследовании прочности плит значительный интерес представляет анализ напряженного состояния при воздействии ударно-волновой нагрузки [1]. Такие задачи возникают при анализе прочностной надежности морских платформ и прибрежных защитных сооружений, которые подвергаются воздействиям как гидродинамического, так и ударно-волнового характера.
Исследовалось два варианта нагружения: воздействие ударной волны избыточного давления в воздушной среде и воздействие гидродинамической нагрузки. В обоих случаях рассматривалась плита длиной 10 м, шириной 3 м и толщиной 0,5 м. Материал плиты характеризуется следующими свойствами: ρ=2400 кг/м3,ν=0,3, Е=104 МПа.
Предварительная обработка поверхности основы является одним из основных факторов обеспечивающих высокую прочность сцепления покрытия с основой, т.к. в большинстве случаев соединение напыленного покрытия с материалом детали проиcходит в результате механического сцепления. Следовательно, для того, чтобы напыляемые частицы, которые ударяются и деформируются об основу, прочно сцеплялись с напыляемой поверхностью, основа должна иметь оптимальную шероховатость.
Как правило, поставленная задача в общем виде решается на основе вариационных методов исследования с использованием метода конечных элементов [2]. Однако, при исследовании конкретных задач особо важно учитывать неравномерность распределения нагрузки как по поверхности плиты, так и во времени. При этом деформационные процессы в плите неоднородны. Зоны упруго-пастических деформаций локализованы, и их границы изменяются во времени.
Решение задачи проводится на основе метода конечных разностей [3] с использованием вложенной прямоугольной сетки [4]. Такой подход позволяет снизить погрешность при линеаризации задачи в локальных зонах упругопластического деформирования [5]. В качестве критерия контроля погрешности по шагу во времени выбираем локальную погрешность решения:
где U – точное, а u – приближенное решения для выбранного момента времени tk+1, при условии, что для предыдущего момента времени tk эти решения совпадают. При этом получаем для фиксированного tk+1 массив локальных погрешностей et,h. Контроль величин et,h позволяет путем половинного деления конечно-разностной сетки определять величины et/2,h и et,h/2, и тем самым корректировать максимальную погрешность вычислений, согласно (1).
Реакция плиты на импульсную нагрузку исследовалась на основе численного эксперимента [6] воздействия фронта ударной волны на плиту. В результате расчетов определялась поверхность избыточного давления, которое воздействует на конструкцию в заданный интервал времени. Дальнейшая обработка результатов позволяет построить поверхность максимальных значений избыточного давления для всей плоскости ху исследуемой плиты (рис. 1).
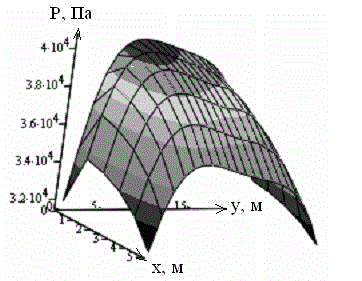
Рисунок 1 – Поверхность избыточного давления
Анализ поверхности, построенной по максимальным значениям избыточного давления на каждую исходную ячейку исследуемой конструкции, позволяет сделать вывод о достаточной гладкости функции Р(y, x). В силу этого, для дальнейшего исследования в задаче о прочности и целостности элементов строительного сооружения при ударно-волновом воздействии достаточно определить максимальный элемент поверхности и координаты ячейки приложения этой величины.
Рассматривался случай, когда численное значение максимальной нагрузки соответствовало величине 0,4 атмосферы или 0,4x101325=40530 Па. Максимальная нагрузка достигалась в точке с координатами (y, x)=(0.25 м, 0.82 м). Рассматривались перемещение (рис. 2) и интенсивность напряжений (рис. 3) в заданной точке.
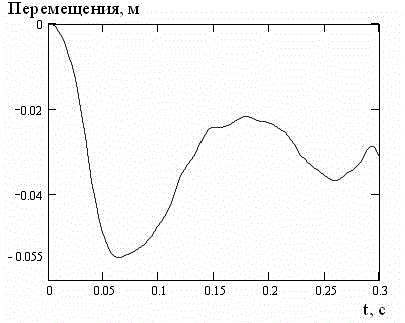
Рисунок 2 – Перемещения при импульсном нагружении
Анализ рис. 2 и 3 позволяет сделать вывод о затухании волнового процесса в плите с течением времени. Однако, максимальная величина интенсивности напряжения, равная 181 МПа, свидетельствует о большой вероятности разрушения конструкции в искомой точке, что может повлиять на целостность плиты вцелом.
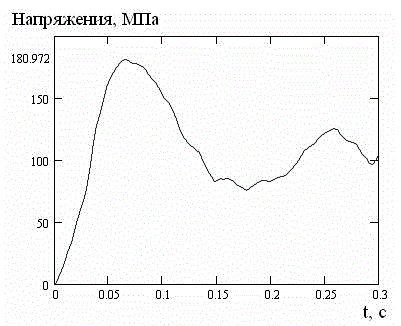
Рисунок 3 – Интенсивность напряжений при импульсном нагружении
При исследовании воздействия гидродинамической нагрузки на плиту в качестве нагрузки выбирались экспериментальные данные по накату уединенной волны на вертикальную стенку. В качестве вертикальной стены рассматривалась описанная выше плита. Результаты эксперимента были получены в рамках данного проекта в работах Института гидродинамики им. М.А. Лаврентьева СО РАН (ИГиЛ), Института вычислительной техники СО РАН (ИВТ) и Кемеровского государственного университета(КемГУ) [7].
На рис. 4 представлены результаты для гидродинамической нагрузки F/(rgh2), действующей на вертикальную стенку, и значения безразмерного гидродинамического давления P/(rgh) в угловой точке, где ρ – плотность жидкости, h – глубина жидкости вдали от волны, g – ускорение свободного падения. Уединенная волна с начальной амплитудой a/h=0,5 набегает на вертикальную стенку, которая располагалась на расстоянии x/h=15 от начального положения вершины волны. Отметим, что во все моменты времени максимальное значение давления на вертикальной стенке достигается в угловой точке. Кривым 1 и 2 показаны результаты, полученные в ИГиЛ, кривыми 3 и 4 – в КемГУ, кривая 5 показывает распределение гидродинамического давления, полученного в ИВТ (значения для давления в угловой точке не определялись).
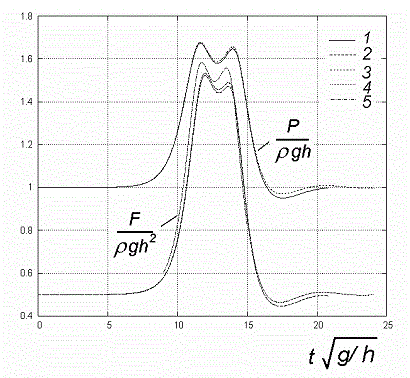
Рисунок 4 – Гидродинамические нагрузки на плиту
Видно, что имеется достаточно хорошее согласие с численными расчетами, выполненными в ИГиЛ СО РАН и КемГУ, как для гидродинамической силы, так и для давления в угловой точке. Значения для гидродинамической силы, полученные в ИВТ СО РАН, несколько отличаются, что может быть связано с погрешностями счета.
Анализ результатов, представленных на рис. 4 позволил определить максимальное расчетное значение гидродинамической нагрузки, зависящее от глубины слоя жидкости. Величина Р=16 667h Па использовалась для прочностных расчетов определения напряженно-деформированного состояния плиты. Исследовались перемещения и интенсивности напряжений для плит при h=1 м, h=2 м и h=3 м. Сравнивались максимальные величины.
На рис. 5 и 6 представлены перемещения и интенсивности напряжений для глубины h=1 м.
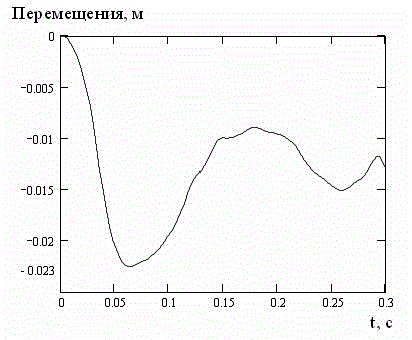
Рисунок 5 – Перемещения при гидродинамической нагрузке для глубины h=1 м
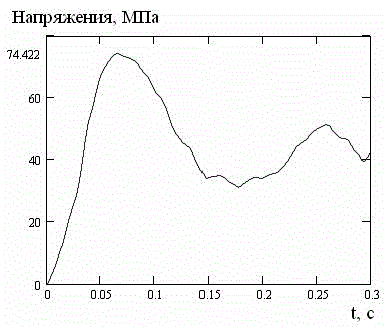
Рисунок 6 – Интенсивность напряжений при гидродинамической нагрузке для глубиныh=1 м
Анализ графиков показывает, что для глубины h=1 м величина гидродинамической нагрузки не является критичной. Полученные численные значения величин свидетельствуют о том, что исследуемая плита будет претерпевать упругие деформации и сохранит свою целостность.
На рис. 7 и 8 представлены перемещения и интенсивности напряжений для глубины h=2 м. Анализ графиков показывает, что для глубины h=2 м по сравнению с глубиной h=1 м не только величина гидродинамической нагрузки, а и величины перемещения и интенсивности напряжений увеличились на 50 %. Однако, абсолютные значения этих величин еще недостаточны для разрушения конструкции.
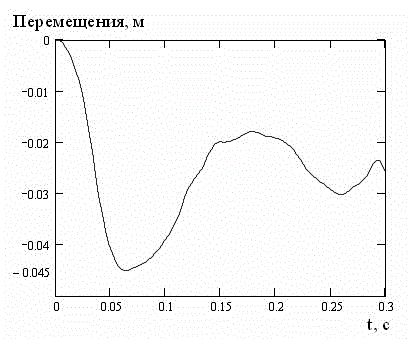
Рисунок 7 – Перемещения при гидродинамической нагрузке для глубины h=2 м
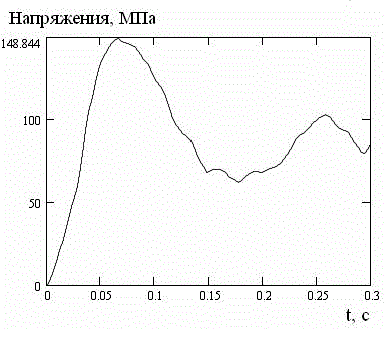
Рисунок 8 – Интенсивность напряжений при гидродинамической нагрузке для глубины h=2 м
На рис. 9 и 10 представлены перемещения и интенсивности напряжений для глубины h=3 м. Анализ графиков показывает, что для глубины h=3 м по сравнению с глубиной h=1 м величины перемещения и интенсивности напряжений увеличились примерно на 34 %, а по сравнению с глубиной h=2 м – на 67 %. Абсолютные значения этих величин превысили значения, полученные при расчете импульсного деформировании плиты, что позволяет сделать вывод о частичном разрушении конструкции.
Таким образом, использование результатов расчетов соисполнителей проекта позволило провести исследования динамики элементов морских сооружений под действием ударно-волновых нагрузок на новом уровне и получить ряд новых результатов.
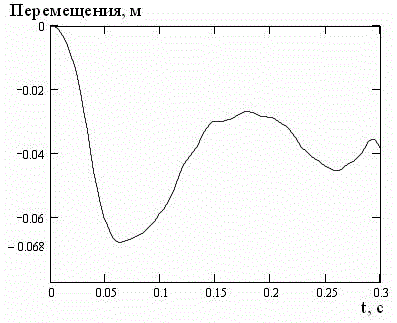
Рисунок 9 – Интенсивность напряжений при гидродинамической нагрузке для глубины h=3 м
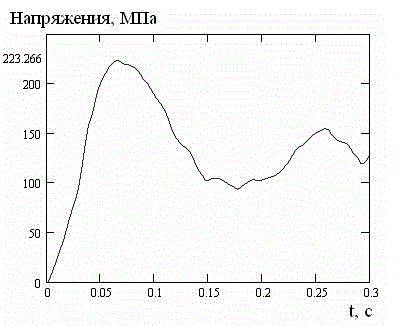
Рисунок 10 – Интенсивность напряжений при гидродинамической нагрузке для глубины h=3 м
Представленная методика позволяет определить напряженно-деформированное состояние плиты под действием реальной ударно-волновой или гидродинамической нагрузки, а также сделать выводы о степени разрушения конструкции. Решение задачи проводится на основе адаптивного конечно-разностного метода.
Работа выполнена при поддержке совместного проекта "Численное моделирование нестационарного взаимодействия сложных упругих конструкций с жидкостью или газом" фундаментальных исследований ученых учреждений НАН Украины и Сибирского отделения РАН.>
1. Воробьев Ю.С., Чернобрывко М.В., Ярыжко А.В. Динамика оребренных элементов конструкций при ударно-волновом воздействии // Тези додоповідей Міжнар. наук.-техн. конф. «Актуальні проблеми механіки суцільного середовища і міцності конструкцій». – Дніпропетровськ, 2007. – С. 246-248.
2. Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х т.: Т.2.: Пер. С англ. – М.: Мир, 1991. – 552 с.
3. Воробьев Ю.С., Чернобрывко М.В. Об особенностях моделирования ударно-импульсного нагружения оболочек и пластин. Механіка та машинобудування. – 2006.– № 1 – C. 39-45.
4. Лук’яненко С.О. Адаптивні обчислювальні методи моделювання об’єктів з розподіленими параметрами. – Київ: Політехніка, 2004. – 234 с.
5. Чернобрывко М.В. О применимости упрощенных математических моделей для расчетов конструкций при импульсном деформировании // Физические и компьютерные технологии в народном хозяйстве. Тр. 11-й МНТК. – Харьков, 2005.– C.264–266.
6. Ю.С. Воробьев, М.В. Чернобрывко, Л. Крушка Особенности численного анализа скоростного деформирования элементов конструкций под действием локальных импульсных нагрузок. // IX Konferencja Naukowo-Techniczna «Programy MES w komputerowym wspomaganiu analizy, projektowania i wytwarzania», Warsaw (Poland), 2005.– P.545-551.
7. Стурова И.В. Влияние переменной глубины жидкости на нестационарное поведение упругой пластины, плавающей на мелководье // Проблемы механики сплошных сред и физики взрыва: Тез. докл. Всерос. конф., посвященной 50-летию Института гидродинамики им. М.А. Лаврентьева СО РАН. – 2007. – С. 158-159.