Разрушение в грануляции

  Прочность материала можно интерпретировать как сопротивление материала остаточной деформации и разрушению во время создания напряжения. Это нормальное явление материала, чтобы достичь максимально допустимого значения напряжения прежде, чем произойдет разрушение. Таким образом, распределение напряжений, возникающих, когда материал нагружается, играет значительную роль в определении поведения разрушения материала. Для однородных упругих сфер (частиц), контактирующих с внешними телами, классические теории Hertz [1] и Lurje [2] могут быть наложены на распределение напряжений в сфере Кайнцлер и Schmitt [3]. Совсем недавно, Shipway and Hutchings [4] получили численные значения упругих напряжений, возникающих в сфере при одноосном сжатии и свободном ударе об плиту. Если сфера деформируется не упруго, предполагается, что существует огромное отличие в результате поля напряжений в упругом случае. Катастрофическое разрушение твердых частиц будет происходить после того, как будет превышено максимально допустимое значение напряжения материала. Виды отказов можно разделить на три категории: хрупкие, полу-хрупкие и вязкие в зависимости от степени пластической деформации, испытываемой материалом при разрушении. Хрупкое разрушение происходит без значительной пластической деформации, тогда как существенная пластическая деформация присутствует в материале, который разрушается пластично. Промежуточный случай, когда хрупкое разрушение происходит на границах небольшой, пластически деформированной области, называется полу-хрупкий отказ [5]. Тем не менее, в то время как эти описания подходят для однородных сплошных твердых частиц, где местные напряжения могут быть переданы всему объему материала, они недостаточны для описания разрушения гранулированных твердых веществ. Гранулированный материал представляет собой скопление из мелких частиц, удерживаемых вместе межчастичными связями. Межчастичные связи внутри твердых гранул могут быть разорваны, в результате чего, частицы в точке приложения нагрузки, станут свободными и нагрузка может быть передана всей однородной системе [6]. Из этого можно сделать вывод, что прочность гранул регулируется механизмами межчастичного склеивания, а не силой отдельных составных частиц. Кроме этого, передача нагрузки в гранулированную среду влияет на плотность частиц. Очевидно, что воспринимаемая прочность гранул будет функцией от типа и концентрации их внутренних связей. Прежде чем дальше рассматривать прочность гранул, стоит пересмотреть межчастичные силы, которые могут влиять на прочность гранул. Эти межчастичные связи были рассмотрены Rumpf [7], Schubert [9]. Различные типы связей, которые могут существовать в гранулах могут быть классифицированы следующим образом.

Силы вследствие неподвижных пленок. Тонкий неподвижный жидкостный слой может быть сформирован на поверхности частиц благодаря достижению критического уровня уплотнения гранул или нехватки связующего за счет испарения. Перекрытие из неподвижного слоя жидкости между первичных частиц производит таких связей, сила . Прочность этих связей зависит от площади контакта и свойств связующего , такие как предел прочности на разрыв слоя жидкости.

Силы вследствие подвижных жидких мостов. С увеличением содержания жидкости в грануле, жидкость между первичными частицами, как правило, перемещается, образуя жидкие мосты. Типично, что влажность гранул возрастает с увеличением содержания жидкости до точки, в которой гранула насыщенна и жидкие мостики больше не существуют.

Силы из-за твердых мостов. Твердые мостики могут быть образованы, например, через химические реакции, кристаллизацию, затвердевания и спекания связующего. Если существуют такие типы связей, они, как правило, являются прочностным определением связи.

Образование твердых мостов между первичными частицами, как правило, не применимы в случае, когда гранулы влажные. Также предполагается, что блокировка этого эффекта имеет значение только в нескольких конкретных случаях. Поэтому широко признано, что статическая прочность влажных гранул определяется главным образом жидкостно- мостовых сил между первичными частицами. Это происходит из-за сложных взаимодействий этих сил.

В итоге, пытаясь понять неспособность гранулирования материалов, были разработаны две принципиальные парадигмы [10]. Первая приписывается Rumpf [7] и утверждает, что гранулы не удаются при одновременном разрыве всех связей вдоль плоскости трещины. Кроме того, Кендалл [9] утверждал, что гранулы разрушались из-за появления и распространения трещин, и адаптировал механику разрушения для описания этого.

Rumpf разработал классическую модель для прогнозирования статической прочности гранул на разрыв. С учетом гранул под действием приложенных нагрузок, он отметил, что разрушение гранул в основном вызвано растягивающим напряжением, осуществляемом в агрегате. Теоретический предел прочности на разрыв гранулы предлагают считать суммированием всех сильных межчастичных связей по всей поверхности разрушения. Подразумеваемым предположением в этом анализе являются межчастичные связи по всей поверхности разрушения, разрываемые одновременно в процессе разрушения. Это приводит к выводу следующего выражения для теоретической прочности гранул – растяжение, σ_t, в общем виде:

где n – среднее число межчастичных связей на единицу площади поперечного сечения гранулы и F – среднее усилие, требуемое, чтобы разделить их. Было обнаружено, что межчастичные связи твердой фракции гранул и размеры составных частиц равномерно распределяются по первичным частицам. Таким образом, уравнение можно переписать в виде:

где ε и D – доля пустот внутри гранулы и составной диаметр частиц, соответственно. Тем не менее, составляющие частицы реальных гранул зачастую полидисперсные и несферические. В отношении этой проблемы предлагается D заменить на средний диаметр, например поверхностно-средний объемный диаметр из составных частиц [10]. Первое и третье уравнения и применимы к гранулам с различными механизмами внутренней связи, что приводит к различным выражением для F. Для влажных гранул, где первичные частицы удерживаются с помощью жидких мостов, модель определяется как:

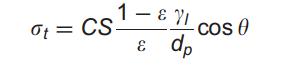
где С – константа материала (для однородных сфер С = 6), S – насыщенность жидкостью, ε – доля пустот внутри гранулы, d_p – средний диаметр поверхности частиц, γ₁ – поверхностное натяжение жидкости и у угол контакта жидкость-твердое тело.

Список источников

1. H. Hertz, Miscellaneous Papers by H. Hertz,, Macmillan, London, 1896
2. A. Lurje, Raümliche Probleme der Elastizitätstheorie, Akademie-Verlag, Berlin,1963
3. R. Kienzler, W. Schmitt, Powder Technol. 61 (1) (1990) 29–38.
4. P.H. Shipway, I.M. Hutchings, Philos. Mag. A (Physics of Condensed Matter, Defects and Mechanical Properties) 67 (6) (1993) 1389–1404.
5. J. Subero, M. Ghadiri, Powder Technol. 120 (3) (2001) 232–243
6. P. Kapur, D. Fuerstenau, J. Am. Ceram. Soc. 50 (1967) 14–19.
7. H. Rumpf, in Agglomeration, Interscience, New York, 1962.
8. H. Schubert, Powder Technol. 11 (2) (1975) 107–119
9. P. Sherington, R. Oliver, Granulation, Heyden, London, 1981.
10. P.C. Knight, Powder Technol. 119 (1) (2001) 14–25.