The strength of a material can be interpreted as the resistance of the material to permanent deformation and fracture during a stressing event. It is normal to attribute material strength to be a maximum allowable stress value before fracture occurs. Hence, the stress distribution arising when a material is loaded plays a significant role in determining the fracture behaviour of the material. For a homogeneous elastic sphere (the proverbial particle) in contact with external bodies, classical theories of Hertz [1] and Lurje [2] can be superposed to the overall stress distribution within the sphere Kienzler and Schmitt [3]. More recently, Shipway and Hutchings [4] derived numerical values for elastic stress ?elds developed in spheres under uniaxial compression and free impact against a platen. If the sphere is deformed inelastically, it is expected that there is dramatic departure of the resulting stress field from the elastic case. Catastrophic failure of solid particles will take place once the maximum allowable stress of the material is exceeded. The failure modes can be classified into three categories viz. brittle, semi-brittle and ductile failures depending on the extent of plastic deformation experienced by the material during fracture. Brittle failure occurs without significant plastic deformation whereas substantial plastic deformation can be found in material fails in a ductile manner. An intermediate case where brittle fracture occurs at the boundaries of a small plastically deformed region is termed semi-brittle failure [5]. However, while these descriptions are suitable for homogeneous continuum solid particles where local stresses can be transmitted throughout the entire volume of material, they are insufficient to describe the failure of granular solids. Granular material is a cluster of small particles held together by interparticle bonds. The interparticle bonds within a granular solid may be ruptured causing the particles at the point of load application to be sheared apart before the load can be transmitted throughout the solid as in a homogenous elastic system [6]. From this it can be concluded that the strength of a granular medium is governed by interparticle bonding mechanisms rather than the strength of individual constituent particles. Furthermore, the load transmission in a granular medium is affected by its internal particle packing. It is clear that the perceived strength of a granule will be a function of the nature and concentration of its internal bonds. Before looking in more detail at granule strength, it is worth reviewing the interparticle forces that are likely to be contributing to a granule’s strength. These inter-particle adhesive or bonding forces have been reviewed by Rumpf [[7], Schubert [8] and Sherington [9]. The different types of bonds that may exist within a granule can be classified as follows.
Forces due to immobile films. A thin immobile liquid layer can be formed on the surface of primary particles due to reasons such as granule reaching a critical level of compaction or excess binder removal through evaporation. Overlapping of the immobile liquid layer between primary particles produces this bonding force. The strength of these bonds is dependent on contact area and the properties of the binder such as the tensile strength of the liquid layer.
Forces due to mobile-liquid bridges. With increasing liquid content in the granule, the liquid between primary particles tends to be mobile, forming liquid bridges. In this case, adhesion forces arise from surface tension forces at the liquid/air interface- and hydrostatic-suction pressure in the liquid bridge. Typically it is found that wet-granule strength increases with increasing liquid content up to the point at which the granule is saturated and the liquid bridges no longer exist.
Forces due to solid bridges. Solid bridges can be formed, for example, through chemical reactions, crystallisation, binder solidification and sintering. If these types of bonds exist, they will typically be the primary strength determining bonds.
In addition, formation of solid bridges between primary particles is usually not applicable in the case of wet granules. It is also then assumed that the interlocking effect is only significant in a few specific cases. It is therefore widely accepted that the static strength of wet granules is determined principally by liquid-bridge forces between primary particles. It is due to the complicated interactions of these forces that it is difficult to define granule strength.
As a result of trying to understand the failure of granular materials, principally two theoretical paradigms have developed[10]. The first is attributed to Rumpf[7] and considers that a granule fails by simultaneous rupture of all the bonds along a fracture plane. Alternatively, Kendall [9] argued that a granule failed through crack nucleation and propagation, and adopted fracture mechanics to describe this.
Rumpf developed a classical model for predicting the static-tensile strength of granules. Considering a granule under the action of applied loads, he pointed out that fracture of the granule is mainly caused by the tensile stress generated within the assembly. The theoretical tensile strength of a granule is suggested to be the summation of all the interparticle bond strengths across the fracture surface. The implicit assumption in this analysis is all the interparticle bonds across the fracture surface ruptured simultaneously during the fracture process. This leads to the derivation of the following expression for theoretical granule-tensile strength, σt, in its general form

where n is the average number of interparticle contacts per unit area across the granule cross-section and F the mean force required to separate them. It is found that n scales with granule-solid fraction and size of the constituent particles with a uniform primary particle size distribution. Therefore, equation can be rewritten as follows:

where ε and D are the intra-granular void fraction and constituent-particle diameter, respectively. Nevertheless, the constituent particles of real granules are often poly-disperse and non-spherical. In respect to this problem, it is proposed that D in the foregoing should be substituted with the mean diameter, for instance the surface-volume mean diameter, of the real constituent particles [10]. Equations (1) and (3) are applicable to granules with different internal bonding mechanisms, which results in different expression for F. For wet granules, where primary particles are held together with liquid bridges, the model is given as:
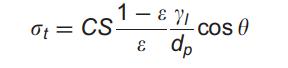
where C is a material constant (for uniform spheres C = 6), S the liquid saturation, ε the intra granular void fraction, dp the surface average diameter of primary particles, γ1 – the liquid surface tension, and y the liquid–solid contact angle.
References
- H. Hertz, Miscellaneous Papers by H. Hertz,, Macmillan, London, 1896
- A. Lurje, Raümliche Probleme der Elastizitätstheorie, Akademie-Verlag, Berlin,1963
- R. Kienzler, W. Schmitt, Powder Technol. 61 (1) (1990) 29–38.
- P.H. Shipway, I.M. Hutchings, Philos. Mag. A (Physics of Condensed Matter, Defects and Mechanical Properties) 67 (6) (1993) 1389–1404.
- J. Subero, M. Ghadiri, Powder Technol. 120 (3) (2001) 232–243
- P. Kapur, D. Fuerstenau, J. Am. Ceram. Soc. 50 (1967) 14–19.
- H. Rumpf, in Agglomeration, Interscience, New York, 1962.
- H. Schubert, Powder Technol. 11 (2) (1975) 107–119
- P. Sherington, R. Oliver, Granulation, Heyden, London, 1981.
- P.C. Knight, Powder Technol. 119 (1) (2001) 14–25.