Реферат за темою випускної роботи
Зміст
- Вступ
- 1 Розвиток монорейкового транспорту
- 2 Аналіз попередніх досліджень за темою роботи
- 3 Актуальність теми
- 4 Мета та завдання
- 5 Дослідження параметрів підвісного составу
- 5.1 Математична модель руху
- 5.2 Прийняті допущення
- 5.3 Побудова руху при заданих параметрах в системі Mathcad
- Висновки
- Перелік посилань
Вступ
У розвинених країнах дуже широко використовується підвісний монорейковий транспорт. З його допомогою вирішуються проблеми надземної розв'язки транспортних потоків. Зарубіжна і вітчизняна практика показує успішні результати в застосуванні монорейкового транспорту не тільки як надземного, але і як підземного. При експлуатації в шахті монорейкового транспорту дозволені або спрощуються завдання при перевезенні людей і допоміжних матеріалів по виробках. Особливою його перевагою є практичність у застосуванні і безпека.
Існують дві системи монорейкових доріг: з канатною і локомотивною тягою. З них слід віддати перевагу другій, так як вона забезпечує дуже високу безпеку. Також при експлуатації доріг з канатною тягою виникають проблеми можливості роботи на розгалужених лініях і перевезень на далекі відстані.
Зараз почали впроваджувати нововведення, які забезпечують безпечну роботу гірників. Впровадження монорейкового транспорту дозволило різко скоротити обсяги ручної праці на доставних роботах, зменшити травматизм, пов'язаний з перевантаженнями, причіпними пристроями рухомого складу, маневрами на розминовках, обривами каната, сходом транспортних судин з рейкової колії, вирішити проблему доставки людей до місця ведення робіт і назад до виходу на поверхню. Завдяки перевезенню людей по гірничих виробках монорейковою дорогою, з дотриманням чіткого графіка доставки, тепер робочим немає необхідності йти пішки або їхати на засобах, не призначених для перевезення людей. Застосування монорейкових дизелевозів в монтажних камерах дозволило різко скоротити терміни і знизити трудомісткість монтажно–демонтажних робіт.
Монорейкова дорога – це транспортна система, в якій вагони переміщаються по балці–монорейці, встановленої на окремих опорах або естакаді. Однак таке визначення занадто розпливчасто. Реально монорейкові дороги підрозділяються на ряд дуже специфічних різновидів, спільне між якими – тільки монорейка.
1 Розвиток монорейкового транспорту
Перша згадка про монорейку з'явилося в 1820 році в Росії. Тоді мешканець села Мячково в Підмосков'ї Іван Ельманов побудував «Дорогу на стовпах» – по верхньому подовжньому брусу котилися вагонетки, які тягнули коні. Трохи пізніше, незалежно від російського винахідника, монорейка схожої конструкції був винайдена у Великобританії Генрі Робінзоном Пальмером. Він запатентував свій винахід 22 листопада 1821 року. У 1824 році у Великобританії була побудована перша діюча монорейка. Вона використовувався на військово–морської верфі виключно для перевезення вантажів. Перша пасажирська монорейка в світі була відкрита 25 червня 1825 року.
Після цього протягом приблизно півстоліття нічого нового в області будови монорейки не відбувалося. Спроби створити працездатну монорейку, тепер вже на паровій тязі, поновилися в кінці XIX століття. Відомо, що в 1872 році на політехнічній виставці в Москві демонструвалася ділянка монорейкової дороги конструкції інженера Лярского.
Загалом в кінці XIX століття монорейка була частим гостем на різноманітних виставках. У 1872 році монорейка на кабельній тязі демонструвалася в Ліоні, в 1891 році в Сент–Луїсі демонструвалася монорейка з вагонами на зразок трамвайних.
У той же час створення діючої, працездатної монорейки виявилося набагато більш складною справою. У XIX столітті було створено величезну кількість конструкцій монорейки, але більшість з них так і залишилися на папері, а ті, які були реалізовані, не відрізнялися довголіттям. У 1878 році почала діяти парова монорейка, що з'єднує Брадфорд і Гілмор (Пенсільванія). Їі довжина становила 6,4 км. Ця монорейка створювалася для перевезень промислового устаткування, але вона також перевозила пасажирів. Брадфордська монорейка закрилася незабаром після серйозної катастрофи, що трапилася 27 січня 1879 року, коли загинув машиніст монорейки і три його пасажири.
З розвитком електротехніки на монорейках стали використовувати електричний привід. Одна з перших електричних монорейкових доріг, відома як Enos Electric Railway, була побудована в 1887 році в Грінвіль, Нью–Джерсі.
Як вже було зазначено вище, незважаючи на активні пошуки, створити монорейку, здатну бути повноцінним транспортним засобом, в XIX столітті так і не вдалося. Єдина успішна монорейка тієї епохи – побудована в Ірландії в 1888 році монорейка, з'єднувала Баллібуніон і Лістоуел. Вона проіснувала до 1924 року. Однак поширення ця конструкція не отримала.
Перші монорейки на кінній тязі були підвісними. Парові монорейки мали своєрідну напівпідвесну конструкцію: склад спирався на несучу рейку, стабільність забезпечувалася бічними напрямними рейками. Поперечний розріз такого шляху нагадував букву «А», де верхня точка відповідає несучій рейці, а точки з'єднання бічних сторін і поперечної перекладини – направляють. З появою електричних монорейок знову стала використовуватися підвісна компоновка
Однак пропонувалися і більш незвичайні конструкції. У 1894 році в США була побудована монорейкова залізниця Boynton Unicycle Railway. На цій дорозі поїзд спирався на одну несучу рейку, зверху ж проходил підтримуюча дерев'яна рейка. Основним недоліком такої дороги було те, що на поворотах через інерції ("відцентрової сили") на підтримуючу рейку діяли високі сили.
В кінці XIX століття з'явилися опорні монорельси. У 1886 році в США була побудована дослідна монорейка такого типу, Meigs Monorail, але в ті часи поширення така конструкція не отримала. Що з'явилася в Америці система капітана Мейгса складається з двох рейок, розташованих одна над іншою прямовисно і підтримуючих металевими колонами. У підставу цієї системи покладена ідея зосередження всього тиску, переданого на шлях рухомим складом, в осьовій лінії поїзда. Кожен вагон спочиває на парі поворотних візків, підтримуваних двома напрямними горизонтальними колесами і чотирма похилими колесами, з клиноподібними жолобами по обіду. Останні котяться на двох рейках квадратного перетину, прикріплених до нижніх поясів гратчастих балок, створюючи нижню будову колії. Горизонтальні колеса локомотива служать, разом з тим, для передачі руху, а тому ці колеса, для збільшення тиску, притискаються особливими пристосуваннями до рейок.
2 Аналіз попередніх досліджень за темою роботи
Тяговий пристрій монорейкового складу дозволяє реалізувати силу тяги і гальмування (деякою мірою) за рахунок фрикційного зв'язку приводних коліс з монорейкою, які можуть розташовуватися під монорейкою або збоку. Для шахтних умов, коли потрібні значні зусилля притиснення, більш кращим є установка з вертикальною віссю обертання і примусовим притиском до вертикальної стінки монорейки по обидві сторони. Подібна схема використана у вітчизняних складах ДМВ–7,2–ДМД, а також зарубіжних – "Шарф"DZ 66–3",
ZL – 90 (ПНР) [25], де використовується електричний, гідравлічний або пневматичний приводи [3].
Зазначені машини дозволяють створити універсальний транспорт, особливо для допоміжних вантажів вугільних шахт. При цьому транспортування може здійснюватися без перевантажень і перечіпов на значні відстані (до 4...6 км). В цьому напрямку проведено ряд робіт.
Найбільш докладно результати наукових досліджень по створенню монорейкових составів наводяться в роботах B.C. Берсенєва [4], присвячених розробці теоретичних основ тягових пристроїв з автоматичним регулюванням тиску приводних коліс на рейки у залежності від опору руху поїзда.
Досліджені особливості врівноваження нормальних реакцій рейки, доданих до приводних коліс, беручи до уваги, що сила тяжіння всього тягового пристрою у багато разів менше цих реакцій, розглянуто умови, за яких забезпечується рівновага, досліджено вплив власних опорів тягового механізму на процес створення тягового зусилля. Виходячи з характеру і співвідношення зовнішніх сил, визначено особливості механізму.
Дан опис типів тягових пристроїв, проаналізовано особливості роботи різних конструкцій, отримані методи розрахунку і визначені коефіцієнти корисної дії.
Як зазначено автором, в роботі [5] не розглядаються питання вписування тягового пристрою в закруглення колії, а також не враховується його бокове розгойдування, що неминуче виникає при русі по монорейці. У роботах Л.І. Айзенштока [1, 2] наведено результати дослідження профілю монорейкового шляху як джерела коливань рухомого складу і встановлені аналітичні залежності збурень і їх параметри. Визначені фактори, що впливають на величину бічних відхилень монорейкового складу.
Однак у цих роботах не враховується вплив місця розташування і ступінь притиснення приводних коліс складу до монорельсу.
Напрямком робіт А.С. Веткина були дослідження процесу вписування рухомого складу. Отримані закономірності не можуть бути використані для визначення параметрів тягового пристрою, так як вони ставляться до причіпної частини складу. Слід зазначити, що, незважаючи на велику кількість публікацій, присвячених питанням створення монорейкових составів, опублікованих в радянській і зарубіжной літератури, не існує певної методики, що дозволяє однозначно визначити основні параметри монорейкових доріг. Перші спроби в узагальненні цих питань належать В.М. Григор'єву. На підставі широких досліджень ім виявлено основні конструктивні схеми тягових пристроїв, визначені раціональні області застосування монорейкових доріг, розглянуті питання впливу конструктивних особливостей монорейкового складу на параметри руху, про можливу швидкість руху поїзда і достатній потужності складу, а також про спосіб регулювання приводу.
Дослідження, які виконані Л.Г. Желтухіним, присвячені знаходження оптимальних параметрів підвішування рухомого складу шахтної підвісної монорейкової дороги, виявлення характеру взаємодії вагонетки з стиками монорейки. У зазначених роботах не відображені питання взаємодії приводних коліс тягового пристрою з монорейкою, а це не дозволяє їх використовувати в цій роботі. На підставі аналізу конструкцій монорейкових тягачів З.М.Мерецьким виявлено основні вимоги до їх конструкцій, визначений раціональний тип приводу.
Проведені дослідження М.В. Чашко присвячені створенню рудничних монорейкових тягачів з лінійним індукційним двигуном. Як показали дослідження, доцільно застосовувати на швидкостях, значно більших, ніж 2 м/с, що зараз для шахтних умов є складним. При цьому потрібно такий стан рейкового шляху, де профіль не мав би перегинів і перевищень в стиках. Основним достоїнством складу з лінійним двигуном є те, що його тягове зусилля не залежить від коефіцієнта зчеплення привідного елемента з рейковим шляхом. Коефіцієнт зчеплення - величина непостійна, що залежить від багатьох умов. У даний час існує багато гіпотез, що пояснюють фізичний процес реалізації тягового зусилля привідними колесами. Проте, всі вони суперечливі і не дозволяють визначити значення розрахунковим шляхом, тобто чисто теоретично. Для тягових розрахунків прийнято використовувати експериментальні дані. Раніше у зазначених роботах наведено результати досліджень коефіцієнта зчеплення приводних коліс з монорейкою, причому кожен з авторів дає його значення реально для індивідуального експерименту, не проводячи відповідної статистичної обробки, не враховуючи зовнішніх умов, що впливають на значення цього коефіцієнта. У зв'язку з цим, вказані значення можуть бути використані в малому ступені як узагальнених для тягових розрахунків при різних умовах експлуатації монорейкових доріг. Найбільш широко проблеми застосування монорейкових доріг у промисловості викладені в роботах [2]. Наведені дані застосовні для транспортних засобів, що працюють у стабільних умовах, але для важкого стану транспортної дороги, властивого вугільним шахтам, потребують перевірки і підлягають уточненню. Крім цього, у зазначених роботах не приведені рекомендації по вибору жорсткої бази тягового пристрою, діаметра і числа приводних коліс, а також типу притискного пристрою.
Певний інтерес представляють роботи інституту ВНІІгідровугілля, присвячені створенню підвісних монорейкових составів з дизельним приводом. За період з 1967 року по 1977 рік розроблені три типи дизелевозов ДМХ, які мають тягове зусилля 7, 30 і 55 кН. Останній (ДМВ 7) має потужність 55,7 кВт і призначений для доставки вантажів масою до 7 т по виробкам з кутами нахилу до 45°. В описаних роботах основним напрямком є створення тягового пристрою з об'ємним гідроприводом і недостатньо опрацьованим питанням щодо безпосереднього зв'язку тягового блоку з монорейкою, розроблений ряд методик, що дозволяють в широких межах робити вибір параметрів. Однак для обґрунтованого створення завершеною конструкції монорейкового складу їх недостатньо.
Завдання про перевернутий тяговий пристрій (маятник) з вібруючою точкою підвісу прийнято називати завданням Капіци. В його роботах [6, 7] на основі наближеного рішення теоретично обґрунтовано, що, починаючи з деякою певної частоти вертикальних коливань точки підвісу, Тяговий пристрій стає стійким у своєму верхньому положенні. Більш того, П.Л. Капіца запропонував механічну конструкцію для демонстрації такого ефекту, отримавши тим самим експериментальне підтвердження свого результату. Проте, ще задовго до Капіци в 1908 році англійський математик A. Stephenson також розглядав таку задачу [8,9]. Їм було показано, що досить просто утримувати жердину у вертикальному положенні, вібруючи точку опори по вертикалі, а не перемістити її з боку в бік, як це зазвичай роблять, в горизонтальній площині. Слід зазначити також ще більш ранній результат, представлений в книзі лорда Релея [10], про втрату стійкості нижнього положення рівноваги при горизонтальних коливаннях підвісу з певною частотою. У 1950 році, за рік до виходу статей [6,7], М.М. Боголюбов у своїй роботі [11] викладає теорію методу усереднення, дотримуючись монографій [12,13], максимально пристосовуючи його для практичних застосувань. Тут також зустрічається приклад нашого пристрою з вібруючою точкою підвісу і для нього отримана оцінка частоти, що гарантує стійкість верхнього положення тягового пристрою, що збігається з результатом П.Л. Капіци. Однак обидва вчених прийшли до цього результату незалежно і різними методами. Безперечна заслуга П.Л. Капіци полягає в тому, що він експериментально продемонстрував ефект вібраційної стабілізації, що породило підвищений інтерес до даної задачі, і кількість робіт, присвячених цій тематиці, зросла багаторазово.
До 1950 р. можна відзначити роботи німецьких учених, які досліджували рух тягового пристрою при швидких вібраціях точки підвісу з малою амплітудою по вертикалі [14], по горизонталі [15], а також в довільному напрямку [16]. Аналіз стійкості верхнього положення тягового пристрою при коливаннях точки підвісу уздовж довільно вибраної осі був виконаний І.Г. Малкіним [17]. Більш складні траєкторії руху підвісу були запропоновані в монографіях [18,19], де розглядалися переміщення не тільки по вертикалі або по похилій прямій, але також і еліптичні траєкторії. При цьому в роботі [18] був розроблений апарат вібраційної механіки на основі методів усереднення і введено поняття квазірівноваги коливальних систем, що позначає стаціонарність повільної складовою вирішення таких систем. Строгий аналіз стійкості відносних положень рівноваги тягового пристрою на вертикалі в нелінійній постановці при гармонійних вертикальних вібраціях точки підвісу довільної частоти і амплітуди був виконаний у роботі [20]. У монографії [21] були запропоновані алгоритми низькочастотної лінійної стабілізації, які дозволили виявити ефект низькочастотної стабілізації системи лінійного наближення тягового пристрою у верхньому положенні. У роботі [22] досліджено вплив в'язкого тертя на величину критичної частоти стабілізації верхнього положення рівноваги.
У даній роботі досліджується можливість за допомогою управління рухом точки підвісу забезпечити рівновагу тягового пристрою в довільному наперед заданому похилому положенні або коливання як завгодно малою амплітудою щодо вибраного положення.
3 Актуальність теми
Питання про монорейкових дорогах, особливо з локомотивною тягою є однією з поширених, що розвиваються тем доповідей, наукових робіт, досліджень в наш час. Монорейкові дороги відіграють важливу роль у розвитку гірничої промисловості в усьому світі. Але не всі країни можуть впроваджувати новітні установки в промисловість, також вся система має безліч недоробок. Якщо не розвивати і не покращувати характеристики експлуатації даного виду транспорту, то втративши свою цінність, його перестануть використовувати. Безліч вчених зробили свій найцінніший внесок у розвиток монорейкового транспорту. Деякі з них: Докт. техн. наук B.C. Берсенєв, канд. техн. наук Л.І. Айзеншток, А.С Вєткін, Л.Г. Желтухін, В.М. Григор'єв, В.В. Бухановський та інші. Найбільш докладно результати наукових досліджень по створенню монорейкових локомотивів наводяться в роботах B.C. Берсенєва. Основним напрямком робіт А.С. Вєткіна з'явилися дослідження процесу вписування рухомого складу. Отримані закономірності не можуть бути використані для визначення параметрів тягового пристрою, так як вони ставляться до причіпної частини складу. Слід зазначити, що, незважаючи на велику кількість публікацій, присвячених питанням створення монорейкових локомотивів, опублікованих в радянській та зарубіжній літературі, не існує певної методики, що дозволяє однозначно визначити основні параметри монорейкових доріг. Перші спроби в узагальненні цих питань належать В.М. Григор'єву. На підставі широких досліджень виявлено основні конструктивні схеми тягових пристроїв, визначено раціональні області застосування монорейкових доріг, розглянуті питання впливу конструктивних особливостей монорейкового локомотива на параметри руху, про можливу швидкість руху поїзда і достатньої потужності локомотива, а також про спосіб регулювання приводу.
4 Мета та завдання
Мета роботи - обґрунтувати параметри монорейкового составу для проектування пристрою запобігає бічне розгойдування, що забезпечить підвищення швидкостей пересування составів і збільшить термін служби систем підвішування і попередить викривлення шляху монорейки.
Для досягнення даної мети поставлені такі основні завдання:
• встановити основні фактори, що впливають на розгойдування;
• скласти математичну модель руху монорейкового составу;
• обґрунтувати параметри підвісної монорельсового шляху.
Практична цінність даної роботи полягає в можливості більш широкого застосування монорейкового транспорту для допоміжних робіт на гірничому підприємстві, збільшення швидкості руху наявних монорейкових составів.
5 Дослідження параметрів підвісного составу
5.1 Математична модель руху
Розглянемо плоский рух екіпажу, що складається з матеріальної точки маси m і невагомого стрижня довжини  , на якій підвішена ця точка, в полі сили тяжіння. При цьому точка підвісу не закріплена, а може рухатися певної (заданої або обраній) траєкторії. Передбачається відсутність будь–або сил тертя і опору. Становище екіпажу будемо визначати кутом
, на якій підвішена ця точка, в полі сили тяжіння. При цьому точка підвісу не закріплена, а може рухатися певної (заданої або обраній) траєкторії. Передбачається відсутність будь–або сил тертя і опору. Становище екіпажу будемо визначати кутом  . Нехай задано деякий положення
. Нехай задано деякий положення  у якому він знаходиться в початковий момент з нульовою кутовою швидкістю. Завдання полягає в знаходженні закону руху точки підвісу
у якому він знаходиться в початковий момент з нульовою кутовою швидкістю. Завдання полягає в знаходженні закону руху точки підвісу 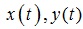 , що не дозволяє екіпажу змінювати положення з плином часу, тобто забезпечити існування рішення
, що не дозволяє екіпажу змінювати положення з плином часу, тобто забезпечити існування рішення  .
.
Рівняння руху (рис. 5.1)при переміщенні точки підвісу екіпажу за законом  має вигляд
має вигляд
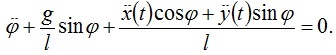 (1)
(1)
Важливий окремий випадок виникає, коли точка підвісу коливається уздовж деякої вісі, що утворює кут  з напрямком сили тяжіння. Позначивши зміщення точки підвісу вздовж цієї вісі
з напрямком сили тяжіння. Позначивши зміщення точки підвісу вздовж цієї вісі  , маємо
, маємо
.jpg) (2)
(2)
Рівняння коливань екіпажу (1) перетворюється до вигляду
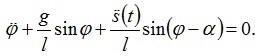 (3)
(3)
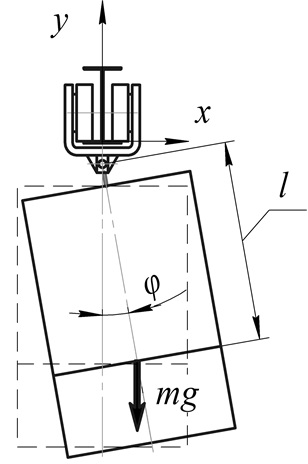
Рисунок 5.1 – Розрахункова схема розгойдування екіпажу
Так як верхнє  і нижнє
і нижнє  вертикальні екіпажу є положеннями рівноваги при нерухомому підвісі
вертикальні екіпажу є положеннями рівноваги при нерухомому підвісі  , то виключимо їх з подальшого розгляду і будемо припускати, що
, то виключимо їх з подальшого розгляду і будемо припускати, що  . Відзначимо лише, що для збереження вертикальних положень рівноваги екіпажу точка підвісу може пересуватися лише вздовж вісі Oy. Як випливає з [4],верхнє положення стає стійким при коливаннях підвісу вздовж вертикалі з частотою вище
. Відзначимо лише, що для збереження вертикальних положень рівноваги екіпажу точка підвісу може пересуватися лише вздовж вісі Oy. Як випливає з [4],верхнє положення стає стійким при коливаннях підвісу вздовж вертикалі з частотою вище  , де
, де  – амплітуда цих коливань.
– амплітуда цих коливань.
Умови існування рівноваги. Спробуємо знайти рух точки підвісу  коли
коли  . Функції x(t) та y(t) можуть розглядатися як управління в рівнянні (1). Як клас допустимих управлінь розглянемо безперервні двічі диференційовані функції. Тоді, враховуючи
. Функції x(t) та y(t) можуть розглядатися як управління в рівнянні (1). Як клас допустимих управлінь розглянемо безперервні двічі диференційовані функції. Тоді, враховуючи  рівняння (1) перетворимо до виду
рівняння (1) перетворимо до виду 
Звідки
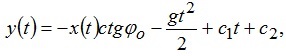 (4)
(4)
де  - константи, які визначаються з початкових значень швидкості та положення підвісу екіпажу.
- константи, які визначаються з початкових значень швидкості та положення підвісу екіпажу.
Обравши довільним чином x(t) з класу припустимих функцій, використовуючи рівняння (4) одержимо y(t), визначивши тим самим повністю рух точки підвісу. Таким чином, маємо систему управлінь x(t), y(t), що забезпечує нахилу рівновагу екіпажу. З'ясуємо, чи існують серед них обмежені.
Нехай x(t) – обмежена на напівінтервалі  функція. Тоді при
функція. Тоді при  в силу обмеженості x(t) величина
в силу обмеженості x(t) величина  згідно з (4) прагне до нескінченності. Отже, рух підвісу при
згідно з (4) прагне до нескінченності. Отже, рух підвісу при  не може бути обмеженим за обома координатами. Тим не менш можливий режим руху обмежений по y і необмежений по x, дозволяє екіпажу залишатися в нахиленому положенні (наприклад,
не може бути обмеженим за обома координатами. Тим не менш можливий режим руху обмежений по y і необмежений по x, дозволяє екіпажу залишатися в нахиленому положенні (наприклад,  ).
).
Спростимо тепер траєкторію руху підвісу. Будемо пересувати точку підвісу прямою (2), але розширимо клас припустимих функцій s(t). Цей клас буде містити функції, перші похідні яких (швидкості) можуть мати розриви першого роду в деяких точках. На проміжках між цими точками функції s(t) будуть, як і раніше, двічі диференційовані. У зазначених точках розриву розглянута механічна система зазнає імпульсного впливу.
Подальший розрахунок залежностей розписаний у роботі [5], звідси маємо, що при .jpg) знак
знак .jpg) збігається зі знаком
збігається зі знаком .jpg) , а при
, а при  – зі знаком
– зі знаком .jpg) . Ці знаки різні, оскільки виконана нерівність
. Ці знаки різні, оскільки виконана нерівність  . Отже, в силу безперервної залежності
. Отже, в силу безперервної залежності  від
від  існує деяке значення
існує деяке значення  , при якому приріст швидкості за період T буде дорівнювати нулю.
, при якому приріст швидкості за період T буде дорівнювати нулю.
Тепер розглянемо приріст s(t), він буде дорівнювати  . Очевидно, що залежно від початкового значення швидкості
. Очевидно, що залежно від початкового значення швидкості  , ми можемо отримати різні прирости
, ми можемо отримати різні прирости  . Виберемо початкову швидкість так, щоб це збільшення дорівнювало нулю. Позначимо
. Виберемо початкову швидкість так, щоб це збільшення дорівнювало нулю. Позначимо  . Тоді, обравши початкову швидкість
. Тоді, обравши початкову швидкість .jpg) рівною,
рівною,  отримаємо, що приріст s(t) буде нульовим.
отримаємо, що приріст s(t) буде нульовим.
Такі значення частоти  і початкової швидкості для s(t), такі, що координата підвісу s(t) і його швидкість за період повертаються до початкових значень. Отже, при цих значеннях рух підвісу s(t) буде періодичним і безперервним по t, а екіпаж буде здійснювати коливання відносно положення
і початкової швидкості для s(t), такі, що координата підвісу s(t) і його швидкість за період повертаються до початкових значень. Отже, при цих значеннях рух підвісу s(t) буде періодичним і безперервним по t, а екіпаж буде здійснювати коливання відносно положення  за законом
за законом  .
.
Візьмемо відстань від точки центру мас до точок підвісу складу довжиною  =800 мм і розглянемо його горизонтальне положення
=800 мм і розглянемо його горизонтальне положення  . Нехай вісь, вздовж якої коливається точка підвісу, утворює кут
. Нехай вісь, вздовж якої коливається точка підвісу, утворює кут .jpg) з напрямком сили тяжіння. Графіки руху точки підвісу екіпажу, що забезпечують гармонійні коливання близько горизонтального його положення з певною невеликою амплітудою
з напрямком сили тяжіння. Графіки руху точки підвісу екіпажу, що забезпечують гармонійні коливання близько горизонтального його положення з певною невеликою амплітудою  та графік залежності частоти
та графік залежності частоти  від
від  при періодичному русі s(t) точки підвісу зображені на рис. 5.3а.
при періодичному русі s(t) точки підвісу зображені на рис. 5.3а.
Рисунок 5.2 – Коливання екіпажу
(анімація: 4 кадра, 8 циклів повторення, 49,2 кб)
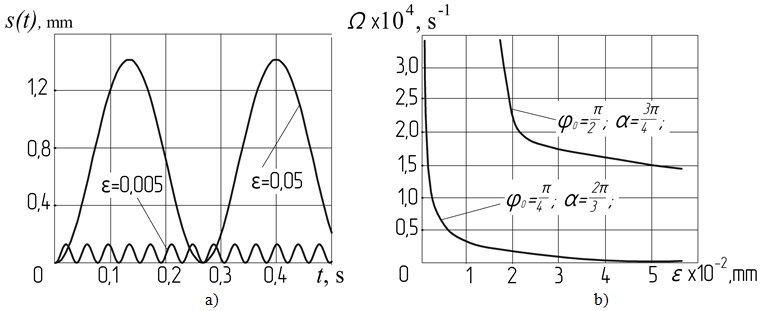
Рисунок 5.3 – Рух підвісу a) s=f(t) при  ; b) графік частоти
; b) графік частоти  .
.
На рис. 5.3б наведено графік залежності частоти  від
від  при періодичному русі s(t) точки підвісу. З якого ми бачимо, що частота
при періодичному русі s(t) точки підвісу. З якого ми бачимо, що частота  необмежено зростає при зменшенні амплітуди
необмежено зростає при зменшенні амплітуди  .
.
5.2 Прийняті допущення
Швидкість руху приймається постійною; колія ходових коліс, зважаючи на її малості, вважається рівною нулю; рама з приводом і маса екіпажу розташована по центру розглядається як тверде тіло, що має поздовжню площину симетрії і двоточкову систему підвіски; неврівноваженість і гіроскопічні моменти обертових мас трансмісії і двигуна дорівнюють нулю; приводні колеса притискаються до вертикальної стінки монорейки з зусиллям, прямо пропорційним коефіцієнту жорсткості притискного механізму.
5.3 Побудова руху при заданих параметрах в системі Mathcad
При побудові математичної моделі були використані наступні початкові умови , наведені на рис 5.4.

Рисунок 5.4 – Початкові умови з прийнятими допущеннями.
Після підставляння початкових умов в тіло програми отримали наступні графіки, що відображають рух тіла по осях X,Y і зазначенням сили натягу виникає в частині кріплення складу рис. 4.5, а також X,Y,Z рис. 5.6.

Рисунок 5.5 Графічне відображення руху і виникає сили натягу.

Рисунок 5.6 Графічне відображення бокових відхилень.
Аналогічні розрахунки проведемо для початкового відхилення в діапазоні від 0 до 10 градусів і вагою 210 кг Сила F, яка виникає в системі підвішування екіпажу при збільшенні початкового відхилення екіпажу зменшується.

Висновки
На підставі проведеного аналізу рівняння розгойдування екіпажу при русі монорейкою можна зробити висновок, що існують періодичні за часом коливання точки підвісу, при яких відхилення екіпажу від заданого фіксованого нахиленого положення можуть бути скільки завгодно малими.
При написанні даного реферату магістерська робота не завершена. Остаточний варіант роботи можна отримати у автора або наукового керівника після грудня 2014 року.
Перелік посилань
- Айзеншток Л.И. Исследование динамики и обоснование параметров конструкции и условий эксплуатации шахтных скоростных монорельсовых дорог: Автореф. дис. Канд. тех. наук. – Днепропетровск, 1983. – 23 с.
- Айзеншток Л.И., Носов В.С., Слободенюк Р.Л. Исследование состояния пути шахтных монорельсовых дорог // Способы и средства безопасной эксплуатации электромеханического оборудования в шахтах. Сб. науч. тр. / МакНИИ. – 1982. – С. 61–62.
- Нос В.С., Айзеншток Л.И. О зазорах в выработках при монорельсовом транспорте // Безопасность труда в промышленности. Сб. науч. тр. / МакНИИ. – 1982. – №2. – С. 47–48.
- Шахтарь П.С. Рудничные составы. – М.: Недра, 1982. – 296 с.
- Фаворин М.В. Моменты инерции тел. – М.: Машиностроение, 1977. – 511 с.
- Капица П.Л. Динамическая устойчивость маятника при колеблющейся точке подвеса // Журн. эксперимент. и теор. физики. – 1951. – 51, № 5. – С. 588–597.
- Капица П.Л. Маятник с вибрирующим подвесом // Успехи физ. наук. – 1951. – 44. –С. 7–20.
- Stephenson A. On a new type of dynamic stability // Mem. and Proc. of the Manchester Literary and Philosophical Soc. – 1908. – 52, № 8. – P. 1–10.
- Stephenson A. On induced stability // Philosophical Magazine. – 1908. – 15. – P. 233–236.
- Стретт Дж.В. Теория звука. – М.: Гос. изд–во технико–теоретической лит., 1955. Т. 1.- 504 с.
- Боголюбов Н.Н. Теория возмущений в нелинейной механике // Сб. тр. Ин–та строител. механики АН УССР. – 1950. – 14. – С. 9–34.
- Крылов H.M., Боголюбов Н.Н. Введение в нелинейную механику. – Киев: Изд–во АН УССР, 1937. – 365 с.
- Боголюбов Н.Н. О некоторых статистических методах в математической физике. –Киев: Изд–во АН УССР, 1945. – 139 с.
- Erdelyi A. Uber die kleinen Schwingungen eines Pendels mit oszillierendem Aufhangepunkt // ZAMM. – 1934. – 14, № 4. – S. 235–247.
- Klotter K., Kotowski G. Uber die Stabilitat der Bewegungen des Pendels mit oszillierendem Aufhangeunkt // Ibid. – 1939. – 19, № 5. – S. 289–296.
- Hirsch P. Das Pendel mit oszilliererndem Aufhangepunkt // Ibi'd. – 1930. – 10, № 1. –S. 41–52.
- Жалким И.Г. Некоторые задачи теории нелинейных колебаний. – М.: Гостехиздат, 1956.- 491 с.
- Блехман И.И. Вибрационная механика. – М.: Наука, 1994. – 400 с.
- Стрижак Т.Г. Методы исследования динамических систем типа "маятник". – Алма– Ата: Наука, 1981. – 253 с.
- Бардин Б.С., Маркеев А.П. Об устойчивости равновесия маятника при вертикальных колебаниях точки подвеса // Прикл. математика и механика. – 1995. – 59, № 6. – С. 922–929.
- Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем.-СПб.: Изд–во С.-Петербург. ун–та, 2002. – 308 с.
- Сейранян А.А., Сейранян А.П. Об устойчивости перевернутого маятника с вибрирую¬щей точкой подвеса // Прикл. математика и механика. – 2006. – 70, № 5. – С. 835–843.
- Lowenstern E. R. The stabilizing effect of imposed oscillations of high frequency on a dynamical system // Philosoph. Magazine. – 1932. – 8. – P. 458–486.
- Hsu, C.S. On a restricted class of coupled Hill's equations and some applications //J.Appl. Mech. – 1961. – 28. – P. 551–556.
- Холостова О.В. О движениях двойного маятника с вибрирующей точкой подвеса // Изв. РАН. Механика твердого тела. – 2009. – № 2. – С. 25–40.
- Otterbein S. Stabilisierung des n–Pendels und der Indische Seiltrick // Arch. ration. Mech.Analysis – 1982. – 78. – P. 381–393.
- Acheson D.J. A pendulum theorem // Proc. R. Soc. Lond. – 1993. – A443 – P. 239–245.
- Маркеев А.П. О близких к коническим движениях сферического маятника с вибрирующей точкой подвеса // Тр. конф. «Устойчивость и колебания нелинейн. систем упр.». – 1998. – С. 107.
- Петров А.Г. Об уравнениях движения сферического маятника с колеблющейся точкой подвеса // Докл. РАН. – 2005. – 405, № 1. – С. 51–55.
- Маркеев А.П. К теории движения твердого тела с вибрирующим подвесом // Доклады Академии наук. 2009. Т. 427. № 6. С. 771–775.
- Холостова О.В. Исследование устойчивости перманентных вращений Штауде. М. –Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. – 128 с.
- SMT Scharf [Электронный ресурс] – Режим доступа: http://smtscharf.com/cms/front_content.php?lang=5&idcat=3. Дата обращения 05.11.2012.
