Кондрахин В.П., докт. техн. наук, проф., Мельник А.А.,

Донецкий национальный технический университет,

Косарев В.В., канд. техн. наук, Стадник Н.И., докт. техн.

наук, Косарев И.В., Донгипроуглемаш

В статье предложена математическая модель для исследования нагрузок в многодвигательном приводе и тяговом органе забойного скребкового конвейера с двухскоростными асинхронными электродвигателями.

The paper presents a mathematic model for studying the loads in a multimotor drive and drag-chain unit of an armored conveyor with double speed electric motors.

Проблема и ее связь с научными и практическими задачами.

Отличительной особенностью современных скребковых забойных конвейеров является использование для их привода двухскоростных асинхронные электродвигателей, не требующих применения гидродинамических муфт. Типичным примером таких машин являются разработанные институтом «Донгипроуглемаш» энерговооруженные (400-700 кВт) скребковые конвейеры типажного ряда КСД. Отсутствие ненадежной и сложной в обслуживании гидромуфты повышает эксплуатационные качества таких конвейеров, однако при этом возникают проблемы, связанные с работой многодвигательного привода в переходных режимах пуска и стопорения тягового органа.

Пусковые режимы многоприводных конвейеров предусматривают определенную последовательность включения электродвигателей головного и хвостового привода на первую и вторую скорость. В настоящее время эта последовательность установлена эмпирически и не учитывает особенности эксплуатации конвейера в конкретном очистном забое: длину лавы, угол и направление транспортирования, степень загрузки и др. Для оптимальной адаптации режима пуска конвейера к работе в заданных условиях необходимо создать математическую модель, которая позволит исследовать процесс формирования пусковых нагрузок в приводах и тяговом органе.

Анализ исследований и публикаций. Вопросам создания математических моделей скребковых конвейеров посвящены работы [1…5 и др.]. В них рассматривались приводы конвейеров с односкоростными электродвигателями и гидродинамическими муфтами. В работе [6] разработана математическая модель двухприводного двухскоростного скребкового конвейера, пригодная для оптимизации пусковых режимов подобных машин. Однако в ней тяговый орган с грузом представлен в виде одной сосредоточенной массы, что при моделировании работы конвейеров большой длины (300 м и более) может приводить к существенным погрешностям. Таким образом, известные математические модели не в полной мере пригодны для корректного исследования и оптимизации многоприводных скребковых забойных конвейеров с двухскоростными электродвигателями, работающих в длинных очистных забоях.

Постановка задачи. В работе поставлена и решена задача создания математической модели, пригодной для исследования нагрузок в многодвигательном приводе длинного (300 м и более) забойного скребкового конвейера в процессе его запуска на первую и вторую скорости.

Изложение материала и результаты. Для разработки математической модели конвейера использовано представление тягового органа с грузом в виде совокупности конечных элементов, обладающих упругими, диссипативными и инерционными свойствами [7]. При разработке расчетной схемы скребкового конвейера были приняты следующие основные допущения:

– тяговый орган представлен как совокупность конечных элементов, состоящих из массы m и линейной упруго-диссипативной связи (коэффициентами жесткости и сопротивления соответственно C_ц, ß_ц), работающей только на растяжение;

– корпуса редукторов привода конвейера и оси тяговых звездочек закреплены абсолютно жестко.

Расчетная схема для общего случая с произвольным количеством конечных элементов (n_p и n_х соответственно на рабочей (верхней) и холостой (нижней) ветвях тяговой цепи) приведена на рис. 1. Диссипативные элементы располагаются параллельно с упругими и на схеме условно не показаны. Все элементы приведены к роторам приводных двигателей. На схеме приняты следующие обозначения:

Рисунок 1 – Динамическая схема трехприводного скребкового забойного конвейера

J_д –момент инерции роторов электродвигателей;

M_д1, M_д2, M_д3– электромагнитные моменты 1-го, 2-го и 3-го электро-

двигателей;        

J_зв –момент инерции приводной звезды;

С_п – коэффициент жесткости редуктора привода;

m_г – масса груза, соответствующая одному конечному элементу ;

F_c – сила сопротивления движению массы m участка тяговой цепи и

груза (с учетом составляющей веса mg·sinα при работе на пласте с углом падения α) .

В качестве обобщенных координат для математического описания системы приняты:

φ_д1, φ_д2, φ_д3 – углы поворота роторов электродвигателей;

φ_з1, φ_з2 – углы поворота приводных звезд;

x_pi, x_xi – координата i – ой массы конечных элементов – аналогов

тяговой цепи на рабочей и холостой ветвях [7].

Как видно на рис. 1, первые по порядку массы конечных элементов на рабочей и холостой ветвях условно присоединены к соответствующим приводным звездам, т.е. x_p1 = Rз φ_з1 и x_х1 = - R_з φ_з2.

На каждую массу в направлении перемещения действуют реакции линейных упруго-демпфирующих связей, составляющая силы веса и внешняя сила сопротивления перемещению.

Для исследования процесса запуска конвейера необходимо выполнить корректное математическое описание силы сопротивления F_c, действующей на i-ю массу в процессе ее страгивания с места при пуске конвейера и в движении. Известно [1], что сила сопротивления движению тягового органа и груза зависит от скорости. Для покоящейся i–ой массы (т.е. при x_i = 0 ) принимаем:

F _c = F_пi, где

F_пi = F_уд(i−1) − F_удi ; при F_уд(i−1) − F_удi < F_двi (0);

F_пi = F_двi (0); при F_уд(i−1) − F_удi ≥ F_двi (0),

где – реакция в соответствующем участке тягового органа;

 – для холостой ветви;

 – для незагруженной части рабочей ветви;

 - для загруженной части рабочей ветви;

 – обобщенные коэффициенты сопротивления перемещению, соответственно, на порожней и груженой ветвях (принимаются в соответствии с рекомендациями работы [1]); эти зависимости в общем случае удобно представить в виде полиномов третьей степени).

α –  угол транспортирования груза.

Верхний знак соответствует транспортированию груза снизу-вверх, нижний – сверху–вниз.

После страгивания i-ой массы с места (т.е. при x_i ≠ 0 ) принимаем F_c=F_дві.

Для составления системы дифференциальных уравнений, описывающих движение механической системы скребкового конвейера, используем уравнения Лагранжа II рода. Этот метод составления уравнений движения является в данном случае наиболее удобным, поскольку позволяет формализовать расстановку знаков реакций связей в узловых точках (на приводных звездах), где кинематические цепи разветвляются.

Система дифференциальных уравнений, описывающая динамические процессы в трехприводном скребковом конвейере, полученная на основе уравнений Лагранжа II рода, имеет вид (1), где

R_з – средний радиус приводной звезды;

β_п – коэффициент сопротивления редуктора .

Величина массы m конечного элемента опредляется принятым количеством элементов, а также наличием или отсутствием груза на рассматриваемом участке цепи: m = mц + mг - если груз имеется, и

m = mц - для незагруженного участка ( mц , mг – массы, соответствен но, цепи и груза, относящиеся к рассматриваемому конечному элементу).

В предложенной модели использовано математическое описание электромагнитных процессов в двухскоростных асинхронных двигателях, приведенное в работе [6].

Адекватность разработанной модели реальной системе установлена путем сравнения результатов моделирования и экспериментальных стендовых исследований трехприводного конвейера КСД27 длиной 82 м. Погрешность в определении крутящих моментов приводов и частоты вращения электродвигателей при пуске в большинстве случаев не превышает 20 %.

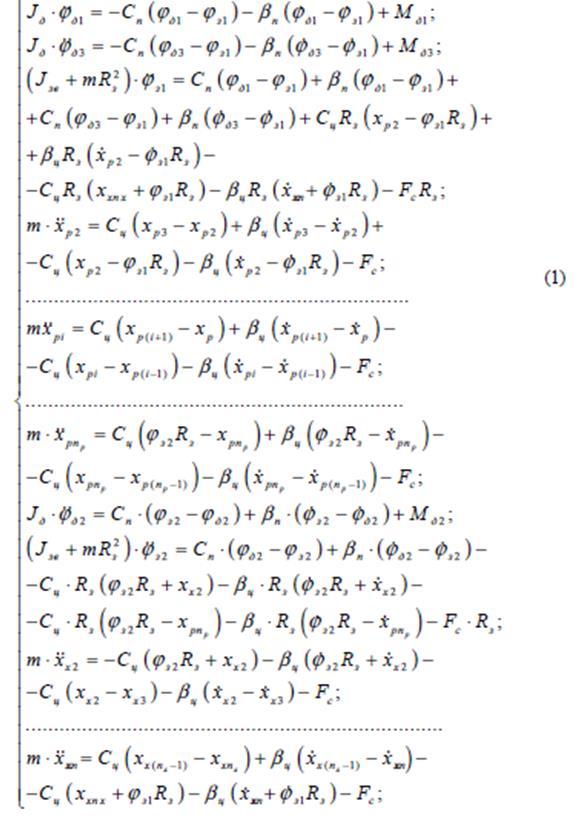
Важную роль в формировании динамических процессов при пуске забойного скребкового конвейера играет образовавшаяся в результате вытяжки и износа слабина цепи в точках сбегания с приводных звездочек. Для учета слабины цепи в точке сбегания с головного привода Δl_ц в математической модели предусматривается при определении координат точек набегания и сбегания цепи на звездочке хвостового привода увеличение этих координат на величину 0,5Δl_цu, где u – передаточное отношение редуктора. Умножение на u обеспечивает приведение величины смещения к ротору электродвигателя, к которому приведены все параметры модели. Увеличение координат точек набегания и сбегания на указанную величину в реальном конвейере соответствует смещению хвостового привода в сторону головного на величину 0,5Δl_ц. Начальные условия при интегрировании уравнений движения принимаются следующим образом:

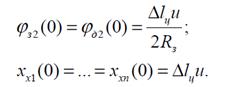
Остальные начальные условия принимаются нулевыми.

На базе системы уравнений (1) выполнено моделирование процессов пуска, работы под нагрузкой и внезапного стопорения тягового органа забойного скребкового конвейера КСД27. В качестве примера принят конвейер длиной 315 м, транспортирующий горную массу вниз под углом 13º. Эти достаточно представительные условия соответствуют работе скребкового конвейера КСД27 на шахте 1/3 «Новогродовская». Погонная масса груза на полотне конвейера принималась 90 кг/м, что соответствует производительности примерно 6 т/мин.

В качестве базового для трехприводных конвейеров на практике используется следующий алгоритма пуска:

– запуск хвостового электродвигателя на низкую скорость (НС), через Δt₁=1,5 с запуск обоих головных на НС;

– через 6 с запуск хвостового электродвигателя на высокую ско-

рость (ВС), затем через интервал времени Δt₂ = 0,25 с - запуск обоих головных двигателя на ВС.

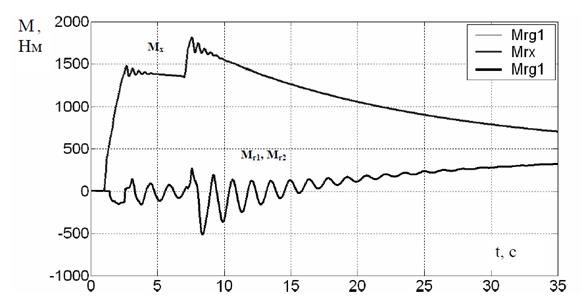
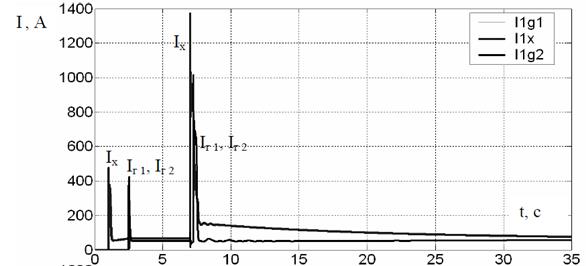
Осциллограммы процесса пуска загруженного на всю длину трехприводного конвейера приведены на рис. 2. На рисунке приняты обозначения: Мх, Мг1,Мг2–приведенные к электродвигателю моменты

в редукторе, соответственно, хвостового и двух головных приводов;

Рисунок 2. – Полученные при моделировании осциллограммы про-

цесса пуска по базовому алгоритму загруженного на всю длину трех-

приводного конвейера КСД27 длиной 315 м

I_х , I_г1, I_г2 – токи электродвигателей хвостового и головных приводов;

n_х , n_г1, n_г2 – частоты вращения роторов электродвигателей хвостового и головных приводов. Поскольку запуск обоих головных приводов происходит одновременно, все величины, относящиеся к этим приводам, изменяются синхронно. На осциллограмме видно, что запуск производится в основном под действием хвостового привода, оба головных электродвигателя практически не нагружены и в запуске практически не участвуют. Процесс выравнивания нагрузки между приводами занимает достаточно продолжительный период времени (свыше 40 с). Приведенный пример показывает, что принятый в настоящее время алгоритм запуска в данных условиях работы конвейера не является оптимальным и требует усовершенствования.

Выводы и направление дальнейших исследований. Разработанные математические модели многоприводных скребковых конвейеров с двухскоростным приводами впервые комплексно учитывают следующие факторы: электромагнитные переходные процессы в приводных электродвигателях; распределение динамических свойств тягового органа и груза вдоль его длины; характер изменения момента сил сопротивления в процессе запуска; наличие слабины тягового органа в точках сбегания с приводных звезд. На основе разработанных математических моделей будет решена задача оптимизации режимов запуска многоприводных конвейеров с двухскоростными электродвигателями для заданных условий эксплуатации.

Список источников.

1. Чугреев Л.И. Динамика конвейеров с цепным тяговым органом.- М.: Недра, 1976.- 256с.

2. Скребковые конвейеры. Справочник / Под ред. А.В. Леусенко. - М.: Недра, 1992. – 221с

3. Алгоритмы расчетов шахтных скребковых конвейеров / Коренев С.В., Косарев И.В., М.В. Плетнев, Н.И. Стадник, Л.Н. Ширин .- Луганск, Книжковий світ, 2006,- 94 с.

4. Осичев А.В., Ткаченко А.А. Разработка семейства компьютерных моделей для исследования динамических процессов в электроприводах скребковых конвейеров. Вісник КДПУ імені Михайла Остроградського.- Кременчук: КДПУ, 2008.- Вип. 3/2008 (50).- частина 2.-С. 154-157.

5. David H. Wauge. Modeling of an Armored Face Conveyor. Department of Mechanical Engineering. University of Queensland. Masters of Engineering Science Thesis August 19, 2002.

6. Кондрахин В.П., Борисенко В.Ф., Мельник А.А., Косарев В.В., Стадник Н.И., Косарев И.В. Моделирование пусковых режимов скребкового конвейера типа КСД // Наукові праці Донецького національного технічного університету, вип.13(123), Серія: гірничоелектромеханічна.- Донецьк: ДонНТУ.- 2007.- C.64-73.

7. Обоснование конечно-элементной модели тягового органа скребкового конвейера // Кондрахин В.П., Борисенко В.Ф., Мельник А.А. и др.- Наукові праці Донецького національного технічного університету, вип. 99 , Серія: гірничо-електромеханічна.- Донецьк: ДонНТУ.-2005.- С.97-103.

Дата поступления статьи в редакцию: 31.10.08