Рубель Л.А., Горбовский И.В. - Исследование линеаризованной модели автоматизированного вынесенного привода подачи с электромагнитным тормозом скольжения для горных машин

Вынесенная система подачи (ВСП) с электромагнитной муфтой скольжения (ЭМС) достаточно успешно применяется для перемещения комбайнов для тонких пластов в лавах длиной до 200 м уже более 30 лет. Однако при современных технологиях выемки тонких пластов с увеличением длин лав до 300 м появилась необходимость существенного увеличения мощности приводов ВСП. Одним из решений этой проблемы явилось создание привода, в котором в качестве вариатора скорости используется электромагнитный тормоз (ЭМТ). Это позволило помимо увеличения мощности получить ряд преимуществ, улучшающих охлаждение, параметры надежности и уменьшение габаритов привода. С точки зрения управления приводом, существенно увеличилась его электромагнитная и механическая инерционность. С другой стороны, существенно уменьшилась зависимость индуктивности обмотки возбуждения ЭМТ от тока управления из-за уменьшения степени насыщения магнитопровода в рабочем диапазоне токов. Изменение так же претерпели и механические характеристики привода (рис.1).

Рисунок 1 – Семейство механических характеристик ЭМТ.

Принципиальной особенностью привода с ЭМТ является необходимость системы стабилизации скорости, обеспечивающей требуемую форму механических характеристик. Поэтому, указанные конструктивные изменения потребовали уточнения математической модели привода, необходимой для разработки системы автоматического управления скоростью подачи.

На основании результатов экспериментальных исследований разработана математическая модель собственно привода подачи с ЭМТ [1]. В модели учтены реальные статические и динамические характеристики привода, а также специфика нового дискретного датчика скорости вращения приводной звезды.

Структурная схема автоматизированного привода представлена на рис. 2. Штриховой линией выделена часть модели, представляющая собственно модель привода с ЭМТ. Модель реализована и исследована в среде SIMULINK.

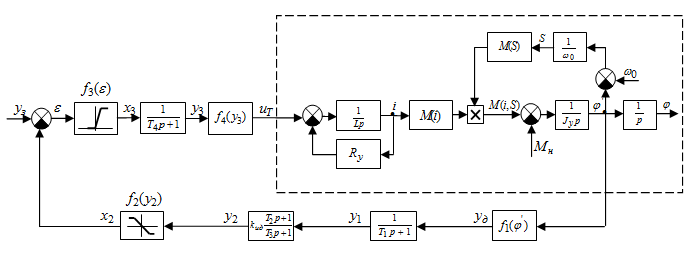
Рисунок 2 – Структурная схема привода с ЭМТ.

Соответствующая структурной схеме система дифференциальных уравнений имеет вид:

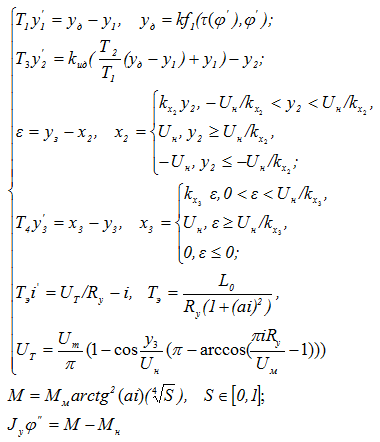
где T₁–T₄ – постоянные времени соответствующих динамических звеньев; T_э – временная характеристика обмотки управления ЭМТ; y_д – выходной сигнал дискретного датчика скорости с коэффициентом преобразования k и временем запаздывания тау; фи – угол поворота приводной звезды; k_ид – коэффициент усиления интегро-дифференцирующего звена; E – сигнал рассогласования; k_x2, k_x3, x₂, x₃ – коэффициенты усиления и выходные сигналы соответствующих нелинейных звеньев; U_н – напряжение ограничения выходного сигнала нелинейных звеньев; U_т – выходное напряжение тиристорного преобразователя; R_y – активное сопротивление обмотки управления ЭМТ; i – ток управления ЭМТ; U_m – амплитуда синусоидального напряжения питания тиристорного преобразователя; M – электромагнитный момент ЭМТ; M_k – критический момент ЭМТ; a – эмпирический коэффициент, учитывающий степень насыщения магнитопровода ЭМТ; J_y – момент инерции вращающихся элементов привода, приведенный к приводной звезде; S – скольжение ЭМТ; M_н – момент нагрузки, приложенный к звезде привода.

На основании математической модели разработана структура и выполнен параметрический синтез системы стабилизации и управления скоростью подачи комбайна [2].

Приведенная структура и математическая модель показывают, что привод с системой стабилизации скорости является существенно нелинейной динамической системой высокого порядка. Это делает крайне затруднительным аналитический синтез структуры и параметров системы автоматического управления скоростью привода. В связи с этим поставлена задача проверить возможность использования линеаризованной модели для структурного и параметрического синтеза САУ скоростью привода.

Для решения поставленной задачи выполним линеаризацию нелинейных элементов схемы. Так электромагнитный момент ЭМТ М, математическая формула которого приведена выше, содержит две нелинейные функции. Напряжение на выходе тиристорного преобразователя также содержит две нелинейных функции.

Для линеаризации этих зависимостей применим разложение в ряд Тейлора:

где M(1,0.6) – электромагнитный момент при токе равном 1 А и соответствующем скольжении 0.6. Данная точка на механических характеристиках была выбрана исходя из линейного участка на кривой. Аналогично применим разложение в ряд Тейлора U_т.

Подставим полученные линейные функции в исходную модель. Результаты исследований качества переходных процессов изменения угловой скорости привода w (регулируемый параметр) и тока в обмотке управления ЭМТ приведены на рисунке 3.

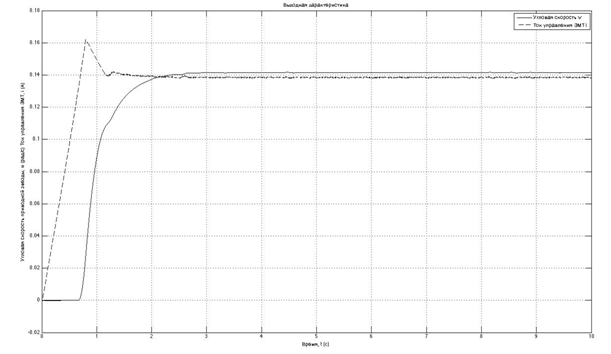
Рисунок 3 – Переходный процесс изменения угловой скорости и тока в обмотке управления ЭМТ для линеаризованной модели привода.

На рис. 4 показан приведенный переходный процесс для нелинейной модели привода.

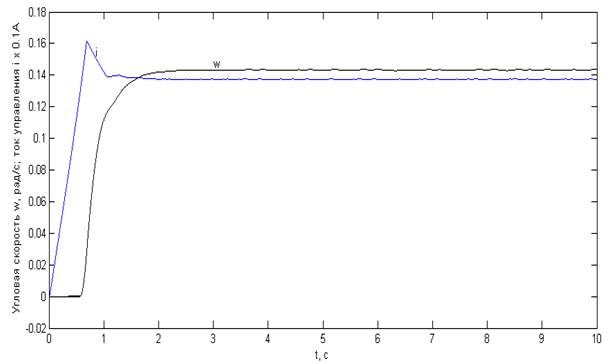
Рисунок 4 – Переходный процесс изменения угловой скорости и тока в обмотке управления ЭМТ для нелинейной модели привода.

Полученные характеристики показали небольшие различия линеаризованной и нелинейной моделей как для управляющего воздействия – тока управления, так и для регулируемого параметра – угловой скорости привода. Это делает возможным применение линейных методов теории автоматического управления для разработки системы управления скоростью привода и применению стандартных регуляторов.

Выводы

1. Исследованы динамические характеристики и качество переходных процессов нелинейной модели автоматизированного привода подачи с ЭМТ.

2. Разработана линеаризованная модель автоматизированного вынесенного привода подачи с ЭМТ, исследованы его динамические характеристики и качество переходных процессов .

3. Сравнение нелинейной и линеаризованной моделей позволяет использовать линейные методы структурного и параметрического синтеза системы стабилизации скорости привода.

Исследование линеаризованной модели автоматизированного вынесенного привода подачи с электромагнитным тормозом скольжения для горных машин

Выводы

Перечень ссылок