УДК 533.6.08
Кузнецов Д. Н., канд. техн. наук,
Чупис Д. А.
Источник: Кузнецов Д. Н.,
Чупис Д. А.. Моделирование метрологических
характеристик различных типов
термоанемометров с термистором
в качестве чувствительного элемента /
Электротехнические и компьютерные системы. Научно-технический журнал
№ 06 (82). Одесский национальный политехнический
университет.
— Киев: Техника
,
2012. —
С. 99-105.
МОДЕЛИРОВАНИЕ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК РАЗЛИЧНЫХ ТИПОВ ТЕРМОАНЕМОМЕТРОВ С ТЕРМИСТОРОМ В КАЧЕСТВЕ ТЕРМОЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА
Разработаны
математические модели и выполнено моделирование основных
метрологических характеристик термоанемометров постоянных температуры,
тока и мощности с термистором в качестве термочувствительного элемента.
Выделены особенности различных типов термоанемометров, даны
рекомендации по их практическому использованию.
Ключевые
слова:
термоанемометр, математическая модель, метрологические характеристики.
PhD. Kuznetsov D. N., ,
Chupis D. A.
METROLOGICAL CHARACTERISTICS SIMULATION FOR THE DIFFERENT TYPES OF THE HEAT-LOSS ANEMOMETERS WITH THE THERMISTOR AS A SENSITIVE ELEMENT
Mathematical
models were designed and simulation of the main metrological
characteristics for the constant temperature, constant current and
constant power heat-loss anemometers with the thermistor as a sensitive
element was carried out in present paper. Special features of different
heat-loss anemometer types were highlighted and recommendations for its
practical use were presented.
Keywords:
heat-loss anemometer, mathematical model, metrological characteristics.
Кузнєцов Д. М. ,
канд.
техн.
наук,
Чупіс Д. А.
МОДЕЛЮВАННЯ МЕТРОЛОГІЧНИХ ХАРАКТЕРИСТИК РІЗНОМАНІТНИХ ТИПІВ ТЕРМОАНЕМОМЕТРІВ З ТЕРМІСТОРОМ В ЯКОСТІ ТЕРМОЧУТЛИВОГО ЕЛЕМЕНТА
Розроблено
математичні моделі та виконано моделювання основних метрологічних
характеристик термоанемометрів постійних температури, струму та
потужності з термістором як термочутливим елементом. Виділено
особливості різних типів термоанемометров, дані рекомендації щодо їх
практичногоь використання.
Ключові слова:
термоанемометр, математична модель, метрологічні характеристики.
Актуальность.
Термоанемометрический метод относится к числу косвенных методов
измерения скорости движения жидкостей и газов. Он основан на
зависимости теплоотдачи нагретого термочувствительного
элемента (ТЧЭ)
от скорости течения потока, физических свойств газа (теплопроводности и
вязкости) и разности температур ТЧЭ и газа. Охлаждение ТЧЭ потоком газа
приводит к уменьшению его температуры, изменению электрического
сопротивления и Джоулева тепловыделения. Измеряя падение напряжения на
ТЧЭ и ток в его цепи, можно, при известных физических свойствах
материала чувствительного элемента и закономерностях теплообмена,
определить локальную скорость потока.
В зависимости от теплового режима ТЧЭ
различают термоанемометры постоянной температуры, термоанемометры
постоянного тока, термоанемометры постоянной мощности и импульсные
термоанемометры.
Одной из основных метрологической
характеристикой ТА является чувствительность S, численно равная
производной выходного напряжения ЧЭ термоанемометра U
по скорости потока v:
Чем выше чувствительность, тем
большую точность измерений способен обеспечить термоанемометр при
прочих равных условиях. Известно, что чувствительность термоанемометров
с датчиками из металла тем выше, чем больше перегрев ТЧЭ. Однако данное
утверждение не распространяется на термоанемометры с термисторными
ТЧЭ [1]. Это объясняется отрицательным
экспоненциальным температурным
коэффициентом (ТКС) термистора, в отличие от положительного
квазилинейного ТКС металлов. Таким образом, возникла задача определения
оптимальных тепловых режимов термисторных термоанемометров, при которых
достигается максимальная чувствительность. Поставленная задача решена
путем математического моделирования характеристик различных типов
термоанемометров.
Основными задачами
математического моделирования термоанемометров являются:
1) Оценка
влияния режима работы (тока, температуры
перегрева, мощности) на чувствительность различных типов ТА.
2) Определение оптимальных режимов работы ТА, при
которых
обеспечивается максимальная чувствительность по скорости.
3) Оценка основных метрологических характеристик:
динамического диапазона измерений и чувствительности различных типов ТА
при оптимальных режимах работы.
4) Проведение сравнительного анализа
результатов моделирования.
Рассмотрим полученные результаты математического моделирования и исследований ТА постоянной температуры, постоянных тока и мощности с миниатюрным термистором в качестве ТЧЭ. Моделирование выполнялось для температуры потока 25 ºС в диапазоне скоростей потока v от 1 до 25 м/с. Экспериментально определено, что коэффициент рассеяния ЧЭ H в выбранном диапазоне скоростей для выбранного термистора изменяется от 0,1 до 0,5 мВт/ºС.
Моделирование ТА постоянной температуры. Исследуем влияние температуры перегрева ∆ TЧЭ на чувствительность термоанемометра постоянной температуры. Известно, что коэффициент рассеяния определяется как количество теплоты, отдаваемое ТЧЭ в единицу времени при разности температур между поверхностью и воздушным потоком, равной одному градусу [2]:
где Р1 — рассеиваемая ТЧЭ мощность, Тw и Тg — температура ЧЭ и газа соответственно. В установившемся режиме работы термоанемометра рассеиваемая в потоке мощность Р1 равна подводимой к ТЧЭ мощности Р2:
где U —
напряжение,
приложенное к ЧЭ, Rt — сопротивление ЧЭ.
Подставим выражение Р1 из (3) в (2), запишем относительно напряжения,
получим
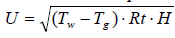 (4)
(4)
Из (4) следует, что
полезный сигнал термоанемометра зависит от температуры перегрева,
сопротивления ТЧЭ и коэффициента рассеяния, который, в свою очередь,
зависит от скорости потока газа. Последняя зависимость лежит в основе
работы термоанемометра.
Определим чувствительность
термоанемометра по скорости:
 (5)
(5)
Из полученного выражения следует, что чувствительность термоанемометра
тем выше, чем больше произведение перегрева на сопротивление ЧЭ (Tw
– Tg)•Rt.
Очевидно, что в случае применения в
качестве ТЧЭ термоанемометра проволочного или пленочного датчика из
металла (вольфрам, платина и др.), чувствительность термоанемометра
будет тем выше, чем больше перегрев ТЧЭ. Это объясняется тем, что
металлы имеют положительный температурный коэффициент сопротивления
(ТКС).
Неоднозначность появляется в случае
применения в качестве ТЧЭ термистора, так как термистор имеет
отрицательный ТКС и с увеличением температуры его сопротивление
уменьшается по экспоненциальному закону
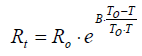 (6)
(6)
где Rt —
сопротивление термистора при
температуре Т; R0 —
сопротивление термистора при температуре Т0.
Зависимости коэффициента чувствительности
термоанемометра от температуры ТЧЭ при температурах воздуха 15 и
35 ºС
(стандартный диапазон для жилых помещений), полученные для термистора с
параметрами R0 = 5000 Ом и
B = 3500 K, приведены на рис. 1.
Из результатов следует, что существуют
оптимальные температуры термистора, при которых чувствительность ТА
максимальна. Например при температуре воздушного потока 15 ºС
оптимальной является температура термистора порядка 46 ºС,
а при Tg = 35 ºС
— порядка 70 ºС.
Ниже представлены результаты расчета
оптимальной температуры ТЧЭ (рис. 2) и оптимальной температуры
перегрева (рис. 3) для различных температур газа.
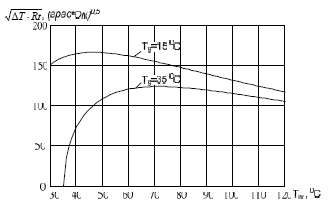
Рис. 1 — Зависимость коэффициента чувствительности термоанемометра от температуры ЧЭ Tw при 15 и 35 ºС температуре газа Tg
Из результатов моделирования следует, что при использовании ТА
постоянной температуры в широком диапазоне рабочих температур
измеряемых потоков оптимальная температура разогрева Tw термисторного
ТЧЭ также изменяется в достаточно широких пределах. Например, при
изменении температуры потока от 0 до 50 ºС
оптимальная температура разогрева термистора изменяется в пределах от
28 до 90 ºС.
Анализ результатов показывает, что
наиболее критичным для ТА постоянной температуры является режим, при
котором температура газа максимальна, так как с ростом температуры
потока чувствительность ТА падает.
Таким образом, обоснованной следует
считать рекомендацию по выбору оптимальной температуры термистора ТА
постоянной температуры именно для максимальной рабочей температуре
газа. В рассматриваемом случае в рабочем диапазоне температур газа от
от 0 до 50 ºС
оптимальной является температура
термистора 90 ºС.

Рис.2 — Зависимость оптимальной температуры ТЧЭ от температуры газа

Рис. 3 — Зависимость оптимальной температуры перегрева ТЧЭ от температуры газа
Ниже приведены результаты моделирования чувствительности ТА постоянной
температуры (рис. 4 и 5), полученные для температуры газа
Tg = 20 ºС
при различных перегревах и коэффициентах рассеяния термистора. По
результатам моделирования выполним оценку основных метрологических
характеристик ТА постоянной температуры. При температуре газа
Tg = 20 ºС
и оптимальном перегреве dT = 30 ºС
установлены:
– диапазон выходных напряжений ТА, В
от 1,4 до 3,2
– минимальная
чувствительность, В· ºС / мВт
3200
– максимальная чувствительность, В· ºС
/мВт
7200
– максимальная температура термистора
Twmax 50
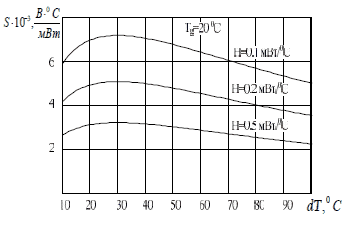
Рис. 4 —
Зависимость
чувствительности по скорости ТА постоянной температуры от перегрева
термистора при различных коэффициентах рассеяния термистора
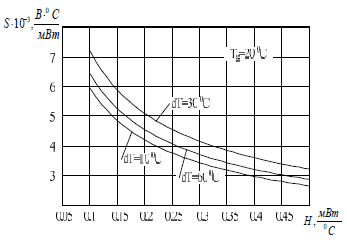
Рис. 5 — Зависимость чувствительности по скорости ТА постоянной температуры от коэффициента рассеяния термистора при различных перегревах термистора
Моделирование ТА постоянного тока. Исследуем влияние тока, протекающего через термисторный ЧЭ, на чувствительность термоанемометра постоянного тока. Распишем коэффициент рассеяния:
где I и
Rt —
соответственно ток и сопротивление
термистора;
dT = Tw - Tg —
перегрев термистора.
Из (7) сопротивление термистора
Так как сопротивление термистора является функцией перегрева, то
 (9)
(9)
Приравняв (8) и (9), получим базовое уравнение для моделирования ТА постоянного тока с термистором в качестве ТЧЭ
 .
(10)
.
(10)
Уравнение (10) позволяет определять перегрев термистора dT при различных значениях тока I и коэффициента рассеяния H. По известному перегреву несложно рассчитать напряжение на ТЧЭ
Для оценки чувствительности ТА по скорости использовалось выражение
Результаты моделирования
зависимости чувствительности S ТА постоянного тока от тока через
термистор при трех различных коэффициентах рассеяния представлены на
рис. 6.
Из результатов следует, что для ТА постоянного тока при
заданном коэффициенте рассеяния (скорости потока) существует
оптимальное значения рабочего тока через ТЧЭ, при котором
чувствительность ТА будет максимальной.
Однако с ростом коэффициента рассеяния оптимальный
ток также растет. Например, при минимальной скорости потока
v = 1
м/с коэффициент рассеяния
H = 0,1 мВт/ºС
и оптимальный ток Iопт = 4 мА, а при
максимальной
скорости потока v = 25 м/с
и коэффициенте рассеяния H = 0,5 мВт/ºС,
оптимальным уже будет ток Iопт = 10 мА.
Так как с ростом коэффициента рассеяния
чувствительность ТА падает, то в качестве обоснованной рекомендации по
выбору оптимального рабочего тока через термистор ТА постоянного тока
следует считать выбор оптимального тока для максимального коэффициента
рассеяния. В рассматриваемом случае оптимальным является ток термистора
10 мА.

Рис. 6 — Зависимость чувствительности ТА постоянного тока от значения тока через термистор при различных коэффициентах рассеяния

Рис.= 7 — Зависимость чувствительности ТА постоянного тока от коэффициента рассеяния при различных значениях тока термистора
На рис. 7 приведены
результаты
моделирования зависимости чувствительности ТА постоянного тока от
коэффициента рассеяния при трех различных значениях тока термистора. Из
результатов следует, что при токе через термистор
10 мА
действительно
обеспечивается лучшая чувствительность при больших коэффициентах
рассеяния (на больших скоростях потока). По результатам моделирования
выполним оценку основных метрологических характеристик ТА постоянного
тока при температуре газа Tg = 20 ºС
и оптимальном токе через термистор
I = 10 мА, получены следующие
характеристики:
– диапазон выходных напряжений ТА, В
от 1,0 до 2,9
– минимальная
чувствительность, В· ºС
/мВт
3600
– максимальная чувствительность, В· ºС
/мВт
6900
– максимальная температура термистора Tw
max
120
Моделирование
ТА постоянной мощности.
Исследуем влияние мощности, выделяемой на термисторе ТА, на
чувствительность термоанемометра постоянной мощности. Получим базовые
уравнения, описывающие работу ТА в режиме постоянной мощности.
Перегрев термистора
где P —
мощность,
подводимая к термистору и рассеиваемая в потоке; Н —
коэффициент рассеяния термистора.
Сопротивление термистора как функция его
 (14)
(14)
Ток и напряжение термистора как функции мощности и коэффициента
рассеяния:
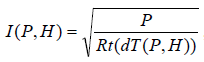 (15)
(15)
Результаты моделирования
зависимости чувствительности по скорости S ТА постоянной мощности от
мощности, рассеиваемой термистором, при трех различных коэффициентах
рассеяния представлены на рис. 8.
Из результатов следует, что для ТА
постоянной мощности оптимальное значение мощности, подводимой к
термистору, увеличивается с ростом коэффициента рассеяния. Например,
при минимальной скорости потока v = 1 м/с
коэффициент рассеяния H = 0,1 мВт/ºС
и оптимальная мощность Ропт = 9 мВт. Однако
при H ≥
0,2 мВт/ºС
оптимальное значение мощности, подводимой к термистору, становиться
больше 15 мВт, что может привести к чрезмерному перегреву термистора на
малых скоростях потока.
Таким образом, с одной стороны для повышения
чувствительности ТА постоянной мощности необходимо увеличивать
рассеваемую термистором мощность, а с другой
— следить, чтобы
на малых скоростях потока термистор не перегревался бы сверх
допустимого значения. В рассматриваемом случае оптимальной является
рассеиваемая термистором мощность 15 мВт.
На рис. 9 приведены результаты
моделирования
зависимости чувствительности ТА постоянной мощности от коэффициента
рассеяния при трех различных значениях мощности, рассеиваемой
термистором. Из результатов следует, что при мощности термистора
15 мВт
действительно обеспечивается лучшая чувствительность при больших
коэффициентах рассеяния (на больших скоростях потока).
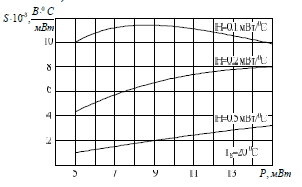
Рис. 8 — Зависимость чувствительности ТА постоянной мощности от значения мощности, подводимой к термистору, при различных коэффициентах рассеяния
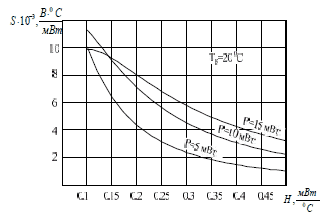
Рис. 9 — Зависимость чувствительности ТА постоянной мощности от коэффициента рассеяния при различных значениях мощности, подводимой к термистору
По результатам моделирования выполним оценку
основных метрологических характеристик ТА постоянной мощности при
температуре газа Tg = 20 ºС
и оптимальной мощности Р = 15 мВт, получим
– диапазон выходных напряжений ТА, В
от
0,75
до 3,2
– минимальная чувствительность Smin, В·ºС/мВт
3200
– максимальная чувствительность Smax, В·ºС
/мВт
9900
– максимальная температура термистора Tw max
170
Анализ
результатов моделирования.
В таблице приведены результаты оценки метрологических характеристик
различных типов ТА при оптимальных режимах работы, полученные путем
математического моделирования. Характеристики получены для температуры
газа Tg = 20 ºС
в диапазоне изменения коэффициента рассеяния Н от 0,1 до
0,5 мВт/ºС,
что соответствует скорости потока vот
1 до 25 м/с.
Сводная таблица результатов моделирования метрологических характеристик различных типов ТА
|
Параметр |
Режим
(тип ТА) |
||
|
Tw = const |
I = const |
P = const |
|
|
Диапазон
U, B |
|
|
|
|
Smin, B˚C/мВт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tw = 50
ºС |
I = 10 мА |
|
На основании анализа
результатов отметим следующие особенности различных типов
термоанемометров: В ТА постоянной температуры
(Тw = const) термистор
испытывает минимальные тепловые нагрузки
(Tw = 50 ºС),
что повышает стабильность его функции преобразования во времени и
надежность в целом. Максимальные тепловые нагрузки
(Tw max = 170 ºС)
характерны для режима постоянной мощности
(P = const).
На больших скоростях потока
чувствительность ТА постоянного тока несколько выше (на
10–12 %),
чем у ТА постоянной температуры и мощности.
На малых скоростях потока
чувствительность ТА постоянной мощности значительно выше (на
30 %), чем
у ТА постоянной температуры и постоянного тока.
ТА постоянной мощности имеет наибольший
диапазон выходного напряжения (от 0,75 до 3,2 В), что
обеспечивает
большую точность измерений при прочих равных условиях.
Выводы.
Таким образом, разработанные математические модели ТА постоянной
температуры, постоянного тока и постоянной мощности с термистором в
качестве ТЧЭ позволили:
1) оценить основные метрологические характеристики различных типов ТА;
2) определить оптимальные режимы их работы, при которых обеспечивается
максимальная чувствительность по скорости;
3) выполнить сравнительный анализ результатов моделирования и выделить
особенности различных типов ТА.
Список использованной литературы
1. Михеев М. А. Основы теплопередачи / Михеев М. А. , Михеева И. М.. — М.: Энергия, 1977. — 344 с.
2. Украинский Ю. Д. Определение и обеспечение оптимальных тепловых режимов термисторных термоанемометров постоянной температуры / Украинский Ю. Д., Кузнецов Д. Н., Балюра Д. Е.// Зб.наук.пр. ДонНТУ. Серія: Обчислювальна техніка та автоматизація. — 2007. — Вип. 12 (118). — c. 177-182.