Моделирование расхода воздуха в глубоких шахтах: применение в горной вентиляции.

Аннотация

Витрант Е., Джонсон К.Х., Моделирование расхода воздуха в глубоких шахтах: применение в горной вентиляции. В этой статье, мы представляем новый способ моделирования воздушного потока глубоких скважин, которая подходит для контроля в реальном времени крупномасштабных систем. Мы рассматриваем добывающее заявление контроля за вентиляцией, где специально предназначенные модели крайне важны для новых способов автоматизации, основанных на глобальном системном контроле и оптимизации потребления энергии. Предложены два разных уровня сложности. Начиная с общей модели, основанной на уравнении Навье-Стокса, мы получаем 0-D, модель Bond Graph. Эта модель используется для того, чтобы установить симулятор в реальном времени для решения проблемы аэрологии шахты.

Введение

Традиционно, контроль крупномасштабных систем, таких как вентиляция, было выполнено в местном масштабе с децентрализованными действиями контроля. Контроль за условиями и оптимизация следовательно относятся к предварительному дизайну глобальной системы и устройств автоматизации. Горная промышленность вентиляции предусматривает интересный пример развития автоматизации для крупномасштабных систем. После короткого библиографического расследования, без любых сложностей, мы можем отследить математические усилия по моделированию назад до 1968, где установившаяся разделенная на отсеки модель была предложена для сетей потока со сложной топологией[1]. В 1973 новые результаты на экспериментальном определении бурных коэффициентов распространения были представлены[2], указывая на мотивацию для более продвинутых моделей. Мы должны ждать, чтобы найти первое использование уравнения Навье-Стокса с упрощенным, подобным палате[3] и основной выработке [4] модели. О связанных проблемах нелинейности и нестационарного поведения, высокой размерности и числовых проблем быстро сообщили [5]. Этот короткий исторический обзор также иллюстрирует параллельное развитие магнитной способности моделирования и вычисления вентиляции. Горные инженеры были прежде всего обеспокоены надлежащим дизайном тоннелей вентиляции, вентиляторов и турбин, и более широко краткосрочного и долгосрочного планирования требований вентиляции[6]. Недавние технические разработки, в областях вложенного контроля и возможностей ощущения радио, мотивируют некоторые новые научно-исследовательские работы, ища глобальные стратегии автоматизации, которые допускали бы оптимизированный контроль в реальном времени системы вентиляции. Новое социополитическое беспокойство о потреблении энергии и увеличении цен на электроэнергию в контексте международных соревнований также мотивирует теоретическое исследование, приводящее к улучшенным алгоритмам контроля. В этой газете мы решаем проблему определения надлежащего physicalmodel воздушного потока в глубоком хорошо с мудрым пунктом выхлопом для приложений контроля в реальном времени. Более точно мы определяем новую модель для главной шахты вентиляции, комнат извлечения и выхлопа, где аэродинамика зависит от атмосферных условий, поверхностного нагревателя и турбины, подземные комнаты эксплуатации и извлечения вентиляторов текут условия. Старт с полного Navier-топит уравнения (сохранение массы, импульс и энергия), 0-D модель, основанная на подходе графа связей, предложена, чтобы смоделировать полную проблему аэрологии шахты. Эта модель включает главную аэродинамику и имеет необходимые возможности в реальном времени к будущим событиям основанных на модели стратегий управления, как иллюстрировано моделированиями. Бумага организована следующим образом. Во-первых, добывающая проблема вентиляции описана, и главные физические свойства обеспечены. 2-я модель, основанная на уравнении Навье-Стокса, представлена в Разделе 3. bondgraph 0-D модель рассматривается в разделе 4 и сопровождается результатами моделирований, которые детализируют динамику потока для определенного прецедента.

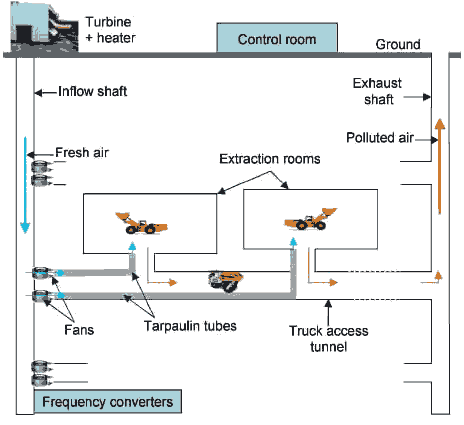
Рисунок 1 – Потоки воздуха в подземной шахте.

1.Описание промышленной вентиляции.

Топология рудничной вентиляции, которую рассматривают в этой работе, представлена в рисунке 1, куда свежий воздух несут от поверхности до комнат извлечения через вертикальную шахту притока и удаляют через выхлопную шахту. С точки зрения контроля эта система вентиляции может быть разделена на две подсистемы: основная система, которая соответствует шахте притока и связанным устройствам автоматизации. Его динамикой управляют, уравнения Навье-Стокса (включая сжимаемость, вязкие потери и термодинамические эффекты), из-за большого массового расхода и длины шахты, которую рассматривают. Отрегулированные входы - нагреватель (используемый в течение зимы в северных странах, чтобы предотвратить замораживание на входе в шахту) и турбинные полномочия. Поклонники, а также атмосферные условия действуют как известные беспорядки на этой системе. Основная система предоставляет поклонникам соответствующее давление потока, которое является тогда отрегулированной продукцией; вторичные системы, которые включают потоки воздуха между (включенными) поклонниками и выходы извлечения помещения. Отметь, что есть одна вторичная система для каждого уровня извлечения. Для этой системы аэродинамика потока может быть значительно упрощена по сравнению с неуверенностью, вызванной сложностью химических процессов. Мы тогда рассматриваем поток воздуха в трубах брезента как невязкий, несжимаемый и адиабатный, и используем полуэмпирическую модель для химических процессов, которая сильно полагается на использование беспроводной сети датчика в комнате извлечения. Вторичное система приводится в действие поклонниками, отрегулированная продукция - газовая концентрация в комнате, и вертикальное давление шахты, а также число грузовиков в комнате - известные беспорядки. Соединение между этими двумя подсистемами - давление в местоположении поклонников, которое является основным параметром, чтобы исследовать относительную эффективность турбины относительно поклонников, чтобы гарантировать, что концентрация газа помещения в пределах границ безопасности. Глобальная проблема моделирования и контроля тогда разделена на две подпроблемы: которые ведут к непрерывной динамике и для которого мы можем получить модель по физическим законам (шахта притока); гибридной динамикой (дискретная часть, являющаяся числом грузовиков в комнате) и очень неуверенная модель, таким образом сильно полагаясь на доступные измерения (вторичные системы). Подробное моделирование и контроль вторичной системы обращены в сопутствующих бумагах[7,8]. Данная работа сосредоточена на аэродинамике, моделирующей в шахтах вентиляции, выделяя поведение большого потока воздуха в глубоком хорошо, и вторичные системы рассматривают как трубы меньшего размера с расширением в местоположениях извлечения помещения.

2. 2-D модель Навье-Стокса.

Мы считаем сжимаемое и вязкое ламинарное течение в вертикальной шахте вентиляции представленным в левой части рис.2 (a), где x - вертикальное направление (с x = 0 на уровне земли и x = L у основания шахты), и y указывает на положение вдоль диаметра. Этот поток характеризуется его плотностью r(x,y,t), скорость V(x,y,t) =u(x,y,t)i+v(x,y,t)j (где i и j - векторы единицы в x и y направлениях), давление p(x,y,t) и температура T(x,y,t). Динамика потока получена из сохранения массы, импульса и энергии, наряду с прекрасным газовым уравнением состояния p=rRT, где R - определенная газовая константа, и гипотеза, что газ - тепловым образом прекрасный e=cvT, где условно является определенной высокой температурой в постоянном объеме.

Выбор консервативной формы (в числовом смысле) уравнения Навье-Стокса у нас есть это[9]: где продукт тензора двух векторов, t - постоянная вектора напряжения, k(x,y,t) теплопроводность,

Рисунок 2 – Вертикальная аэродинамика шахты: 2-D образцовое и усредненное объемом приближение.

H=E+p/r - полное теплосодержание, E - полная энергия на единицу массы.

Используя приписки, чтобы указать на зависимость от частных производных, t вычисляется из того, что sl приписка обозначает условия уровня моря. Теплопроводность получена из k = 1.45 mcp, является определенной высокой температурой в постоянном давлении. Другая возможность состоит в том, чтобы использовать результаты эксперимента, представленные в 11], где бурное распространение и тепловые коэффициенты проводимости в подземных шахтах предложены. Такая модель может быть адаптирована к набору уравнений (1) благодаря надлежащему определению вектора напряжения t.

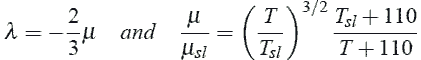
Поскольку мы рассматриваем вязкий поток, определенная забота должна быть проявлена в определении граничных условий (BC). Приток до н.э совпадает с в невязком случае, но стенные условия значительно изменены (без промахов до н.э на скорости и температурном статусе, установленном геотермическим эффектом). Оттоки до н.э также важны, поскольку эксплуатация вентиляторов может дестабилизировать числовую схему. Присутствие пограничных слоев подразумевает особенно усовершенствованную петлю близко к стенам. Произвольные начальные условия (т.е. уровня моря) и классическая схема дискретизации, такие как метод корректора предсказателя, могут использоваться в целях моделирования.

3. 0-D модель Bond-графа.

Безразмерное моделирование есть увеличивающееся использование в дизайне, проверке и настройке законов управления. Два главных преимущества этого подхода - интеграция как можно большего количества физических свойств (избеги отображения данных), и уменьшенное время вычисления (близко к в реальном времени, приблизительно в 10 раз медленнее в худших случаях). Это тогда допускает прогнозирующие модели на неидентифицированных операционных пунктах с удовлетворяющими временами вычисления. Образцовые компоненты, представленные здесь, непосредственно выведены из[12,13] и основанные на 1D уравнения Эйлера (невязкая гипотеза потока).

Эта секция сосредоточена на главной динамике модели и ее применения к добывающему случаю, приводя к представлению графа связей. Мы обращаемся к[12] для более подробного описания. Эта модель основана на уравнении Эйлера, рассматривая уравнение дифференциала времени, которое дискретизировано, используя конечный метод объема. Движущие силы потока в данном объеме контроля непосредственно получены, рассматривая дифференциальный оператор времени как источник внутренней динамики потока и оператора градиента как различие между продукцией и вводят условия потока (см. [12] для получения дополнительной информации). Получающиеся движущие силы упрощены благодаря гипотезам: H1) Только статическое давление рассматривают, подразумевая, что кинетический энергетический термин в уравнении энергосбережения опущен (E =U, внутренняя энергия).

Отметим, что поток теплосодержания непосредственно получен как Qh=QmcpT.

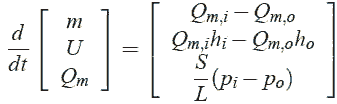
Давление и температура получено из параметров состояния, используя первый закон о Джоулz (U=mcvT) и прекрасные газовые отношения, поскольку Падение давления типично линейно или исключительно, и благодаря уравнению как DP=zQ2m/(2r S2),где z - коэффициент трения.

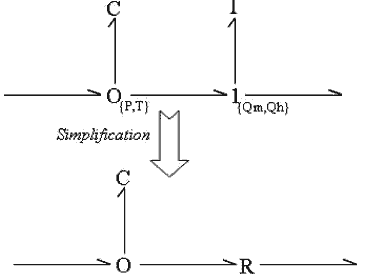
Рисунок 3 – Модель графа связей объема контроля.

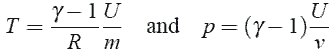
Описание графа связей (см. рис. 3) может теперь быть начато с емкостного C (масса и энергосбережение), индуктивный я (уравнение импульса) и элементы R имеющие сопротивление. Усилия - давление и температура, и потоки - масса и теплосодержание. Элементы имеющие сопротивление введены, чтобы приблизить уравнение импульса с алгебраическими отношениями Венэнта. Это приближение уменьшает числовую нестабильность, введенную индуктивным термином, и допускает больший временной шаг вычисления (рисунок 4).

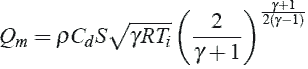
Карта спецификации (синие пункты: экспериментальные значения). Турбина и вентиляторы - компрессоры, которые производят поток в зависимости от градиента давления и скорости вращения. Их особенности зависят от карт спецификации, таких как та, представленная на Рис.4.

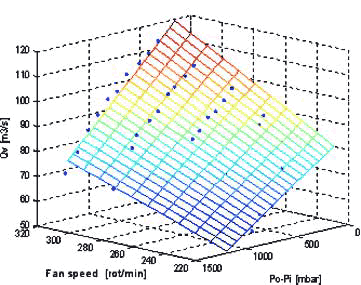
Рисунок 4 – Карта спецификации (синие пунктиры: экспериментальные значения).

Поклонники поток просто пишут как Qh = QmcpT.

Предположим, адиабатное и изотопическое сжатие, температура продукции получена как, где hc - конверсионный фактор эффективности. Модель графа связей наконец построена из предыдущего усилия и отношений потока, используя (4) и (5) для емкостных и элементов имеющих сопротивление, соответственно.

5. Результаты моделирования

Приток и отток шахты вентиляции дискретизированы с 28 объемами контроля. Уровни извлечения (в количестве трех) смоделированы с комнатой и двумя объемами контроля на каждой стороне, как представлено на Рис. 5. Теплообмен введен, в каждом объеме контроля, чтобы принять во внимание геотермический эффект. Это смоделировано с Qp = HcSDT, где Hc зависит от воздушной температуры и потока. Получающийся симулятор, закодированный в Simulink, допускает регулирование турбины и вентиляторов. Потоки, давления и температуры в каждом объеме контроля могут быть измерены. Тематическое исследование, представленное здесь, соответствует следующему сценарию: турбинная скорость вращения увеличена с 260 до 280 об/мин в t=1000 с, 1-й вентилятор уровня не управляется, 2-й уровень идет от 0 до 150 об/мин в t = 2000 с и 3-й уровень управляются в 200 об/мин во время целого моделирования.

Рисунок 5 – Модель HynX 0D рудничной вентиляции.

Загрязнение СО введено в t =500 с в течение 80 с в 3-й выработке уровня. Развитие времени поток, давление, температура и загрязнение измерены на уровнях извлечения и поверхности. Результаты моделирования, представленные на Рис. 6, иллюстрируют развитие времени физических и химических свойств потока воздуха для сценария, описанного выше на различных глубинах. Падение давления в шахте притока (Рис.6 (a)), который шоу, которое энергетические потери связались с транспортом потока в глубоком хорошо, увеличение, связало с турбинным дополнительным приведением в действие и решительным падением давления, которое происходит, когда поклонник 2 включен. Темп вентиляции помещения (Рис.6 (b)) основной момент физическое соединение между комнатами и важностью глобальной стратегии управления для основной системы. Температурное развитие (Рис.6 (c), где мы выбрали особенно холодное начальное условие подчеркнуть динамику) стимулирует геотермический эффект и сильно затрагивает сжатие поклонников. Мы также в состоянии принять во внимание загрязнитель NOx and/or CO и отследить развитие концентрации вдоль выхлопной шахты (Рис.6 (d)): эффект с временной задержкой, связанный с транспортным явлением, особенно выделен. Время вычисления очень удовлетворяет, поскольку моделирование в 34 раза быстрее, чем в реальном времени в Intel Centrinor 1.83 GHz PC. Предложенная 0-D модель эффективно предусматривает быструю и представительную глобальную модель проблему рудничной вентиляции. Действительно, хорошая количественная оценка главной динамики и связанных задержек получена несмотря на относительно низкое число государств. Точность может быть увеличена, увеличивая число объемов контроля и связанное число параметров состояния, но у этого есть прямое следствие на времени моделирования. Предложенное моделирование основано на 142 параметрах состояния (28 клеток за шахту, 5 клеток за уровень извлечения и 2 государства за клетку) и в 34 раза быстрее, чем в реальном времени, который особенно подходит для дизайна законов управления.

Выводы

В этой работе, мы решили проблему обеспечения соответствующей модели для горной промышленности контроля за вентиляцией как проблему моделирования, сосредоточенную на аэродинамике потока. Рассмотрели два различных класса моделей: классическое 2-D уравнение Навье-Стокса и 0-D модель графа связей. Несколько проблем, таких как турбулентность, нелинейность и соединения, были кратко обсуждены. Главная цель моделей тезисов состоит в том, чтобы мотивировать будущие работы над основанным на модели контролем в реальном времени (результаты моделирования 0-D модел иллюстрируют его полноценность для таких заявлений), продвинутые основанные на PDE стратегии управления (1-D модель) или разработка сложных симуляторов для анализа потоков (2-D модель).

При моделировании пользователь может выбирать метод решения дифференциальных уравнений, а также способ изменения модельного времени (с фиксированным или переменным шагом). В ходе моделирования имеется возможность следить за процессами, происходящими в системе. Для этого используются специальные устройства наблюдения, входящие в состав библиотеки Simulink. Результаты моделирования могут быть представлены в виде графиков или таблиц.

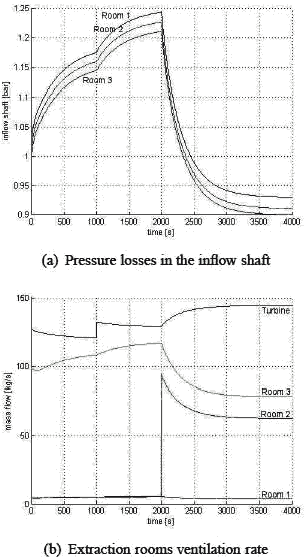
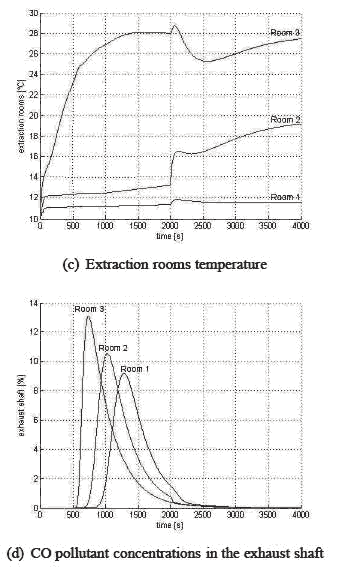
Рисунок 6 – Результаты моделирования для 3-уровневой шахты.(а)Падение давления в шахте притока; (b)Темп вентиляции добычной выработки; (c)Температура в добычной выработке; (d)Концентрации загрязнителя CO в вентиляционной шахте

Список использованной литературы

1. S. Tolmachev and E. Fainshtein, “Analysis of multibranch junctions in ventilation networks, regarded as systems with distributed parameters,” Journal of Mining Science, vol. 4(2), pp. 128–133, 1968.
2. F. Klebanov and G. Martynyuk, “A method for experimental determination of the coefficient of longitudinal turbulent diffusion in ventilating currents of mine workings,” Journal ofMining Science, vol. 9(4), pp. 413–416, 1973.
3. G. Kalabin, A. Baklanov, and P. Amosov, “Calculating the aerogas dynamics of chamber-like mine workings on the basis of mathematical modeling,” Journal of Mining Science, vol. 26(01), pp. 61–73, 1990.
4. N. Petrov, M. Shishkin, V. Dnitriev, and V. Shadrin, “Modeling mine aerology problems,” Journal of Mining Science, vol. 28(2), pp. 185–191, 1992.
5. N. Petrov, “Methods of solving problems and designing equipment for mine ventilation,” Journal of Mining Science, vol. 30(2), pp. 195–204, 1994.
6. E. Widzyk-Capehart and B. Watson, “Agnew gold mine expansion mine ventilation evaluation using VentSim,” in Proc. of the 7th International Mine Ventilation Congress, 2001.
7. S. Olaru, G. Sandou, E. Witrant, and S. Niculescu, “Receding horizon climate control in metal mine extraction rooms,” in Submitted to IEEE CASE’08, 2008.
8. M. Di Benedetto, A. D’Innocenzo, E. Serra, and E. Witrant, “Automatic verification of wireless control in a mining ventilation system,” in Submitted to IEEE CASE’08, 2008.
9. C. Hirsch, Numerical Computation of Internal & External Flows: the Fundamentals of Computational Fluid Dynamics, 2nd ed. Butterworth-Heinemann (Elsevier), 2007.
10. J. Brown, A. Vardy, and A. Tijsseling, “Response of wall heat transfer to flows along a cylindrical cavity and to seepage flows in the surrounding medium,” Eindhoven: Technische Universiteit Eindhoven, Tech. Rep., 2005. [Online]. Available: ftp://ftp.win.tue.nl/ pub/rana/rana05-35.pdf
11. G. Averin and A. Yakovenko, “Determination of the turbulent diffusion and heat-conduction coefficients in mine workings,” Journal of Mining Science, vol. 26(5), pp. 465–467, 1990.
12. V. Talon, “Mod?elisation 0-1 d des moteurs `a allumage command?e,” Ph.D. dissertation, Universit?e d’Orl?eans, 2004.
13. V. Talon and S. Cstric, “Engine control model based design with achille library,” E-COM: Re