Моделювання системи електромеханічних властивостей асинхронного двигуна з короткозамкнутим ротором при частотному регулюваннішвидкості на насосних станціях
Автор: В. В. Гузенко, інж., М. Л. Лисиченко, докт. техн. наук
Источник: Светотехника и электроэнергетика №2, 2011р. – Харків, Харківський національний технічний
університет сільського господарства ім.Петра Василенка, 2011. с.50 – 54.
Постановка задачі. В сучасному сільському господарстві основними споживачами є електродвигуни (понад 60 %) [1]. За рахунок цього до них висувають все більш жорсткі вимоги, щодо ефективності роботи: рівень втрат енергії, відповідність навантаження, ін. При цьому, в останній час найбільш пріоритетне значення, на ряду з оптимальним конструюванням асинхронних двигунів (АД), набувають задачі оптимального моделювання електроприводів змінного струму та визначення ефективних режимів роботи [2].
Існує багато способів регулювання швидкості, наприклад: зміною напруги живлення, введення додаткових опорів в коло статора або ротора, зміною магнітного потоку, імпульсно-фазний спосіб та регулювання за допомогою перетворювача частоти. Аналіз способів регулювання швидкості обертання приводів показує, що перспективним є частотне регулювання частотою обертання електроприводів завдяки плавності регулювання швидкості і значного зниження енергоспоживання на основі використання асинхронно-вентильний каскад [3].
Саме використання комп’ютерного математичного моделювання з розробкою моделей різних пристроїв дозволяє провести розрахунки процесів з високою точністю, а також дослідити електромеханічні властивості перед запровадженням в дію такого способу регулювання.
Мета дослідження. Дослідження електромеханічних властивостей АД при частотному регулюванні кутової швидкості, встановлення математичних залежностей, розробка їх на основі методик.
Аналіз останніх досліджень. Система АВК була вперше запропонована в 1937 році Ф.І Бутаєвим, Г.Б Еттингером. Подальший розвиток роботи по вентильним каскадам отримали в трудах М.П Костенко, Ф.І Буттєва [4].
Можливість керування частотою обертання АД була доведена зразу після винаходу електродвигуна. Як правило, керування електроприводом змінного струму здійснюється за рахунок зміни вихідних параметрів силового перетворювача (fм, Uм). Реалізувати цю можливість вдалося лише з появою силових полупровідникових пристроїв (тиристорів) [4].
В залежності від характеру навантаження перетворювач частоти забезпечує різні режими керування електродвигуном, реалізовуючи ту чи іншу залежність між швидкістю обертання електродвигуном та вихідною напругою. Тому необхідно використовувати імітаційне моделювання з використанням ЕВМ. Такий підхід дозволить спрогнозувати результати з високою точністю.
Частотний спосіб управління заснований на законі М.П. Костенко, який встановив, що відносне діюче значення напруги необхідно змінювати пропорційно добутку частоти на корінь квадратний з відносного моменту двигуна. Надалі А.А. Булгаковим були встановлені закономірності різних співвідношень між частотою і діючим значенням напруги: напруга змінювалася пропорційно частоті; Uм ? fм; напруга змінювалася так, щоб забезпечити сталість повного або робочого потоку при зміні частоти; керування частотою при номінальній напрузі ін.;
Великий внесок у розвиток теорії частотного управління внесли А.С. Сандлер, Р.С. Сарбатов, І.І. Епштейн, які розглянули як статичні, так і динамічні режими роботи АД при живленні від перетворювачів частоти (ПЧ).[6]
Основні матеріали досліджень. Використання регульованого електропривода дозволяє скоротити енергоспоживання: помп – на 25-30 %, компресорів – на 40 %, вентиляторів – на 30 %, центрифуг – на 50 %. Зважаючи на те, що ці типи механізмів складають більше 50 % використовуваних у сільському господарстві приводів, даний напрямок є пріоритетним для економії електроенергії.
Найбільш перспективними напрямами впровадження регульованих електроприводів у сільськогосподарському виробництві є системи водопостачання, теплопостачання, каналізації, вентиляції будівель. Оптимальний мікроклімат – комплекс чинників зовнішнього середовища, які сприяють найкращому прояву фізіологічних функцій організму тварин і птиці, отриманню максимальної продукції при найменших витратах кормів [7].
Система водопостачання – це досить складний комплекс взаємозалежних по параметрах і режимам роботи спеціальних споруд, що забезпечує забір води з джерел водопостачання, її обробку, акумулювання і збереження, подачу до місця споживання, а також розподіл між її споживачами. У кожній точці мережі напір води повинен підтримуватися на заданому рівні, що забезпечує якісне обслуговування споживачів води. Напір у мережі залежить від роботи водо живильників, а також від споживання води, що носить випадковий характер.
У роботі проведено моделювання системи автоматичного регулювання швидкості АД в программі MATLAB Simulink. Дослідження базувалися на теорії диференціальних рівнянь, на комп'ютерних методах моделювання. Створена модель містить у своєму складі готовий блок електроприводу з джерелом живлення, частотним перетворювачем і асинхронним двигуном, та технологічну частину – модель насосного агрегату та модель водоводів (рис. 1)
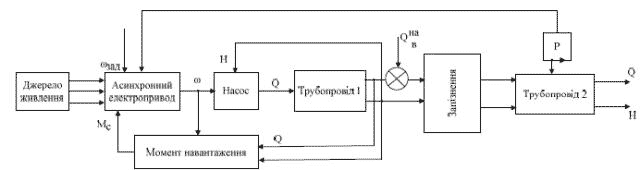
Рисунок 1 – Модель насосної станції системи водопостачання
Дослідження проводились на насосних станціях з приводом потужністю 11,5 кВт та 22,5 кВт. Для регулювання частоти обертання електроприводу насосних установок в залежності від тиску води в розбірному трубопроводі застосовували перетворювач частоти типу ПЧРТ-03-22. Дослідження проводилось на реальній установці на базі водопідйому “Карлівка” Полтавської області. Частотний спосіб до того ж відрізняється і ще одним досить важливою властивістю: при регулюванні швидкості АД не відбувається збільшення його ковзання, як це має місце, наприклад, при реостатному регулюванні. Тому при цьому способі регулювання втрати ковзання, виявляються невеликими, у зв'язку, з чим частотний спосіб найбільш економічний.
При вирішенні системи диференціальних рівнянь, що описують роботу системи АД-ПЧ, використовували метод Рунге-Кутта в модифікації Гіра.
Склавши модель системи ПЧ-АД в пакеті MatLab 6.5, отримали

Рисунок 2 – Модель системи ПЧ-АД для программного пакета MatLab 6.5
Моделюємо пуск двигуна без навантаження при трьох різних частотах живлячої напруги f1 = 50 Гц, f2 = 37,5 Гц, f3 = 25 Гц, використовуючи закон частотного регулювання U/(f)1/2 = const. Значить при f=50 Гц; Uл=380 В; при f=37,5 Гц Uл=329 В; при f=25 Гц Uл=269 В.
При частоті живильної мережі f = 50 Гц і лінійному напрузі Uл = 380 В отримуємо наступні графіки перехідних процесів ω = f(t) (рад/с) и Mв = f(t) (Н·м).
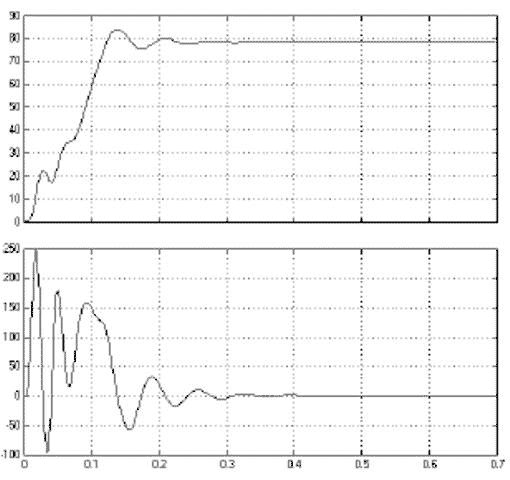
Рисунок 3 – Графики ω=f(t) и Mв=f(t). при f=50 Гц |
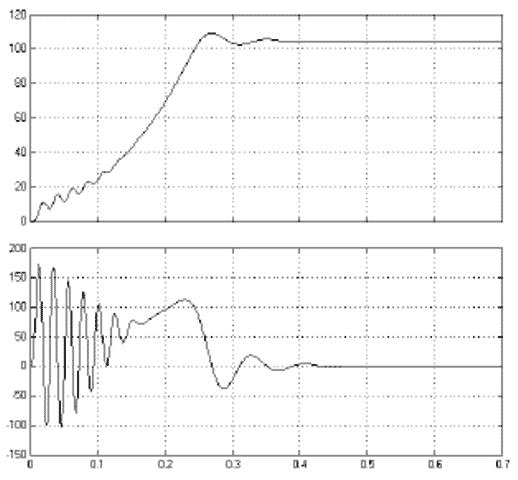
Рисунок 4 – Графики ω=f(t) и Mв=f(t). при f=37,5 Гц |
Після закінчення перехідного процесу одержуємо такі усталені значення: ω =104,7 рад/с, I1=7,266 А, Mв=0,517 Н·м
При частоті живильної мережі f = 37,5 Гц і лінійному напрузі Uл = 329 В отримуємо наступні графіки перехідних процесів ω=f(t) (рад/с) и Mв=f(t) (Н·м).

Рисунок 5 – Графики ω=f(t) и Mв=f(t). при f=25 Гц |
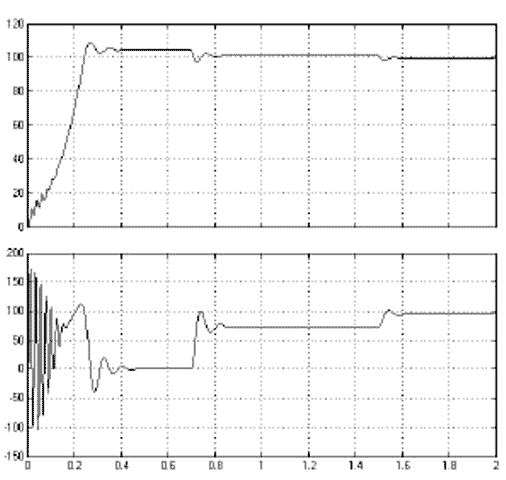
Рисунок 6 – Наброс навантаження Мс.доп.=0,3Мн |
Після закінчення перехідного процесу одержуємо такі усталені значення: ω =78,53 рад/с, I1=7,608 А, Mв=0,3883 Н·м
При частоті живильної мережі f = 25 Гц і лінійному напрузі Uл = 269 В отримуємо наступні графіки перехідних процесів ω=f(t) (рад/с) и Mв=f(t)(Н·м). Після закінчення перехідного процесу одержуємо такі усталені значення: ω =52,36 рад/с, I1=10,29 А, Mв=0,036 Н·м
При частоті живильної мережі f = 50 Гц і лінійному напрузі Uл = 380 В змоделюємо перехід системи з одного сталого стану Мв=Мн=73 Н?м, ω=ωн=101.7 рад/с, I1 = I1н = 15,65 А) в інше після набросу навантаження на вал двигуна (Мс.доп.= 0,3Мн = 22 Н·м).
Для більш детального вивчення перехідного процесу на рис. 7. наведена збільшена частина графіків ω=f(t) (рад/с) и Mв=f(t) (Н·м), охоплює тільки момент уповільнення двигуна після набросу додаткового навантаження.

Рисунок 7 – Наброс навантаження Мс.доп.=0,3Мн (фрагмент)
Після закінчення перехідного процесу одержуємо такі усталені значення: ω =99,7 рад/с; I1=20,06 А; Mв=95,5 Н·м
Регулювання в цій системі, може здійснюватися плавно, в широкому діапазоні, в обидві сторони від природньої характеристики, тобто АД, може мати швидкість як більше, так і менше номінальної. При цьому регулювальні характеристики мають високу жорсткість, а АД зберігає більшу перевантажувальну здатність.
Висновки. Дослідження свідчить про те, що регулювання швидкості асинхронного двигуна, з використанням частотного перетворювача, дозволяє не тільки відредагувати технологічний процес, а і зменшити втрати та зекономити електроенергію від 20 % до 40 %, а також плавно регулювати швидкість обертання електродвигуна від нуля до номінального значення при збереженні максимального моменту на валу, що дало можливість збільшити термін служби і підвищити надійність електроприводів та обладнання і підвищити якість надання послуг у водопостачанні за рахунок стабільного тиску в мережі.
По результатам дослідження слід відзначити що доцільно використовувати перетворювачі частоти не в якості елементів системи керування конкретного агрегату, а як комплекс системних рішень з підключенням широкого набору засобів автоматизації технологічного процесу. Створена комп’ютерна модель дозволяє моделювати роботу системи керування електроприводу насосної станції системи водопостачання. Плавне регулювання швидкості в широких межах з зберіганням достатньої жорсткості характеристик можливо тільки при частотному керуванні, що дало суттєве зниження аварійності мережі і насосної установки.
Література:
- Булгаков А.А. Частотное управление асинхронными двигателями. – М.: Энергоиздат, 1982
- Копылов И.П. Математическое моделирование электрических машин: Учеб. для вузов. – 3-е изд., переработ. и доп. – М.: Высш.шк., 2001. – 327 с.
- Овчинников И.Е. Вентильные электрические двигатели и привод на их основе. – СПб.: КОРОНА-Век, 2006.
- Масандилов Л.Б Регулирование частоты вращения асинхронных двигателей. М.: –Энергия, 1978 . – 96 с.
- Сипайлов Г.С.,Лоос А.В. Математическое моделирование электрических машин. –М.: Высшая школа,1980. – 176 c.
- Корчемний М.О. Енергозбереження в АПК. Підручник для студентів вищих навчальних закладів.– Тернопіль: 2001, 984с.
- Ковач К., Рац И. Переходные процессы в машинах переменного тока. – М. – Л., Госэнергоиздат,1963. –744 c.
- Высоцкий В.Е., Зубков Ю.В., Тулупов П.В. Математическое моделирование и оптимальное проектирование вентильных электрических машин. – М.: Энергоатомиздат, 2007.
- Герман-Галкин Г. Компьютерное моделирование полупроводниковых систем в Mathlab 6.0. – М.: Коронапринт, 2001. – 320 с.
- Эпштейн И.И. Автоматизированный электропривод переменного тока. – М.: Энергоатомиздат,1982. – 192 c.
- Петров Л.П., Ладензон В.А., Подзолов Р.Г., Яковлев А.В. Моделирование асинхронных электроприводов с тиристорным управлением. – М.: Энергия, 1977. – 200 c.
- Беспалов В. Я. Перспективы создания отечественных электродвигателей нового поколения для частотно-регулируемого электропривода, – М.: МЭИ (ТУ), 2005.
- Герман-Галкин Г., Кардонов Г.А. Электрические машины: Лабораторные работы на ПК. – СПб.: КОРОНА принт, 2007. –256 с.