Моделирование и управление температурой в теплообменных процессах

Введение.

Для обмена тепла между двумя жидкостями с различными температурами и с высокой эффективностью широко используются теплообменники в таких отраслях, как переработка газа, нефтехимической промышленности и так далее. В этой области корпус и трубка теплообменника используются для нагрева или охлаждения технологических жидкостей. Корпус состоит из параллельных труб, заключенных в оболочки. В основном эти теплообменники используются для высокого давления (с давлением, превышающим 30 бар и температурой выше 260 ° С). Но главной проблемой теплообменного процесса является отклонение температуры от заданной уставки. [2] Моделирование процесса в теплообменнике для оценки температуры горячей и холодной жидкости на выходе, в зависимости от скорости потока и температуры на входе, осуществляется с помощью оптимизированной архитектуры искусственной нейронной сети.

Рисунок 1 – U-образный теплообменник

Алгоритм, который обучает нейронную сеть, от 10 до 100 раз быстрее, чем обычный алгоритм обратного распространения. Название этого алгоритма – алгоритм Левенберга-Марквардта. В то время как обратное распространение является алгоритмом крутого спуска, алгоритм Левенберга-Марквардта является вариацией метода Ньютона. Этот алгоритм обеспечивает хорошую взаимосвязь между скоростью Гаусса-Ньютона и гарантированной сходимостью наискорейшего спуска. [3] В этом обучающем алгоритме наблюдение за обучением используется там, где целевые значения для выхода подаются в сеть надлежащим образом для обновления веса сети. Различные параметры, а именно: входные и выходные температуры оболочки и боковые трубки жидкости, и их расход, необходимо принять во внимание при разработке модели. Искусственные нейронные сети (ИНС) эффективны при моделировании нелинейных связей нескольких переменных, а также упоминается в моделях черного ящика. Во-первых, классический ПИД-регулятор выполнен в контуре обратной связи так, чтобы обеспечить управление объектами. Для дальнейшей оптимизации характеристик управления упреждающий контроллер используется в сочетании с ПИД-регулятором. В данной работе реализуется и моделируется автоматическая настройка ПИД-регуляторов, а также оценивается, в сравнении со всеми изученными, управление характеристиками.

Моделирование теплообменного процесса.

Модель искусственной нейронной сети разработана с использованием оптимизированной архитектуры для моделирования теплообменника с целью оценки температуры горячей и холодной жидкости на выходе в зависимости от скорости потока и температуры на входе. Данные, необходимые для этой сети, былы сформированы в случае с использованием воды с 20 % содержанием глицерина. После различных режимов используют эксперементальную генерацию данных.

Таблица 1 – Режимы создания данных

В этой модели, в которой сравнивается реальная и прогнозируемая температуры, текущие данные теплообменника применяются для обучения модели нейронной сети инструментом "n-f tool" в Matlab. Система автоматически принимает 60 % данных для обучения, 20 % для проверки и 20 % для тестирования, так что одни и те же данные не будут использоваться только для тестирования. Это требует много усилий для приближения или получения ожидаемого результата обучения.

После того как система прошла обучение, ее отправляют к остальным образцам данных для тестирования. Для определения параметров модели первого порядка дважды измеряются: t1 – время, когда выходное значение производства достигает 28,3 % от последнего измерения в стационарной точке Yf – Yi, и t2 – время, в которое выходное значение составляет 63,2 % от Yf – Yi. На рисунке 1, t1 = 27,792 и t2 = 36,168. Применив метод идентификации к модели первого порядка, представленной на рисунке 2, получим:

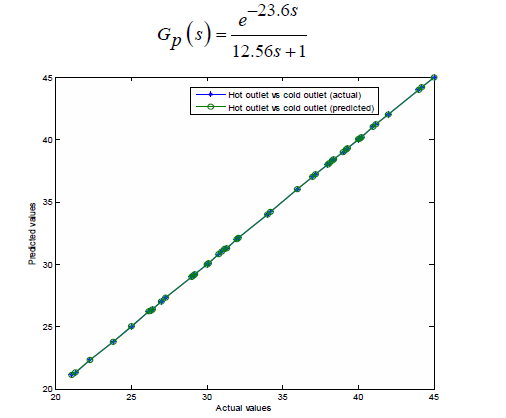
Рисунок 2 – Фактические и прогнозируемые значения горячей и холодной жидкости

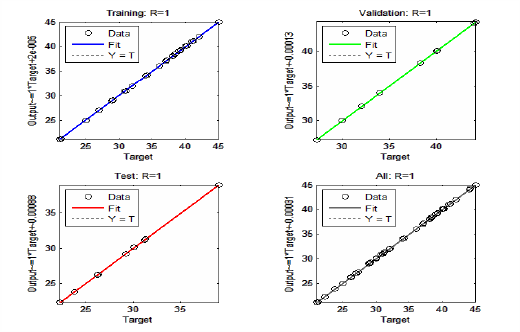
Рисунок 3 – Графики регрессий фактических и прогнозируемых результатов для упреждающей модели нейронной сети для обучения, проверки, тестирования и всего набора данных

На рисунке 3 пунктирная линия является идеально соответствующей линией, где выходные и целевые значения равны друг другу. Круги – точки значений, а цветные линии наилучше отображают соответствие между выходными и целевыми значениями. Здесь важно отметить, что круги располагаются вдоль пунктирной линии, поэтому наши выходные значения находятся недалеко от целевых. Из графика видно, что это может быть реализовано лучше, чем скрытый блок с 99 % точностью только с одним нейроном, который используется как пробный в этой моделе.

Рисунок 4 – Показано обучение, проверка и тестирование среднеквадратичной ошибки для алгоритма Левенберга-Марквардта с одним нейроном

На рисунке 4 представлены обучение, проверка и тестирование среднеквадратичной ошибки для алгоритма Левенберга-Марквардта с одним скрытым нейроном. Обучение останавливается, когда среднеквадратичная ошибка не меняется.

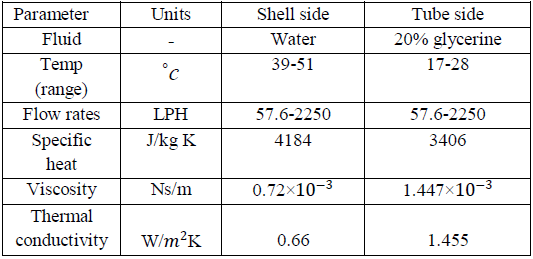
Таблица 2 – Оценка эффективности подготовки, проверки и тестирования

Таблица 3 – Оценка эффективности подготовки, проверки и тестирования

Постановка задачи.

В этом разделе мы разработали блок-схему из контуров управления и промоделировали систему теплообменника, привод, клапан, датчик с использованием экспериментальных доступных данных. Модели передаточных функций отдельных систем, в свою очередь, объединяются для получения передаточной функции всей системы. Из приведенных выше экспериментальных данных получена модель передаточной функции системы.

Передаточная функция процесса.

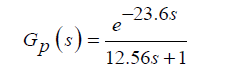
Коэффициент усиления вентиля 0,133;

Передаточная функция вентиля 0,133 / (3s + 1);

Коэффициент усиления преобразователя 0,75;

Передаточная функция термопары 0,16 / (10s + 1);

А. ПИД-регулятор.

Характеристическое уравнение (1 + G (S) *  H (S) = 0), в этом случае, получено, как

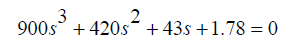
ПИД-регулятор традиционно подходит для систем второго и более низкого порядка. Он также может быть использован для более высокого порядка с преобладающим поведением второго порядка. ПИД-регулятор настраивается в соответствии с таблицей, которая основана на тестировании ответного процесса. Согласно методу Зиглера-Никольса получен критерий настройки реакции АЧХ.

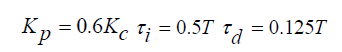
Для ПИД-регулятора в теплообменнике значения параметров настройки имеют вид: P = 0,4636 I = 0,045 D = 1,18

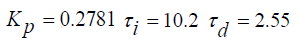
Рисунок 4 ясно показывает, что задержка будет влиять на шаг реакции процесса до момента времени 23,6 с. и после этого следует ступень отклика.

Рисунок 4– Реакция ПИД-;регулятора

Теперь различные значения Kp, то есть 0,2781 и 0,4636, используются и изменяются в зависимости от реакции на единичный скачок, как показано на рисунке 4.

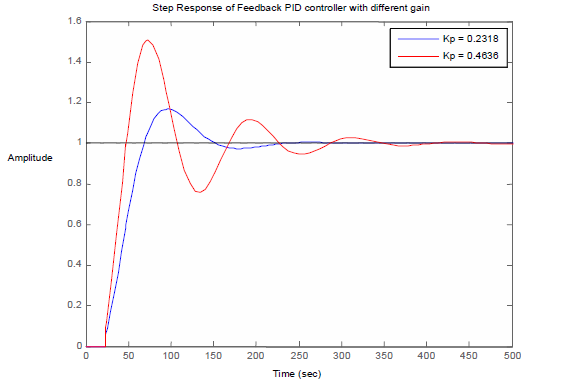
Рисунок 5– ПИД-;регулятор с обратной связью при различных коэффициентах усиления

Б. Регулятор с обратной связью и упреждающий регулятор.

Упреждающий регулятор подсчитывает приблизительно ошибку и меняет воздействующую переменную перед нарушением, которое может повлиять на выходное значение. Для дальнейшей минимизации ошибки, упреждающий регулятор вводится в прямой канал модели вместе с регулятором обратной связи. Комбинированный эффект регулятора с обратной и прямой связью приводит к снижению значения ошибки. В упреждающем регуляторе мы постарались регулировать ошибку входного потока жидкости. Gp (s) передаточная функция системы, где Gd (s) передаточная функция возмущающего потока.

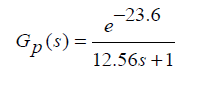
Рисунок 6 – Реакция упреждающего регулятора с положительной обратной связью

Из рисунка 6 видно, что упрежающий регулятор с положительной обратной связью обеспечивает лучшее быстродействие по сравнению с ПИД-регулятором. Также упреждающий регулятор с положительной обратной связью позволяет уменьшить ошибку раньше по сравнению с ПИД–регулятором. Значения ошибки и время установления меньше по сравнению со значениями ПИД-регулятора.

В. Сравнение различных параметров в регуляторах.

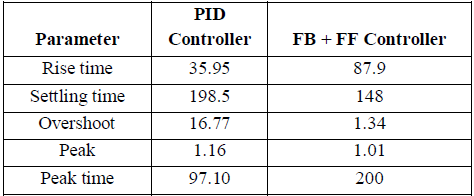
Таблица 4– Сравнение различных параметров в регуляторах

Заключение.

Для эффективного регулирования температуры существует три вида регуляторов, и моделирование теплообменника осуществляется с помощью искусственной нейронной сети. Можно сделать вывод, что модели теплообменника с исскуственными нейронными сетями с использованием алгоритма Левенберга-Марквардта для воды с 20 % содержанием глицерина имеют высокий класс точности (99 % – 99,5 %) и их целесообразней использовать. Классический ПИД-регулятор предназначен для достижения управления, но в связи с неудовлетворительной работой ПИД-регулятора с прямой связью, упрежденный регулятор утвержден и помещен в прямой канал системы. Также отмечено, что упреждающий регулятор с положительной обратной связью имеет более высокое быстродействие, чем обычный ПИД-регулятор.

Список использованной литературы

 1. S. L. Pandharipande, M. A/ Siddiqui, A. Dubay& S. A. Mandavgane, Application of Optimum ANN Architecture for Heat Exchanger Modeling, Indian Journal of Chemical Technology, Volume 13, November 2006, pp. 634 – 639.
  2.Subhransu Padhee and Yaduvir Singh, A Comparative Analysis of Various Control Strategies Implemented on Heat Exchanger System: A case study, Proceeding of the World Congress on Engineering ,Volume II, WCE 2010, pp. 873 – 877
  3. S. A. Mandavgane & S. L. Pandharipande, Application of ANN for Modelling of Heat Exchanger with Concentration as Variable, Indian Journal of Chemical Technology, Volume 13, March 2006, pp 173 – 176.
  4 .Yuvraj Bhushan Khare and Yaduvir Singh, PID Control of Heat Exchanger System, International Journal of Computer Applications, Volume 8, October 2010, 22 – 27.
  5.Hagan and Menhaj, Training feed forward networks with the Marquardt algorithm, IEEE Trans. on Neural Networks, Volume 6, 1994, pp. 989 – 993.
  6. S. L. Pandharipande, M. A. Siddiqui, A. Dubay & S. A. Mandavgane, Optimising ANN Architecture for Shell and Tube Heat Exchanger Modelling, Indian Journal of Chemical Technology, Volume 11, November 2004, 804 – 810.