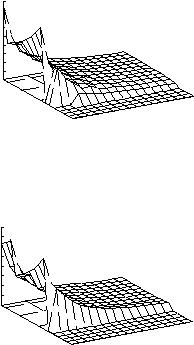
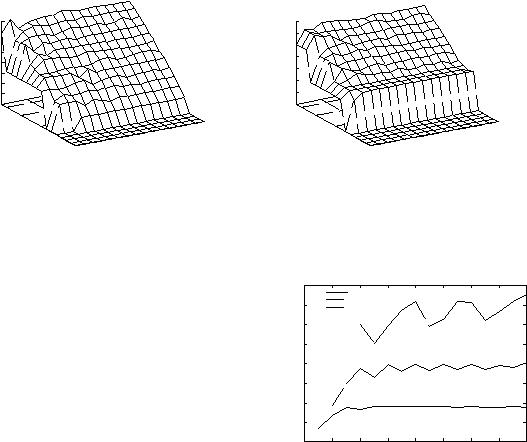
impact of off-chip memory access latency. Many mod- ern NP architectures use multithreading and we intend to expand our model to take this into consideration.
We believe that the performance model that we pro- vide in this work is a valuable tool for fast, quantitative design space exploration of network processor system topologies. This can help in determining how future NP architectures can be designed to provide the necessary scalability to support increasing link rates and increasing application complexity.
Acknowledgements
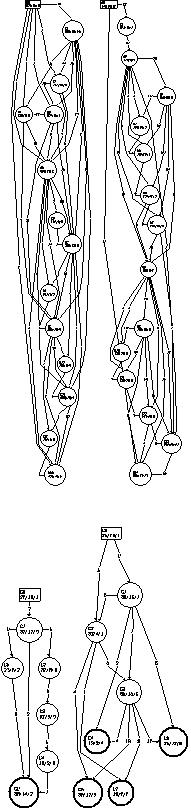
The authors would like to thank Ramaswamy Ra- maswamy for providing the run-time instruction traces that were used for the ADAG generation.
References
[1]F. Baker. Requirements for IP version 4 routers. RFC 1812, Net- work Working Group, June 1995.
[2]D. P. Bhandarkar. Analysis of memory interference in multi- processors. IEEE Trans. on Computers, c-24(9):897–908, Sept. 1975.
[3]D. Burger and T. Austin. The SimpleScalar tool set version 2.0.
Computer Architecture News, 25(3):13–25, June 1997.
[4]P. Crowley and J.-L. Baer. A modelling framework for network processor systems. In proc. of Network Processor Workshop in conjunction with Eighth International Symposium on High Per- formance Computer Architecture (HPCA-8), pages 86–96, Cam- bridge, MA, Feb. 2002.
[5]P. Crowley, M. E. Fiuczynski, J.-L. Baer, and B. N. Bershad. Characterizing processor architectures for programmable net- work interfaces. In Proc. of 2000 International Conference on Supercomputing, pages 54–65, Santa Fe, NM, May 2000.
[6]J. Daemen and V. Rijmen. The block cipher Rijndael. In Lec- ture Notes in Computer Science, volume 1820, pages 288–296. Springer-Verlag, 2000.
[7] EZchip Technologies Ltd., |
Yokneam, |
Israel. |
NP- |
1 |
10-Gigabit |
7-Layer |
Network |
Processor, |
2002. |
http://www.ezchip.com/html/pr np-1.html. |
|
|
[8]M. A. Franklin and T. Wolf. A network processor performance and design model with benchmark parameterization. In P. Crow- ley, M. A. Franklin, H. Hadimioglu, and P. Z. Onufryk, edi- tors, Network Processor Design: Issues and Practices, Volume 1, chapter 6, pages 117–138. Morgan Kaufmann Publishers, Oct. 2002.
[9]M. A. Franklin and T. Wolf. Power considerations in network processor design. In M. A. Franklin, P. Crowley, H. Hadimioglu, and P. Z. Onufryk, editors, Network Processor Design: Issues and Practices, Volume 2, chapter 3. Morgan Kaufmann Publishers, Nov. 2003.
[10]P. A. Grasso et al. Memory interference in multimicroproces- sor systems with a time-shared bus. Proceedings of the IEEE, 131(10), Mar. 1984.
[11]M. Gries, C. Kulkarni, C. Sauer, and K. Keutzer. Exploring trade- offs in performance and programmability of processing element topologies for network processors. In Proc. of Network Processor Workshop in conjunction with Ninth International Symposium on High Performance Computer Architecture (HPCA-9), Anaheim, CA, Feb. 2003.
[12]C. H. Hoogendoorn. A general model for memory interference in multiprocessors. IEEE Trans. on Computers, c-26(10):998–1005, Oct. 1977.
[13]Intel Corp. Intel IXP1200 Network Processor, 2000. http://www.intel.com/design/network/products/npfami- ly/ixp1200.htm.
[14]Intel Corp. Intel Second Generation Network Processor, 2002. http://www.intel.com/design/network/products/npfami- ly/ixp2400.htm.
[15]R. M. Karp. An introduction to randomized algorithms. Discrete Applied Mathematics, 34(1-3):165–201, Nov. 1991.
[16]Y.-K. Kwok and I. Ahmad. FASTEST: A practical low- complexity algorithm for compile-time assignment of parallel programs to multiprocessors. IEEE Trans. Parallel Distributed Systems, 10(2):147–159, Feb. 1999.
[17]Y.-K. Kwok and I. Ahmad. Static scheduling algorithms for allo- cating directed task graphs to multiprocessors. ACM Computing Surveys, 31(4):406–471, Dec. 1999.
[18]V. Lakamraju, I. Korean, and C. M. Krishna. Filtering ran- dom networks to synthesize interconnection networks with mul- tiple objectives. IEEE Trans. Parallel Distributed Systems, 13(11):1139–1149, Nov. 2002.
[19]Lucent Technologies Inc. PayloadPlusTM Fast Pattern Processor, Apr. 2000. http://www.agere.com/support/non- nda/docs/FPPProductBrief.pdf.
[20]B. A. Malloy, E. L. Lloyd, and M. L. Souffa. Scheduling DAG’s for asynchronous multiprocessor execution. IEEE Transactions on Parallel and Distributed Systems, 5(5):498–508, May 1994.
[21]G. Memik, W. H. Mangione-Smith, and W. Hu. NetBench: A benchmarking suite for network processors. In Proc. of Interna- tional Conference on Computer-Aided Design, pages 39–42, San Jose, CA, Nov. 2001.
[22]R. Motwani and P. Raghavan. Randomized Algorithms. Cam- bridge University Press, New York, NY, 1995.
[23]National Laboratory for Applied Network Research - Passive Measurement and Analysis. Passive Measurement and Analysis, 2003. http://pma.nlanr.net/PMA/.
[24]S. Nilsson and G. Karlsson. IP-address lookup using LC-tries.
IEEE Journal on Selected Areas in Communications, 17(6):1083– 1092, June 1999.
[25]R. Ramaswamy, N. Weng, and T. Wolf. Application analysis and resource mapping for heterogeneous network processor architec- tures. In Proc. of Network Processor Workshop in conjunction with Ninth International Symposium on High Performance Com- puter Architecture (HPCA-10), pages 103–119, Madrid, Spain, Feb. 2004.
[26]R. Ramaswamy and T. Wolf. PacketBench: A tool for workload characterization of network processing. In Proc. of IEEE 6th An- nual Workshop on Workload Characterization (WWC-6), pages 42–50, Austin, TX, Oct. 2003.
[27]G. L. Reijns and A. J. C. van Gemund. Analysis of a shared- memory multiprocessor via a novel queuing model. Journal of Systems Architecture, 45(14):1189–1193, 1999.
[28]TCPDUMP Repository. http://www.tcpdump.org, 2003.
[29]L. Thiele, S. Chakraborty, M. Gries, and S. Kunzli¨. Design space exploration of network processor architectures. In Proc. of Net- work Processor Workshop in conjunction with Eighth Interna- tional Symposium on High Performance Computer Architecture (HPCA-8), pages 30–41, Cambridge, MA, Feb. 2002.
[30]A. J. C. van Gemund. Performances prediction of parallel pro- cessing systems: The pamela methodology. In Proc. 7th ACM International Conference on Supercomputing, pages 318–327, Tokyo, Japan, July 1993.
[31]Y.-C. Wei and C.-K. Cheng. Ratio cut partitioning for hierarchi- cal designs. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 10(7):911–921, July 1991.
[32]T. Wolf and M. A. Franklin. CommBench - a telecommunica- tions benchmark for network processors. In Proc. of IEEE In- ternational Symposium on Performance Analysis of Systems and Software (ISPASS), pages 154–162, Austin, TX, Apr. 2000.



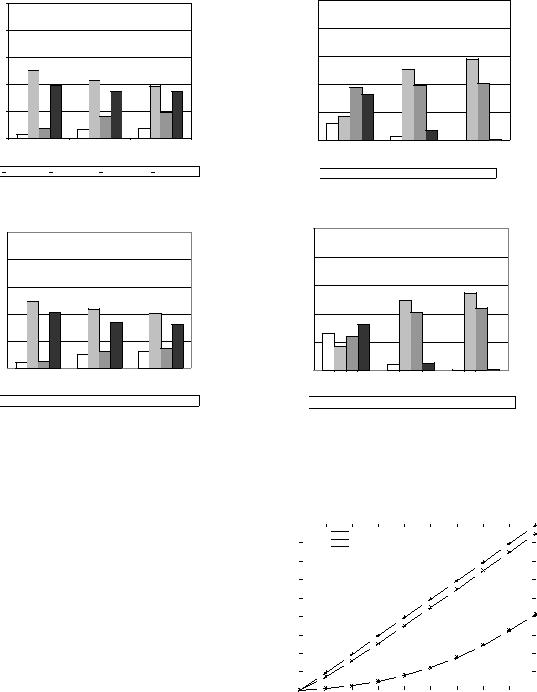


 avg. proc. time
avg. proc. time 
 avg. mem. time
avg. mem. time 
 avg. comm. time
avg. comm. time 
 avg. sync. time
avg. sync. time

 avg. proc. time
avg. proc. time  avg. mem. time
avg. mem. time  avg. comm. time
avg. comm. time  avg. sync. time
avg. sync. time

 avg. proc. time
avg. proc. time  avg. mem. time
avg. mem. time  avg. sync. time
avg. sync. time  avg. comm. time
avg. comm. time

 avg. proc. time
avg. proc. time 
 avg. mem. time
avg. mem. time 
 avg. sync. time
avg. sync. time 
 avg. comm. time
avg. comm. time