Аннотация
Раскрывается новое направление в теории транспортных потоков, теоретический аппарат которого позволяет описывать изменение состояний транспортного потока в дифференциальной форме, определять причинно-следственные связи. Движение потока автомобилей описывается как непрерывное изменение его состояний: разгона, равномерного движения, торможения.
Ключевые слова:
транспортный поток, интенсивность, скорость, плотность, ко-личество потока, инерционность, напряженность, транспортное время, путь.
Введение
Теория транспортного потока – наука, т.к. использует научный метод для получения соответствующих знаний и отличается от других наук предметом исследований. Она изучает явления, связанные с функционированием транспортных потоков, в том аспекте, который не раскрывается другими науками. Теория транспортных потоков является высшей формой организации знаний законов движения автомобилей в различных дорожных условиях, при разном уровне управления движением и в различных по составу транспортных потоках. Существующая теория транспортного потока не обладает в необходимой мере признаками адекватности и полноты отображения объективной реальности движения непрерывного насыщенного транспортного потока, т.к. результаты, получаемые на языке теории, описывают далеко не все возможные ситуации движения потока и автомобилей в потоке при различной дорожной обстановке в городах.
Публикаций по данному направлению на сегодняшний день нет.
Цель и постановка задачи
Рассмотрение систематизированных моделей с позиции составлении уравнений движения транс-портного потока во времени и в пространстве показывает, что уравнения движения, согласно общефизическим требованиям, должны включать ускорение, скорость и координаты потока [2,3] (или автомобилей потока), и позволяет сделать вывод, что таких уравнений фактически нет. Формально достаточно близкими к таким уравнениям являются уравнения упрощенной динамической модели и уравнения следования за лидером для описания движения одиночного автомобиля в квазипотоке. Описание движения транспортного потока заканчивается попыткой приспособить гидродинамическую аналогию уравнения неразрывности потока, состоящее из ускорения и распределения плотности в какой-либо точке пространства или в какой-либо момент времени [1-3]. Следовательно, дальнейшее формирование теории транспортного потока выполним в качественном направлении, т.к. стохастические зависимости не позволяют раскрыть причинно-следственные связи, закономерности, нелинейности и структуру транспортного поток. Новое направление в формировании теории не замыкается на качественной стороне динамики транспортного процесса, а представляет собой синтез накопленных знаний и экспериментальных данных с новыми законами и понятиями.
Решение задачи
Применение топологических методов для анализа системы «транспортный поток» требует определения основных экстенсивных и интенсивных параметров. Как было замечено рядом авторов [1-3], цепи и системы необходимо анализировать, используя продольные и поперечные переменные. В этом случае сопротивление движению и плотность транспортного потока определяются как отношения продольных и поперечных переменных [2-3]. Для определения указанных переменных выделим структурный элемент улично-дорожной сети, на котором возможно накопление единиц транспортного потока, их движение, уменьшение или увеличение скорости, возникновение заторов. Таким топологическим структурным элементом улично-дорожной сети является перегон (расстояние между перекрестками) единичной длины. Определим для любого перегона алгебраическое уравнение, связывающее скорость транспортного потока V и его интенсивность N. При этом учтем, что как скорость, так и интенсивность изменяются во времени, и поэтому используем символы V(t) и N(t).
Oписание характеристик перегона будет полным, если будут получены уравнения, связывающее переменные V(t) и N(t), которые характеризуют дуальность транспортной единицы в обобщенных параметрах.
Для получения обобщенных параметров, согласно методике [3], рассмотрим отношение V(t) и N(t), произведение V(t) и N(t) и быстроту изменения одной величины от другой во времени, т.е. первые производные по dt.
Предположим, что связь между V(t) и N(t) аппроксимируется прямой, проходящей через начало координат. Это предположение справедливо для условий насыщенного движения, когда с интенсивностью падает и скорость движения, доходя при заторе в своих значениях до нулей (N = 0; V = 0).
Уравнение, характеризующее отношение N(t) и V(t), можно записать как

где Q – обобщенный параметр, определяемый как быстрота изменения скорости транспортного потока при изменении интенсивности потока. Данный параметр Q известен как плотность транспортного потока, а уравнение (1) известно как основное уравнение состояния транспортного потока.

Размерность плотности – авт/км. Уравнение, свя-зывающее скорость V(t) и интенсивность N(t) как отношение, позволяет определить сопротивление движению транспортнoго потока по полосам перегона, возникающее с ростом плотности. В то же время уравнение, связывающее N(t) и V(t) как произведение, позволяет определить обобщенную мощность системы «транспортный поток – дорога»

или скорость изменения энергии потока [3], которую определим, учитывая (3), как «объем движения». Учитывая (1) и (2), получим
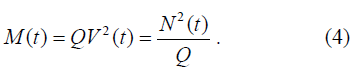
Из уравнения (4) следует, что объем движения на выходе перегона под влиянием плотности Q будет уменьшаться по сравнению со входом.
Рассмотрим теперь зависимость между продольной V(t) и поперечной N(t) переменными для задач, где V(t) – функция, N(t) – аргумент. Как и ранее, будем рассматривать линейную зависимость, позволяющую более просто получить и проанализировать обобщенные параметры системы «транспортный поток». Уравнение, характеризующее отношение V(t) и N(t), будет иметь вид

где S = 1/Q инверсионная плотность, представляющая собой долю пути, приходящуюся на один автомобиль потока, или быстроту изменения скороcти при изменении интенсивности. Фактически параметр S для плотных транспортных потоков представляет величину динамического габарита. Для движения насыщенного транспортного потока параметр S определим, как «динамический габарит», а для условий движения неплотных потоков – как «свободный динамический габарит», т.к. в этих случаях автомобилям обеспечивается свобода движения и отсутствует их взаимное влияние. С учетом динамического габарита объем движения транспортного потока определяется следующим уравнением:
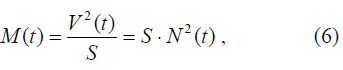
которое указывает, что с увеличением расстояния между автомобилями, т.е. динамического габарита, объем движения транспортного потока будет увеличиваться. Размерность и физический смысл параметра «объем движения» отличается от аналогичного термина в [1-2], где он больше соответствует термину «количество потока». В общефизическом понимании мощность всегда связана с общей энергией системы тождеством [3]

Учтем это тождество как основополагающее для описания движения транспортного потока.
Рассмотрим далее характеристики, для которых скорость потока V(t) является функцией, производной от интенсивности N(t) по времени, т.е. от быстроты изменения интенсивности. Аппроксимируем данную характеристику прямой, проходящей через начало координат, и получим уравнение вида
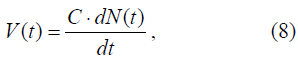
где С назовем «обобщенной напряженностью» транспортного потока, учитывающей быстроту уменьшения или увеличения расстояния между автомобилями.
Напряженность потока С характеризует собой быстроту изменения скорости при изменении интенсивности транспортного потока. Уравнение (8) представляет V(t) как явную функцию от интенсивности N(t). Для того чтобы определить имеющие практический интерес изменения интенсивности в зависимости от изменения скорости и образования в процессе движения групп, очередей, колонн, установим зависимость N(t) от V(t) в явном виде. Если ()dNt/dt существует, то обратное соотношение получим, проинтегрировав выражение (8):

Если N(t) – разрывная (ступенчатая) функция, то dN(t)/dt не существует, и уравнение (8) не является удовлетворительной формой уравнения напряженности, т.к. не имеет решения. Поэтому произведем замену переменных, введя новую переменную L(t) как обобщенное смещение (путь). Известно, что L(t) есть интеграл от скорости транспортного потокa, поэтому скорость есть непрерывная функция времени. Учитывая (8) и то, что аппроксимируемая прямая проходит через начало координат, получим уравнение для вариации относительно точки N(t) = 0

или для нелинейного случая

Следовательно, закон сжатия в группу, колонну или увеличения напряженности в транспортном потоке на перегоне можно выразить одной из следующих четырех формул:

которые указывают на накопление потенциала в потоке. Размерность напряженности – км*ч/авт.. Для получения следующего обобщенного параметра рассмотрим на однополосном перегоне зависимость временной производной скорости V(t) от интенсивности N(t), т.е. обратную зависимость по отношению к (8). Взаимосвязь N(t) с ()dVt/dt получим, также аппроксимируя характеристику этой связи при помощи прямой и направляя ее через начало координат. Получим уравнение вида
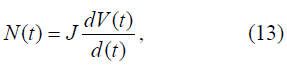
где J – передаточная функция инерционности автомобиля для рассматриваемой системы «транспортный поток». Интерпретируем ее как инерционность, т.е. как аккумулятор кинетического потенциала. В уравнении (13) интенсивность N(t) является явной функцией от ()dVt/dt. Если dVt)/dt существует в интервале 0 ? Т ? t, то решение уравнения имеет вид
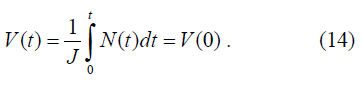
Если V(t) – разрывная функция, то уравнение (14) не имеет решения. Как и в случае с напряженностью, обойдем эту трудность, используя новую переменную q(t), названную «количеством потока» [2] и равную

Тогда
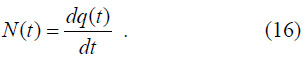
Если интенсивность является непрерывной функцией времени, то количество потока q(t) связано с интенсивностью N(t) соотношением
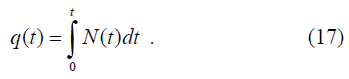
Произведение интенсивности потока на промежуток времени dt будет представлять элементарную величину интенсивности (увеличение на одну автомашину) n = Nd. В то же время произведение инерционности транспортного потока на скорость будет представлять собой количество потока q, и, следовательно, инерционность характеризует быстроту изменения количества потока (автомобилей) с изменением скорости потока q = JV .
Фактически элементарная величина интенсивности за время dt равна изменению количества потока за то же время dt, т.е.

Уравнение (18) указывает на закон изменения количества транспортного потока: «Изменение интенсивности транспортного потока за некоторый промежуток времени равно изменению количества автомобилей в потоке за то же время». Этот закон позволяет по начальной скорости автомобилей V*Q и известному количеству потока (величина, на которую изменилась интенсивность) находить конечную скорость автомобилей в потоке, минуя все вычисления промежуточных скоростей Vі. Количество транспортного потока представляет собой движущуюся группу, или «пачку», автомобилей на одной полосе, число которых в «пачке» может изменяться от одного автомобиля до некоторого максимального количества и, в свою очередь, зависит от протяженности участка дороги dl, где изучается движение транспортного потока, и от величины интервала времени dt. Закон сохранения количества потока возникает в связи с однородностью пространства дороги. В силу этой однородности свойства системы «транспортный поток» не будут меняться при любом параллельном переносе системы как целого в пространстве. Для исследуемой системы закон сохранения количества потока подтверждается тем обстоятельством, что при неизменной интенсивности N (приращение интенсивность равно нулю) количество потока будет величиной постоянной. Так, количество автомобилей в движущейся группе будет неизменным как на участке дороги L, так и на участке L + dl. Из уравнения (17) видно, что количество потока обладает важным свойством – аддитивностью. А именно, значение «количество потока» для транспортного потока, состоящего из автомобилей, взаимодействием которых можно пренебречь, равно сумме значений из каждого автомобиля в отдельности. Данное обстоятельство указывает на то, что в ка-честве количества потока можно рассматривать как один автомобиль, так и группу автомобилей. Уравнение (17) является основным уравнением количества потока и позволяет решать две типич-ные задачи: по известной величине интенсивности найти закон изменения количества в потоке или по известному закону изменения количества найти интенсивность потока. В то же время инерционность транспортного потока (13) характеризует аккумуляцию кинетического потенциала транспортного потока на полосе перегона при движении группы, «пачки» автомобилей, с максимальной скоростью после остановки у светофора. Численное значение инерционности можно получить из графической линейной зависимости q(t) от V(t), q(t) = J*V(t). Размерность инерционности J – авт.ч/км. Таким образом, накопление кинетического потенциала транспортного потока на перегоне будет описываться одним из следующих уравнений:

Обратная величина инерционности J представляет собой весьма интересный с позиции безопас-ности дорожного движения параметр – это быстрота изменения расстояния или динамического габарита автомобиля. Этот параметр характеризует ускоренность транспортного потока 1/J=В, единица измерения – км/авт*ч. Полученные уравнения транспортного потока, связывающие V(t), N(t) (3) и одно из уравнений состояния потока (1), (8), (13), (17) и характеризующие элемент системы «транспортный поток» позволяют определить энергетические показатели и, следовательно, составить уравнения движения транспортного потока во времени и в пространстве. Отношение q(t) к L(t) представляет собой плотность транспортно-го потока Q(t) = q(t)/L(t), а отношение L(t) к q(t) – динамический габарит St=Lt/qt. Данные характеристики транспортного потока рассмотрены выше. Таким образом, в основных транспортных характеристиках зависимость скорости от интенсивности описывается следующими уравнениями:
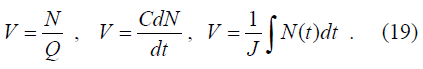
В свою очередь зависимость интенсивности от скорости

что аналогично общим законам моделирования систем [3].
Выводы
Используя общесистемные методы идентификации потоковых систем, установлены дорожный и транспортный потенциалы, эксергия – как внешняя работоспособность системы «транспортный поток – дорога» и определены три вида сопротивлений: плотность, инерционность и напряженность, которые позволяют составлять дифференциальные уравнения движения потока как через сечение, так и по перегону.
Список источников
- Хейт Ф. Математическая теория транспортных потоков / Пер. с англ. – М.: Мир, 1966. – 284 с.
- Гук В.И. Элементы теории транспортных пото-ков и проектирования улиц и дорог: Учеб. пособ. – К.: УМК ВО, 1991. – 254 с.
- Паллен К.Л. Топологические и матричные ме-тоды. Теория и применение / Пер. с англ. –М. – Л.: Энергия, 1966. – 98 с.