В настоящей работе рассматривается проблема распознавания шахматного лабиринта с помощью коллектив автоматов.
Исследования в данной теме ведутся с середины прошлого века [1]. Задача анализа для автоматов и лабиринтов изучалась в работах многих авторов. Одной из первых наиболее значимых работ стала «Мышь в лабиринте» К. Шеннона в 1952 году. На сегодняшний день остается множество нерешенных задач в данной области. Многие проблемы взаимодействия моделирования операционных сред сводятся к задаче распознавания графа.
Исходными данными является неизвестный шахматный лабиринт. Требуется построить алгоритм работы АИ и АЭ, позволяющий распознать этот лабиринт в виде комплекса прямоугольных областей.
Под шахматным лабиринтом понимается плоский неориентированный конечный связный граф G = (VG , EG) без дыр и мостов, множество вершин которого VG есть подмножество множества Z2 точек декартовой плоскости с целочисленными координатами, а множество ребер EG обладает следующим свойством: две любые вершины могут быть соединены ребром только тогда, когда расстояние между ними равно единице [2].
Для распознавания используется коллектив автоматов, состоящий из автомата-исследователя (АИ) и автомата-экспериментатора (АЭ).
АИ обходит граф по периметру и передает данные о своем движении АЭ. АИ имеет один камень. Он может воспринимать и анализировать информацию об 1 окрестности вершины, в которой он находится, помечать вершину камнем и снимать пометку. АИ может передвигаться по ребрам графа в четырех направлениях.
Ниже приведен алгоритм обхода АИ шахматного лабиринта по периметру.
1. АИ помещается на произвольную вершину графа.
2. АИ доходит до крайней левой вершины.
3. АИ доходит до крайней верхней вершины. АИ достиг внешнего левого верхнего угла.
4. АИ помечает вершину камнем.
5. АИ делает шаг вправо (в направлении а).
6. Если в текущей вершине доступно 3 направления движения, то переход к п.7, иначе переход к п.8.
7. АИ делает один шаг в том же направлении. Переход к п.11.
8. Если в текущей вершине доступно 2 направления движения, то переход к п.9, иначе переход к п.10.
9. АИ выбирает крайнее правое направление. Переход к п.11.
10. Доступно 4 направления. АИ выбирает крайнее левое направление. Переход к п.11.
11. Данные о направлении передаются АЭ.
12. Если вершина помечена камнем, то переход к п.13, иначе переход к п.6.
13. АИ передает АЭ информацию о завершении работы.
Ёмкостная и временная сложности распознавания составляют, где n и m – длина и ширина наименьшего прямоугольника, описанного вокруг лабиринта.
АЭ составляет выражение, описывающее движение АИ по ребрам графа. Затем АЭ обрабатывает полученное выражение, пошагово выделяя в нем прямоугольные структуры.
Ниже приведен алгоритм составления формулы, описывающей граф с помощью прямоугольников.
1. АЭ получает данные о шаге от АИ.
2. АЭ заносит данные о перемещении АИ в выражение.
3. Если АЭ получил информацию о завершении работы АИ, то переход к п.4, иначе переход к п.1.
4. На основании первого, второго и последнего элемента выражения АЭ выделяет прямоугольник.
5. Использованные элементы удаляются из выражения.
6. Если первый, второй и последний элементы имеют одинаковое направление, то они объединяются и переносятся в первую позицию.
7. На основании первого, второго и последнего элемента выражения АЭ выделяет прямоугольник и определяет его сдвиг относительно предыдущего.
8. Использованные элементы удаляются из выражения.
9. Если первый, второй и последний элементы имеют одинаковое направление, то они объединяются и переносятся в первую позицию.
10. Если исходное выражение пустое, то работа алгоритма завершена, иначе переход к п.7.
Доказана корректность приведенных алгоритмов. Алгоритм обхода лабиринта по внешнему контуру заканчивает свою работу, когда АИ достигает вершины, помеченной камнем. Алгоритм составления формулы заканчивается, когда из выражения, описывающего перемещение АИ, удалены все элементы. Полученная формула описывает шахматный лабиринт с точностью до изоморфизма.
Рассмотрим пример работы алгоритма. Задан шахматный лабиринт (см. рис. 1).
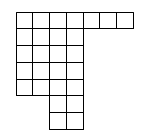
Рисунок 1 - Шахматный лабиринт для распознавания
После завершения работы АИ, АЭ составит выражение, описывающее перемещение АИ по внешнему периметру лабиринта, следующего вида:
7a+1(-b)+3(-a)+6(-b)+2(-a)+2b+2(-a)+5b
В результате обработки данного выражения будет получена формула:
(П(7,1)Сн(0,П(4,4)))Сн(2,П(2,2))
Новизна работы заключается в том, что результат распознавания представляется в виде формулы, описывающей лабиринт с помощью структуры прямоугольников и их расположения относительно друг друга.
Список использованной литературы
1. Кудрявцев В.Б. Автоматы в лабиринтах / В.Б. Кудряв-цев, Г. Килибарда. Ш. Ушумлич // Материалы IX Меж-дународной конференции
«Интеллектуальные системы и компьютерные науки» (23-27 октября 2006 г.). – М. : Издательство механико-математического факультета МГУ. – Т. 1, ч. 1. – С. 159-163.
2. Грунская В.И. О поведении автоматов в лабиринтах / В.И. Грунская // Материалы VIII Международного семинара «Дискретная математика и ее приложения»
(2-6 февраля 2004 г.). – М. : Издательство механико-математического факультета МГУ, 2004. – С. 264-267.