Аннотация
Л.А. Терейковская Марковские модели прогнозирования эксплуатационных параметров компьютерных сетей. Разработаны марковские модели, позволяющие прогнозировать значения эксплуатационных параметров компьютерных сетей на нестационарных режимах функционирования. Особенностью разработанных моделей является расчет параметров на основании результатов вейвлет–анализа динамики эксплуатационных параметров. Указаны пути усовершенствования модели.
Ключевые слова: компьютерная сеть, марковская модель, марковская цепь, переходные вероятности, нестационарный процесс, прогнозирование, вейвлет–анализ.
Постановка проблемы
Современные процессы информационной глобализации общества, стремительное возрастание уровня интеграции различных общественных, промышленных, научных и образовательных структур формируют необходимость повышения эффективности функционирования компьютерных сетей, которое уже не может быть достигнуто за счет применяемого программно-аппаратного обеспечения. Одним из основных направлений усовершенствования указанного программно–аппаратного обеспечения является разработка новых методов и моделей, на основании которых формируется прогноз значений их эксплуатационных параметров [1, 3, 4]. Отметим, что сформированный прогноз является базой как для планирования сетевых ресурсов, так и для определения оперативных управляющих воздействий на них. Таким образом, эффективность функционирования компьютерных сетей непосредственно зависит от достоверности методов и моделей прогноза эксплуатационных параметров, разработка которых и является общей проблемой настоящей статьи.
Анализ последних достижений и публикаций
Трудности разработки достоверных методов и моделей прогноза значений эксплуатационных параметров компьютерных сетей в основном связаны со сложным характером соответствующих статистических данных.
Известные модели прогноза, базирующиеся на использовании методов искусственного интеллекта включая теорию искусственного иммунитета, не позволяют явно рассчитать ожидаемую величину параметра, а лишь указывают на его принадлежность к какой-либо заранее определенной области. Еще одним общим недостатком подобных моделей является недостаточная надежность математического аппарата. Согласно работы [3], в современных условиях более перспективными являются модели, базирующиеся на теории марковских процессов. В марковских моделях исследуемый процесс апроксимируется с помощью марковской цепи, параметры которой рассчитываются на основании соответствующих статистических данных. При этом, многопериодический характер динамики параметров учитывается за счет нестационарности параметров марковской цепи. Так, в [3] разработана методика построения нестационарной марковской модели, параметры которой рассчитывались с использованием спектрального анализа данных методом Фурье. Заметим, что спектральный анализ данных методом Фурье позволяет рассчитать спектр исследуемого процесса, но не позволяет определить моменты возникновения/исчезновения частот. Таким образом, марковская модель [3], не позволяет адекватно прогнозировать процессы с нестационарным многопериодическим характером. Возможным путем устранения этого недостатка является спектральный анализ данных методом вейвлет–преобразований, позволяющий рассчитать частотно-временные характеристики исследуемого процесса.
Формулировка цели статьи
Разработка марковской модели, позволяющей прогнозировать значения эксплуатационных параметров компьютерных сетей на нестационарных режимах функционирования.
Изложение основного материала исследований
Случайный процесс изменения состояний некоторой системы называют марковской цепью (марковским процессом), если для произвольного момента времени вероятность перехода системы в новое состояние pі,j зависит только от текущего состояния системы Si и не зависит от того каким образом система попала в текущее состояние: pi,j = f (Si).
Для определения марковской цепи необходимо указать следующие параметры: вероятности переходов системы между состояниями за один шаг процесса (pi,j); количество (N) и признаки состояний, в которые может попасть подопытная система; вероятности пребывания системы по состояниям в нулевой момент времени (Pi(0)). При этом должно выполняться условие нормировки
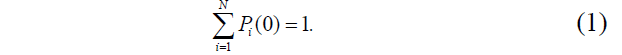
Заметим, что при исследовании изменения системы во времени пользуются не переходными вероятностями, а интенсивностями переходов. Указанные интенсивности представляют собой вероятности переходов между состояниями за единицу времени и рассчитываются так

Общепринято отображать марковскую цепь в виде размеченного графа, пример которого показан на рис. 1. Вершинам графа отвечают состояния марковской цепи, а дугам — возможные переходы между состояниями.
Количество и признаки состояний марковской цепи определяют исходя из условий задачи.
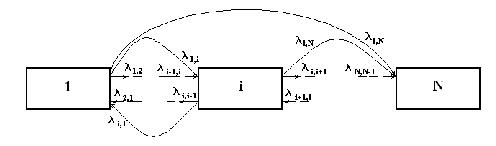
Рисунок 1 — Пример графа марковской цепи
В случае аппроксимации динамики эксплуатационных параметров компьютерных сетей рекомендуется, чтобы состояния с номерами от 1 до (N–1) соответствовали таким величинами параметров, при которых программно–аппаратное обеспечение сети будет находиться в работоспособном состоянии, а N–е состояние соответствовало неработоспособному состоянию [3]. При односторонней области работоспособности первые (N–1) состояния будут определяться нижними и верхними границами, а последнее N состояние — только нижней границей. Используя процедуру равномерного квантования области работоспособности, границы состояний определяются так
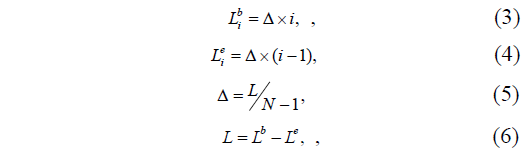
где 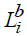 ,
, 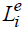 — верхняя и нижняя граница i–го состояния,
— верхняя и нижняя граница i–го состояния,  — ширина
кванта., L — ширина области работоспособности,
— ширина
кванта., L — ширина области работоспособности,  — верхний и нижний пределы области работоспособности. Иллюстрацией квантования является
рис. 2, на котором показаны графики реализаций некоторого эксплуатационного параметра
— верхний и нижний пределы области работоспособности. Иллюстрацией квантования является
рис. 2, на котором показаны графики реализаций некоторого эксплуатационного параметра 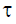 для однотипных объектов.
для однотипных объектов.

Рисунок 2 — Графики реализаций эксплуатационных параметров для однотипных объектов
Если параметры марковской цепи не зависят от времени — ее называют гомогенной, в противном случае говорят о негомогенных цепях. Определение параметров марковской цепи позволяет рассчитать вероятности пребывания процесса в каждом из состояний в произвольный момент времени.
Базовый вариант расчета подразумевает гомогенную цепь, интенсивности переходов которой рассчитываются так:
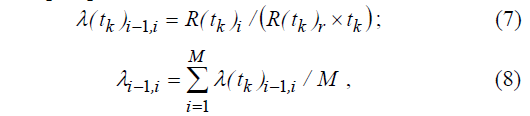
Для гомогенной марковской цепи расчет вероятностей пребывания реализуется с использованием системы уравнений Колмогорова–Чепмена вида:
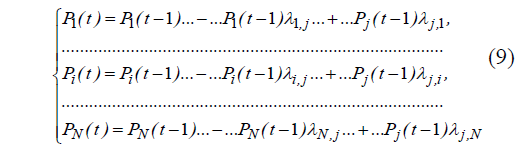
В расчетах (7) следует принимать во внимание начальные условия моделирования, определенные (1), а также условие нормировки:

Существенным недостатком гомогенной марковской модели (1–10) является возможность применения только монотонно возрастающих или убывающих параметров. В случае ярко выраженной многопериодической динамики параметров, характерной для компьютерных сетей, необходимо использовать негомогенные марковские модели. В соответствии с рекомендациями [3] негомогенная марковская модель может представлять собой совокупность гомогенных марковских цепей, каждая из которых должна аппроксимировать процесс на одном из монотонных участков (полупериодов). Точки, в которых наблюдается изменение периодичности процесса, будем называть переходными точками.
В простейшем случае, для однопериодического процесса, график которого показан на рис. 3, модель будет состоять из двух гомогенных марковских цепей. Первая цепь предназначена для моделирования участка АВ, вторая — для участка ВС. При этом, величины вероятностей пребывания первой марковской цепи в момент времени В, являются начальным распределением вида (1) для второй марковской цепи.
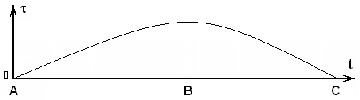
Рисунок 3 — График однопериодического процесса
Для двухпериодического процесса, график которого показан на рис. 4, марковская модель будет более сложной.
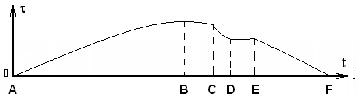
Рисунок 4 — График двухпериодического процесса
Сложность заключается в моделировании участка BF, который является нестационарным только на СЕ. При этом полупериоды CD и DE являются вложенными в полупериод BF. Рассмотрим возможные методы построения марковской модели.
Первый метод построения, по аналогии с однопериодическим процессом, будет заключаться в последовательном моделировании каждого из стационарных интервалов АВ, BC, CD, DE и EF своей гомогенной марковской цепью. Как и для предыдущего примера, конечное распределение вероятностей пребывания предыдущей марковской цепи является начальными условиями для последующей цепи. Кроме этого марковские цепи могут отличаться количеством и границами состояний, а также величинами интенсивностей переходов. Количество состояний и их границы следует выбирать исходя из требуемой точности моделирования. Рассчитать величины интенсивностей переходов необходимо по аналогии с (7), (8) отдельно для каждой марковской цепи, несколько модифицировав выражения для обработки статистики на соответствующем интервале функционирования (полупериоде)
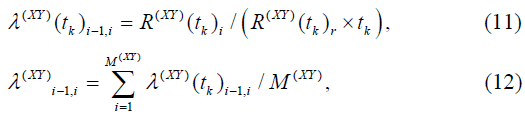
где XY – рассматриваемый полупериод.
Остальные обозначения (11), (12) соответствуют выражениям (7), (8).
Результирующую последовательную модель 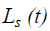 можно записать в виде:
можно записать в виде:

В компактном виде (13) можно записать так:
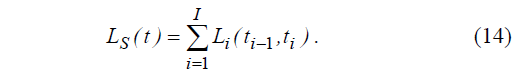
Однако, несмотря на простоту и наглядность, представленный метод имеет существенный недостаток — результирующая модель (14) не позволяет производить аппроксимацию процесса, удалив из него частотную составляющую, которой соответствует определенная марковская цепь. Таким образом, последовательная марковская модель не позволяет решать задачу фильтрации исследуемого процесса, которая имеет большое значение при прогнозировании значений функциональных параметров компьютерных сетей.
Второй метод построения заключается в разработке результирующей марковской модели, представляющей собой последовательную структуру, состоящую из гомогенных марковских цепей, каждая из которых предназначается для аппроксимации процесса на соответствующем полупериоде. При этом каждая гармоника моделируется двумя собственными марковскими цепями, переходные вероятности которых рассчитываются с учетом влияния на процесс параллельно функционирующих гармоник. Например, для двухпериодического процесса, график которого показан на рис. 5 на участке BF выделяются две гармоники. Полупериод первой гармоники совпадает с продолжительностью участка BF, а полупериоды второй гармоники равны интервалам CD и DE. Следуя методике построения модели при расчете интенсивностей перехода марковской цепи для BF к зарегистрированным значениям параметров процесса необходимо добавить значения гармоники соответствующей интервалу СЕ. При расчете интенсивностей перехода марковских цепей для CD и DE от зарегистрированных значений параметров процесса необходимо отнять значения гармоники соответствующей интервалу BF. Таким образом, параллельная модель для этого процесса будет состоять из четырех гомогенных марковских цепей, предназначенных для моделирования процесса на участках AB, BF, CD, и EF соответственно. Отметим, что рассчитать значения гармоник, из которых складывается процесс возможно используя методику обратного вейвлет–преобразования [2].
Результирующую параллельную модель можно записать в виде:
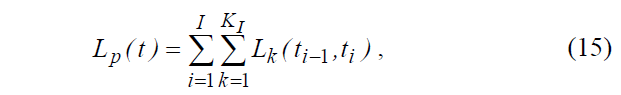
Модель (15) позволяет фильтровать подопытный процесс за счет удаления марковских цепей соответствующих определенным гармоникам. Ее недостатком относительно параллельной модели является более высокая вычислительная сложность, а в некоторых случаях, когда фильтрация не представляет интереса и избыточность.
Отметим, что для прогнозирования процесса на некотором интервале времени, необходимо определить какая периодичность отвечает этому интервалу и в моделях (14), (15) добавить соответствующие марковские цепи.
Очевидно, что достоверность разработанных марковских моделей непосредственно зависит от точности определения границ полупериодов и значений гармоник процесса. Для этого предлагается использовать методику проведения вейвлет–анализа динамики эксплуатационных параметров компьютерных сетей, разработанную автором и опубликованную в [2].
Выводы
Разработаны марковские модели, позволяющие проводить аппроксимацию, прогнозирование и фильтрацию динамики эксплуатационных параметров компьютерных сетей на нестационарных режимах.
Перспективы дальнейших исследований в данном направлении заключаются в четком определении сферы и условий использования разработанных моделей.
Список использованной литературы
1. Сыропятов А. А. Метод мониторинга трафика защищенных высокоскоростных коммерческих сетей нового поколения / А. А. Сыропятов // Наукові записки УНІДЗ. — 2009. — № 2(1) — С. 65–73.
2. Терейковская Л.А. Разработка статистической модели расчета периодических составляющих динамики функциональных параметров Internet-серверов / Л.А Терейковская // Управління розвитком складних систем: зб. наук. праць. — 2010. — Випуск 3. — С. 107–111.
3. Терейковский И.А. Моделирование профилей нормального поведения компьютерных систем / И. А. Терейковский // Защита информации: сб. науч. трудов НАУ. — 2006. — Выпуск 13. — С. 103–108.
4. Якубен М. Б. Обнаружение сетевых атак методом поиска аномалий на основе вероятностного и верификационного моделирования / М. Б. Якубен // Штучний інтелект. — 2005. — №3. — С. 679–687.