Назад в библиотеку

Простой итеративный алгоритм триангуляции Делоне

Авторы: А. В. Скворцов

В простом итеративном алгоритме поиск очередного треугольника реализуется следующим образом. Берётся любой треугольник, уже принадлежащий триангуляции (например, выбирается случайно), и последовательными переходами по связанным треугольникам ищется искомый треугольник.

При этом в худшем случае приходится пересекать все треугольники триангуляции, поэтому трудоемкость такого поиска составляет O(N).

Во многих практически важных случаях исходные точки не являются статистически независимыми, при этом точка i находится вблизи точки i+1. Поэтому в качестве начального треугольника для поиска можно брать треугольник, найденный ранее для предыдущей точки. Тем самым иногда удается достичь на некоторых видах исходных данных трудоемкости построения триангуляции в среднем O(N).

На практике обычно используются следующие способы поиска треугольника по заданной точке внутри него и по некоторому исходному треугольнику (рис. 1):

Варианты локализации треугольника в итеративных алгоритмах:

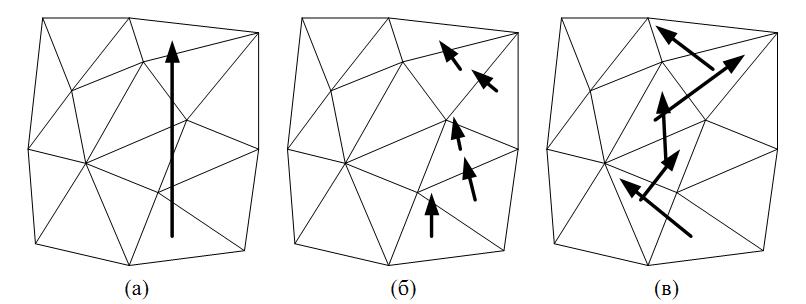
Рисунок 1 – Варианты локализации треугольника в итеративных алгоритмах: а – переходы вдоль прямой; б – переход через ближайшее к цели ребро; в – переход через разделяющее ребро

  1. Проводится прямая через некоторую точку внутри исходного треугольника и целевую точку, а затем нужно идти вдоль этой прямой к цели [1] (рис. 1, а). При этом необходимо корректно обрабатывать ситуации, когда на пути могут встретиться узлы и коллинеарные рёбра.
  2. Двигаться пошагово, на каждом шаге проводя прямую через центр текущего треугольника и целевую точку и затем переходя к соседнему треугольнику, соответствующему стороне, которую пересекает построенная прямая [2] (рис. 1, б).
  3. Двигаться пошагово, на каждом из которых надо переходить через такое ребро текущего треугольника, что целевая точка и вершина текущего треугольника, противолежащая выбираемому пересекаемому ребру, лежат по разные стороны от прямой, определяемой данным ребром [3, 4] (рис. 1, в). Этот способ обычно обеспечивает более длинный путь до цели, но он алгоритмически проще и поэтому быстрее.

Для правильной работы данного алгоритма поиска существенным является то, что в триангуляции выполняется условие Делоне. Если условие Делоне нарушено, то иногда возможно зацикливание алгоритма.

После того как требуемый треугольник найден, в нем строятся новые узел, рёбра и треугольники, а затем производится локальное перестроение триангуляции.

Литература

  1. Lawson C. Software for C surface interpolation // Mathematical Software III. NY: Academic Press. 1977. P. 161–194.
  2. Lee D., Schachter B. Two algorithms for constructing a Delaunay triangulation // Int. Jour. Comp. and Inf. Sc. 1980. Vol. 9. N. 3. P. 219–242.
  3. Скворцов А. В., Костюк Ю. Л. Эффективные алгоритмы построения триангуляции Делоне // Геоинформатика. Теория и практика. Вып. 1. Томск: Изд‑во Том. ун‑та, 1998. С. 22–47.
  4. Sloan S. W. A fast algorithm for constructing Delaunay triangulations in the plane // Adv. Eng. Software. 1987. Vol. 9. N. 1. P. 34–55.