Источник: https://www.cs.purdue.edu/homes/suresh/papers/cluster10.pdf

Asynchronous Algorithms in MapReduce

Karthik Kambatla, Naresh Rapolu, Suresh Jagannathan, Ananth Grama

Department of Computer Science, Purdue University {kkambatl, nrapolu, suresh, ayg}@cs.purdue.edu

Abstract—

Asynchronous algorithms have been demonstrated to improve scalability of a variety of applications in parallel environments. Their distributed adaptations have received relatively less attention, particularly in the context of conventional execution environments and associated overheads. One such framework, MapReduce, has emerged as a commonly used programming framework for large-scale distributed environments. While the MapReduce programming model has proved to be effective for data-parallel applications, significant questions relating to its performance and application scope remain unresolved. The strict synchronization between map and reduce phases limits expression of asynchrony and hence, does not readily support asynchronous algorithms.

This paper investigates the notion of partial synchronizations in iterative MapReduce applications to overcome global synchronization overheads. The proposed approach applies a locality-enhancing partition on the computation. Map tasks execute local computations with (relatively) frequent local synchronizations, with less frequent global synchronizations. This approach yields significant performance gains in distributed environments, even though their serial operation counts are higher. We demonstrate these performance gains on asynchronous algorithms for diverse applications, including PageRank, Shortest Path, and K-Means. We make the following specific contributions in the paper — (i) we motivate the need to extend MapReduce with constructs for asynchrony, (ii) we propose an API to facilitate partial synchronizations combined with eager scheduling and locality enhancing techniques, and (iii) demonstrate performance improvements from our proposed extensions through a variety of applications from different domains.

INTRODUCTION

Motivated by the large amounts of data generated by web-based applications, scientific experiments, business transactions, etc., and the need to analyze this data in effective, efficient, and scalable ways, there has been significant recent activity in developing suitable programming models, runtime systems, and development tools. The distributed nature of data sources, coupled with rapid advances in networking and storage technologies naturally motivate abstractions for supporting large-scale distributed applications.

Asynchronous algorithms have been shown to enhance the scalability of a variety of algorithms in parallel environments. In particular, a number of unstructured graph problems have been shown to utilize asynchrony effectively to tradeoff serial operation counts with communication costs. The increased communication costs in distributed settings further motivates the use of asynchronous algorithms. However, implementing asynchronous algorithms within traditional distributed computing frameworks presents challenges. These challenges, their solutions, and resulting performance gains form the focus of this paper.

To support large-scale distributed applications in unreliable wide-area environments, Dean and Ghemawat proposed a novel programming model based on maps and reduces, called MapReduce [4]. The inherent simplicity of this programming model, combined with underlying system support for scalable, fault-tolerant, distributed execution, make MapReduce an attractive platform for diverse data-intensive applications. Indeed, MapReduce has been used effectively in a wide variety of data processing applications. Large volumes of data processed at Google, Yahoo, Facebook, etc. stand testimony to the effectiveness and scalability of MapReduce. The open-source implementation of MapRe-duce, Hadoop MapReduce¹, serves as a development testbed for a wide variety of distributed data-processing applications.

A majority of the applications currently executing in the MapReduce framework have a data-parallel, uniform access profile, which makes them ideally suited to map and reduce abstractions. Recent research interest, however, has focused on more unstructured applications that do not lend themselves naturally to data-parallel formulations. Common examples of these include sparse unstructured graph operations (as encountered in diverse domains including social networks, financial transactions, and scientific datasets), discrete optimization and state-space search techniques (in business process optimization, planning), and discrete event modeling. For these applications, there are two major unresolved questions: (i) can the existing MapReduce framework effectively support such applications in a scalable manner? and (ii) what enhancements to the MapReduce framework would significantly enhance its performance and scalability without compromising desirable attributes of programmability and fault tolerance?

This paper primarily focuses on the second question

— namely, it seeks to extend the MapReduce semantics to support specific classes of unstructured applications on large-scale distributed environments. Recognizing that one of the key bottlenecks in supporting such applications is the global synchronization between the map and reduce

¹ Hadoop. http://hadoop.apache.org/mapreduce/ phases, it introduces notions of partial synchronization and eager scheduling. The underlying insight is that for an important class of applications, algorithms exist that do not need (frequent) global synchronization for correctness. Specifically, while global synchronizations optimize serial operation counts, violating these synchronizations merely increases operation counts without impacting correctness of the algorithm. Common examples of such algorithms include, computation of eigenvectors (pageranks) through (asynchronous) power methods, branch-and-bound based discrete optimization with lazy bound updates, computing all-pairs shortest paths in sparse graphs, constraint labeling and other heuristic state-space search algorithms. For such algorithms, a global synchronization can be replaced by concurrent partial synchronizations. However, these partial synchronizations must be augmented with suitable locality enhancing techniques to minimize their adverse effect on operation counts. These locality enhancing techniques typically take the form of min-cut graph partitioning and aggregation in graph analysis, periodic quality equalization in branch-and-bound, and other such operations that are well known in the parallel processing community. Replacing global synchronizations with partial synchronizations also allows us to schedule subsequent maps in an eager fashion. This has the important effect of smoothing load imbalances associated with typical applications.

This paper combines partial synchronizations, locality enhancement, and eager scheduling, along with algorithmic asynchrony to deliver distributed performance improvements of up to 800% (and beyond in some cases). Importantly, our proposed enhancements to programming semantics do not impact application programmability. We demonstrate all of our results on an Amazon EC2 8-node cluster, which involves real-world cloud latencies, in the context of PageRank, Shortest Path, and clustering (K-Means) implementations. These applications are selected because of their ubiquitous interaction patterns, and are representative of a broad set of application classes.

The rest of the paper is organized as follows: section II provides a more comprehensive background on MapReduce, Hadoop, and motivates the problem; section III outlines our primary contributions and their significance; section IV provides an API to realize partial synchronizations; section V discusses our implementations of the proposed API, PageRank, Shortest Path and K-Means clustering in the context of the API and analyze the performance gains of our approach. We outline avenues for ongoing work and conclusions in sections VIII and IX.

II. Background and Motivation

The primary design motivation for the functional MapRe-duce abstractions is to allow programmers to express simple concurrent computations, while hiding the cumbersome details of parallelization, fault-tolerance, data distribution, and load balancing in a single library [4]. The simplicity of the API makes programming easy. Programs in MapReduce are expressed as map and reduce operations. The map phase takes in a list of key-value pairs and applies the programmer-specified map function independently on each pair in the list. The reduce phase operates on a list, indexed by a key, of all corresponding values and applies the reduce function on the values; and outputs a list of key-value pairs. Each phase involves distributed execution of tasks (application of the user-defined functions on a part of the data). The reduce phase must wait for all the map tasks to complete, since it requires all the values corresponding to each key. In order to reduce the network overhead, a combiner is often used to aggregate over keys from map tasks executing on the same node. Fault tolerance is achieved through deterministic-replay, i.e., re-scheduling failed computations on another running node. Most applications require iterations of MapReduce jobs. Once the reduce phase terminates, the next set of map tasks can be scheduled. As may be expected, for many applications, the dominant overhead in the program is associated with the global synchronizations between the map and reduce phases. When executed in wide-area distributed environments, these synchronizations often incur substantial latencies associated with underlying network and storage infrastructure.

To alleviate the overhead of global synchronization, we propose partial synchronizations (synchronization only across a subset of maps) that take significantly less time depending on where the maps execute. We observe that in many parallel algorithms, frequent partial synchronizations can be used to reduce the number of global synchronizations. The resulting algorithm(s) may be suboptimal in serial operation counts, but can be more efficient and scalable in a MapReduce framework. A particularly relevant class of algorithms where such tradeoffs are possible are iterative techniques applied to unstructured problems (where the underlying data access patterns are unstructured). This broad class of algorithms underlies applications ranging from PageRank to sparse solvers in scientific computing applications, and clustering algorithms. Our proposed API incorporates a two-level scheme to realize partial synchronization in MapReduce, described in detail in section IV.

We illustrate the concept using a simple example — consider PageRank computations over a network, where the rank of a node is determined by the rank of its neighbors. In the traditional MapReduce formulation, during each iteration, map involves each node pushing its PageRank to all its outlinks and reduce accumulates all neighbors’ contributions to compute PageRank for the corresponding node. These iterations continue until the PageRanks converge. An alternate formulation would partition the graph; each map task now corresponds to the local PageRank computation of all nodes within the sub-graph (partition). For each of the internal nodes (nodes that have no edges leaving the partition), a partial reduction accurately computes the rank (assuming the neighbors’ ranks were accurate to begin with). On the other hand, boundary nodes (nodes that have edges leading to other partitions) require a global reduction to account for remote neighbors. It follows therefore that if the ranks of the boundary nodes were accurate, ranks of internal nodes can be computed simply through local iterations. Thus follows a two-level scheme, wherein partitions (maps) iterate on local data to convergence and then perform a global reduction. It is easy to see that this two-level scheme increases the serial operation count. Moreover, it increases the total number of synchronizations (partial + global) compared to the traditional formulation. However, and perhaps most importantly, it reduces the number of global reductions. Since this is the major overhead, the program has significantly better performance and scalability.

Indeed optimizations such as these have been explored in the context of traditional HPC platforms as well with some success. However, the difference in overhead between a partial and global synchronization in relation to the intervening useful computation is not as large for HPC platforms. Consequently, the performance improvement from algorithmic asynchrony is significantly amplified on distributed platforms. It also follows thereby that performance improvements from MapReduce deployments on wide-area platforms, as compared to single processor executions are not expected to be significant unless the problem is scaled significantly to amortize overheads. However, MapReduce formulations are motivated primarily by the distributed nature of underlying data and sources, as opposed to the need for parallel speedup. For this reason, performance comparisons must be with respect to traditional MapReduce formulations, as opposed to speedup and efficiency measures more often used in the parallel programming community. While our development efforts and validation results are in the context of PageRank, K-Means and Shortest Path algorithms, concepts of partial reductions combined with locality enhancing techniques and eager map scheduling apply to broad classes of iterative asynchronous algorithms.

III. Technical Contributions

This paper makes the following specific contributions —

•    Motivates the use of MapReduce for implementing asynchronous algorithms in a distributed setting.

•    Proposes partial synchronizations and an associated API to alleviate the overhead due to the expensive global synchronization between map and reduce phases. Global synchronizations limit asynchrony.

•    Demonstrates the use of partial synchronization and eager scheduling in combination with coarse-grained, locality enhancing techniques.

•    Evaluates the applicability and performance improvements due to the aforementioned techniques on a variety of applications - PageRank, Shortest Path, and K-Means.

IV. Proposed API

In this section, we present our API for the proposed partial synchronization and discuss its effectiveness. Our API is built on the rigorous semantics for iterative MapReduce, we propose in the associated technical report [7]. As mentioned earlier, our API for iterative MapReduce comprises a two-level scheme — local and global MapReduce. We refer to the regular MapReduce with global synchronizations as global MapReduce, and MapReduce with local/partial synchronization as local MapReduce. A global map takes a partition as input, and involves invocation of local map and local reduce functions iteratively on the partition. The local reduce operation applies the specified reduction function to only those key-value pairs emanating from local map functions. Since partial synchronization suffices, local map operations corresponding to the next iteration can be eagerly scheduled. The local map and local reduce operations can use a thread-pool to extract further parallelism.

Often, the local and global map/reduce operations are functionally the same and differ only in the data they are applied on. Given a regular MapReduce implementation, it is fairly straight-forward to generate the local map and local reduce functions using the semantics explained in the technical report [7], thus not increasing the programming complexity. In the traditional MapReduce API, the user provides map and reduce functions along with the functions to split and format the input data. To generate the local map and local reduce functions, the user must provide functions for termination of global and local MapReduce iterations, and functions to convert data into the formats required by the local map and local reduce functions.

However, to accommodate greater flexibility, we propose use of four functions — gmap, greduce, lmap and lreduce; gmap invoking lmap and lreduce functions, as described in section V. Functions Emit() and EmitIn-termediate() support data-flow in traditional MapReduce. We introduce their local equivalents — EmitLocal() and EmitLocalIntermediate(). Function lreduce operates on the data emitted through EmitLocalIntermediate(). At the end of local iterations, the output through EmitLocal() is sent to the greduce; otherwise, lmap receives it as input. Section V describes our implementation of the API and our implementations of PageRank, Shortest Path, and K-Means using the proposed API; demonstrating its ease of use and effectiveness in improving the performance of applications using asynchronous algorithms.

V. Implementation and evaluation

In this section, we describe our implementation of the API and the performance benefits from the proposed techniques of locality-enhanced partitioning, partial synchronization,

Table I

Measurement testbed, Software

and eager scheduling. We consider three applications — PageRank, Shortest Path, and K-Means to compare general MapReduce implementations with their modified implementations.

Our experiments were run on an 8-node Amazon EC2 cluster of extra large instances. This reflects the characteristics of a typical cloud environment. Also, it allows us to monitor the utilization and execution of map and reduce tasks. Table I presents the physical resources, software, and restrictions on the cluster.

A. API Implementation

As in regular MapReduce, our execution also involves map and reduce phases; each phase executing tasks on nodes. Each map/reduce task involves the application of gmap/greduce functions to corresponding data. Within the gmap function we execute local MapReduce iterations.

Figure 1. Construction of gmap from lmap and lreduce

Figure 1 describes our construction of gmap from the user-defined functions — lmap and lreduce. The argument to gmap is a <key, value> list(.v.v), on which the local MapReduce operates, lmap takes an element of .v.v as input, and emits its output by invoking EmitLocalIntermediate(). Once all the lmap functions execute, lreduce operates on the local intermediate data. A hashtable is used to store the intermediate and final results of the local MapReduce. Upon local convergence, gmap outputs the contents of this hashtable. greduce acts on gmap’s output. Such an implementation allows the use of other optimizations like combiners in conjunction. A combiner, as described in the original MapReduce paper [4], operates on the output of all gmap tasks on a single node to decrease the network traffic during the synchronization.

The rest of the section describes benchmark applications, their regular and eager (partial synchronization with eager scheduling) implementations, and corresponding performance gains. We discuss Page Rank in detail to illustrate our approach; Shortest Path and K-Means are discussed briefly in the interest of space.

B. PageRank

The PageRank of a node is the scaled sum of the PageR-anks of all its incoming neighbors, given by the following expression:

where x is the damping factor, s.pagerank and s.outlinks correspond to the PageRank and the out-degree of the source node, respectively.

The asynchronous PageRank algorithm involves an iterative two step method. In the first step, the PageRank of each node is sent to all its outlinks. In the second step, the PageRanks received at each node are aggregated to compute the new PageRank. The PageRanks change in each iteration, and eventually converge to the final PageRanks. For regular as well as eager implementations, we use a graph represented as adjacency lists as input. All nodes have an initial PageRank of 1. We define convergence by a bound on the norm of difference (infinite norm of I () in our case).

1) General PageRank: The general MapReduce implementation of PageRank iterates over a map task that emits the PageRanks of all the source nodes to the corresponding destinations in the graph, and a reduce task that accumulates PageRank contributions from various sources to a single destination. In the actual implementation, the map function emits tuples of the type < d_n,p_n >, where d_n is the destination-node, and p„ is the PageRank contributed to this destination node by the source. The reduce task operates on a destination node, gathering the PageRanks from the incoming source nodes and computes a new PageRank. After every iteration, the nodes have renewed PageRanks which propagate through the graph in subsequent iterations until they converge. One can observe that a small change in the PageRank of a single node is broadcast to all the nodes in the graph in successive iterations of MapReduce, incurring a potentially significant cost.

Our baseline for performance comparison is a MapReduce implementation for which maps operate on complete partitions, as opposed to single node adjacency lists. We use this as a baseline because the performance of this formulation was noted to be on par or better than the adjacency-list formulation. For this reason, our baseline provides a more competitive implementation.

2) Eager PageRank: We begin our description of Eager PageRank with an intuitive illustration of how the underlying algorithm accommodates asynchrony. In a graph with specific structure (say, a power-law type distribution), one may assume that each hub is surrounded by a large number of spokes, and that inter-component edges are relatively fewer. This allows us to relax strict synchronization on intercomponent edges until the sub-graph in the proximity of a hub has relatively self-consistent PageRanks. Disregarding the inter-component edges does not lead to algorithmic inconsistency since, after few local iterations of MapReduce calculating the PageRanks in the sub-graph, there is a global synchronization (following a global map), leading to a dissemination of the PageRanks in this sub-graph to other subgraphs via inter-component edges. This propagation imposes consistency on the global state. Consequently, we update only the (neighboring) nodes in the smaller sub-graph. We achieve this by a set of iterations of local MapReduce as described in the API implementation. This method leads to improved efficiency if each global map operates on a component or a group of topologically localized nodes. Such topology is inherent in the way we collect data as it is crawler-induced. One can also use one-time graph partitioning using tools like Metis². We use Metis since our test data set is not partitioned a-priori.

In the Eager PageRank implementation, the map task operates on a sub-graph. Local MapReduce, within the global map, computes the PageRank of the constituent nodes in the sub-graph. Hence, we run the local MapReduce to convergence. Instead of waiting for all the other global map tasks operating on different sub-graphs, we eagerly schedule the next local map and local reduce iterations on the individual sub-graph inside a single global map task. Upon local convergence on the sub-graphs, we synchronize globally, so that all nodes can propagate their computed PageRanks to other sub-graphs. This iteration over global MapReduce runs to convergence. Such an Eager PageR-ank incurs more computational cost, since local reductions may proceed with imprecise values of global PageRanks. However, the PageRank of any node propagated by the local reduce is representative, in a way, of the sub-graph it belongs to. Thus, one may observe that the local reduce and global reduce functions are functionally identical. As the sub-graphs (partitions) have approximately the same number of edges, we expect similar number of local iterations in each global map. However, if the convergence rates are very different, the global synchronization requires waiting for all partitions to converge.

Note that in Eager PageRank, local reduce waits on a local synchronization barrier, while the local maps can be implemented using a thread pool on a single host in a cluster. The local synchronization does not incur any inter-host

Table II

PageRank INPUT GRAPH PROPERTIES

communication delays. This makes associated overheads considerably lower than the global overheads.

3)    Input data: Table II describes the two graphs used as input for our experiments on PageRank, both conforming to power-law distributions. Graph A has 280K nodes and about 3 million edges. Graph B has 100K nodes and about 3 million edges. We use preferential attachment [3] to generate the graphs using igraph³. The algorithm used to create the synthetic graphs is described below, along with its justification.

Preferential attachment based graph generation.

Test graphs are generated by adding vertices one at a time — connecting them to numConn vertices already in the network, chosen uniformly at random. For each of these numConn vertices, numIn and numOut of its inlinks and outlinks are chosen uniformly at random and connected to the joining vertex. This is done for all the newly connected nodes to the incoming vertex. This method of creating a graph is closely related to the evolution of online communities, social networks, the web, etc. This procedure increases the probability of highly reputed nodes getting linked to new nodes, since they have greater likelihood of being in an inlink from other randomly chosen sites. The best-fit for inlinks in the two input graphs yields the power-law exponent for the graphs, demonstrating their conformity with the hubs-and-spokes model. Very few nodes have a very high inlink values, emphasizing our point that very few nodes require frequent global synchronization. More often than not, even these nodes (hubs) mostly have spokes as their neighbors.

Crawlers inherently induce locality in the graphs as they crawl neighborhoods before crawling remote sites. We partition graphs using Metis. A good partitioning algorithm that minimizes edge-cuts has the desired effect of reducing global synchronizations as well. This partitioning is performed off-line (only once) and takes about 5 seconds which is negligible compared to the runtime of PageRank, and hence is not included in the reported numbers.

4)    Results: To demonstrate the dependence of performance on global synchronizations, we vary the number of iterations of the algorithm by altering the number of partitions the graph is split into. Fewer partitions result in a smaller number of large sub-graphs. Each map task does more work and would normally result in fewer global

³The Igraph Library. http://igraph.sourceforge.net/

iterations in the relaxed case. The fundamental observation here is that it takes fewer iterations to converge for a graph having already converged sub-graphs. The trends are more pronounced when the graph follows the power-law distribution more closely. In either case, the total number of iterations are fewer than in the general case. For Eager PageRank, if the number of partitions is decreased to one, the entire graph is given to one global map and its local MapReduce would compute the final PageRanks of all the nodes. If the partition size is one, each partition gets a single adjacency list; Eager PageRank becomes General PageRank, because each map task operates on a single node.

Figure 4. PageRank: Time to converge(on y-axis) for various number of Partitions(on x-axis) for Graph A

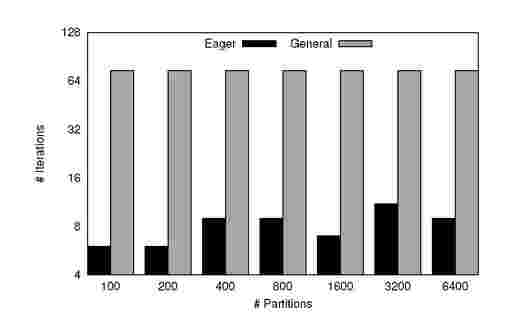
Figure 2. PageRank: Number of Iterations to converge(on y-axis) for different number of Partitions(on x-axis) for Graph A

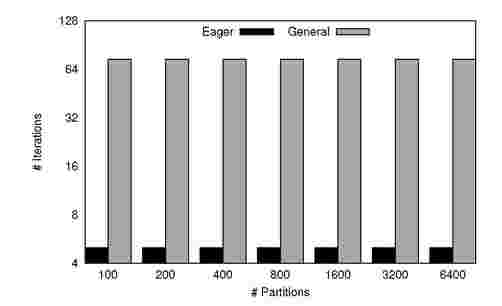
Figure 3. PageRank: Number of Iterations to converge(on y-axis) for different number of Partitions(on x-axis) for Graph B

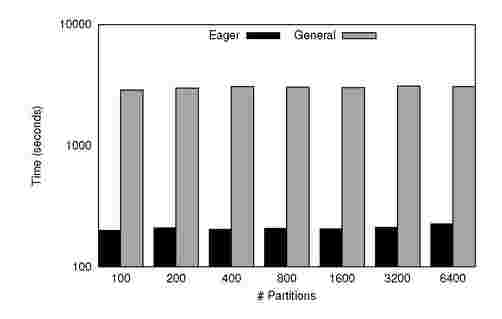
Figure 5. PageRank: Time to converge(on y-axis) for various number of Partitions(on x-axis) for Graph B

Figures 2 and 3 show the number of global iterations taken by the eager and general implementations of PageRank on input graphs A and B that we use for input, as we vary the number of partitions. The number of iterations does not change in the general case, since each iteration performs the same work irrespective of the number of partitions and partition sizes.

The results for Eager PageRank are consistent with our expectation. The number of global iterations is low for fewer partitions. However, it is not strictly monotonic since partitioning into different number of partitions results in varying number of inter-component edges.

The time to solution depends strongly on the number of iterations but is not completely determined by it. It is true that the global synchronization costs would decrease when we reduce the number of partitions significantly; however, the work to be done by each map task increases significantly. This increase potentially results in increased cost of computation, more so than the benefit of decreased communication. Hence, there exists an optimal number of partitions for which we observe best performance.

Figures 4 and 5 show the runtimes for the eager and general implementations of PageRank on graphs A and B with varying number of partitions. These figures highlight significant performance gains from the relaxed case over the general case for both graphs. On an average, we observe 8x improvement in running times.

C. Shortest Path

Shortest Path algorithms are used to compute the shortest paths and distances between nodes in directed graphs. The graphs are often large and distributed (for example, networks of financial transactions, citation graphs) and require computation of results in reasonable (interactive) times. For our evaluation, we consider Single Source Shortest Path algorithm in which we find the shortest distances to every node in the graph from a single source. All-Pairs Shortest Path has a related structure, and a similar approach can be used.

Distributed implementation of the commonly used Dijk-stra’s algorithm for Single Source Shortest Path allows asyn-chrony. The algorithm maintains the shortest known distance of each node in the graph from the source (initialized to zero for the source and infinity for the rest of the nodes). Shortest distances are updated for each node as and when a new path to the node is discovered. After a few iterations, all paths to all nodes in the graph are discovered, and hence the shortest distances converge. Distributed implementations of the algorithm allow partitioning of the graph into sub-graphs, and computing shortest distances of nodes using the paths within the sub-graph asynchronously. Once all the paths in the sub-graph are considered, a global synchronization is required to account for the edges across sub-graphs.

Figure 6. Single Source Shortest Path: Number of Iterations to converge(on y-axis) for different number of Partitions(on x-axis) for Graph A

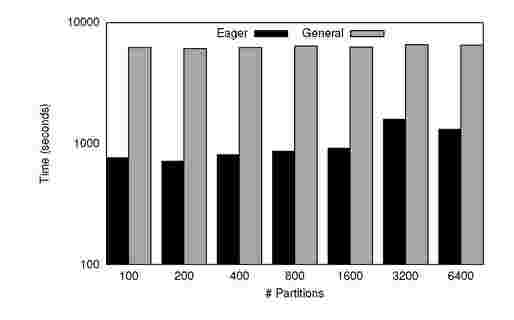
Figure 7. Single Source Shortest Path: Time to converge(on y-axis) for various number of Partitions(on x-axis) for Graph A

1)    Implementation: In the general implementation of Single Source Shortest Path in MapReduce, each map operates on one node, say u (would take its adjacency list as input); and for every destination node v, emits the sum of the shortest distance to u and the weight of the edge (u, j) in consideration. This is the shortest distance to the destination node v on a known path through the node n. Each reduce function operates on one node (receives weights of paths through multiple nodes as input); finds the minimum of the different paths to find the shortest path until that iteration. Convergence takes a number of iterations — the shortest distances of nodes from the source would not change for subsequent iterations. Again for the base case (like in PageRank), we take a partition as input instead of a single node’s adjacency list, without any loss in performance.

In the eager implementation of Single Source Shortest Path, each map takes a sub-graph as input; and through iterations of local map and local reduce functions, computes the shortest distances of nodes in the sub-graph from the source through other nodes in the same sub-graph. A global reduce ensues upon convergence of all local MapReduce operations. Since most real-world graphs are heavy-tailed, edges across partitions are rare and hence we expect a decrease in the number of global iterations, with bulk of the work performed in the local iterations.

2)    Results: We evaluate Single Source Shortest Path on graph A used in the evaluation of PageRank. We assign random weights to the edges in the graphs.

Figure 6 shows the number of global iterations (synchronizations) Single Source Shortest Path takes to converge for varying number of partitions in graph A. Clearly, the eager implementation requires fewer global iterations for fewer partitions. Again, the iteration count is not strictly monotonic, due to differences in partitioning. The number of global iterations in the general implementation remains the same.

Figure 7 shows the convergence time for Single Source Shortest Path for varying number of partitions in graph A. As observed in PageRank, though the running time depends on the number of global iterations, it is not entirely determined by it. As in the previous case, we observe significant performance improvements amounting to 8x speedup over the general implementation.

D. K-Means

K-Means is a commonly-used technique for unsupervised clustering. Implementation of the algorithm in the MapRe-duce framework is straightforward as outlined in [10, 2]. Briefly, in the map phase, every point chooses its closest cluster centroid and in the reduce phase, every centroid is updated to be the mean of all the points that chose the particular centroid. The iterations of map and reduce phases continue until the centroid movement is below a given threshold. Euclidean distance metric is usually used to calculate the centroid movement.

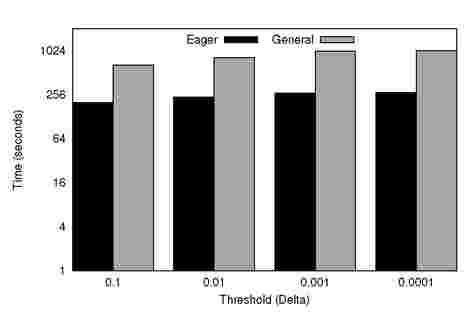
Figure 9. Time-to-Converge for Varying thresholds

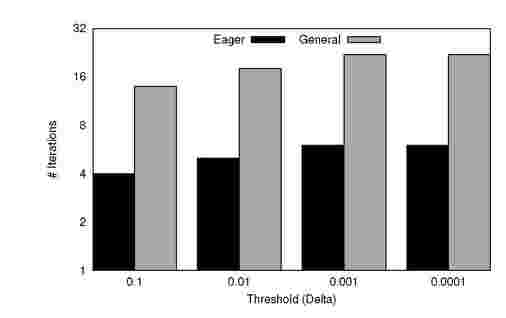
Figure 8. Iterations-to-Converge for Varying thresholds

In Eager K-Means, each global map handles a unique subset of the input points. The local map and local reduce iterations inside the global map, cluster the given subset of the points using the common input-cluster centroids. Once the local iterations converge, the global map emits the input-centroids and their associated updated-centroids. The global reduce calculates the final-centroids, which is the mean of all updated-centroids corresponding to a single input-centroid. The final-centroids form the input-centroids for the next iteration. These iterations continue until the input-centroids converge.

The algorithm used in the eager approach to K-Means is similar to the one recently proposed by Tom-Yov and Slonim [12] for pairwise clustering. An important observation from their results is that the input to the global map should not be the same subset of the input points in every iteration. Every few iterations, the input points need to be partitioned differently across global maps so as to avoid the algorithm’s move towards local optima. Also, the convergence condition includes detection of oscillations along with the Euclidean metric.

We use the K-Means implementation in the normal MapReduce framework from the Apache Mahout project³. Sampled US Census data of 1990 from the UCI Machine Learning repository⁴ is used as input for comparison between the general and eager approaches. The sample size is around 200K points each with 68 dimensions. For both General and Eager K-Means, initial centroids are chosen at random for the sake of generality. Algorithms such as canopy clustering can be used to identify initial centroids for faster execution and better quality of final clusters.

Figure 8 shows the number of iterations required to converge for different thresholds of convergence, with a fixed number of partitions (52). It is evident that it takes more iterations to converge for smaller threshold values. However, Eager K-Means converges in less than one-third of the global iterations taken by general K-Means. Figure 9 shows the time taken to converge for different thresholds. As expected, the time to converge is proportional to the number of iterations. It takes longer to converge for smaller threshold values. Partial synchronizations lead to a performance improvement of about 3.5x on average compared to general K-Means.

E. Broader Applicability

While we present results for only three applications, our approach is applicable to a broad set of applications that admit asynchronous algorithms. These applications include

— all-pairs shortest path, network flow and coding, neural-nets, linear and non-linear solvers, and constraint matching.

VI. DISCUSSION

We now discuss some important aspects of our results — primarily, (i) does our proposed approach generalize beyond small classes of applications? (ii) what impact does it have on the overall programmability? and (iii) how does it interact with other aspects, such as fault tolerance and scalability, of the underlying system?

Generality of Proposed Extensions. Our partial synchronization techniques can be generalized to broad classes of applications. PageRank, which relies on an asynchronous mat-vec, is representative of eigenvalue solvers (computing eigenvectors using the power method of repeated multiplications by a unitary matrix). Asynchronous mat-vecs form the core of iterative linear system solvers. Shortest Path represents a class of applications over sparse graphs that includes minimum spanning trees, transitive closure, and connected components. Graph alignment through random-walks and isoranks can be directly cast into our framework. A wide range of applications that rely on the spectra of a graph can be computed using this algorithmic template.

Our methods directly apply to neural-nets, network flow, and coding problems, etc. Asynchronous K-Means clustering immediately validates utility of our approach in various clustering and data-mining applications. The goal of this paper is to examine tradeoffs of serial operation counts and distributed performance. These tradeoffs manifest themselves in wide application classes.

Programming Complexity. While allowing partial synchronizations and relaxed global synchronizations requires slightly more programming effort than traditional MapRe-duce, we argue that the programming complexity is not substantial. This is manifested in the simplicity of the semantics in the technical report [7] and the API proposed in the paper. Our implementations of the benchmark problems did not require modifications of over tens of lines of MapReduce code.

Other Optimizations. Few optimizations have been proposed for MapReduce for specific cases. Partial synchronization techniques do not interfere with these optimizations. eg., Combiners are used to aggregate intermediate data corresponding to one key on a node so as to reduce the network traffic. Though it might seem our approach might interfere with the use of combiners, combiners are applied to the output of global map operations, and hence local reduce (part of the map) has no bearing on it.

Fault-tolerance. While our approach relies on existing MapReduce mechanisms for fault-tolerance, in the event of failure(s), our recovery times may be slightly longer, since each map task is coarser and re-execution would take longer. However, all of our results are reported on a production cloud environment, with real-life transient failures. This leads us to believe that the overhead is not significant.

Scalability. In general, it is difficult to estimate the resources available to, and used by a program executing in the cloud. In order to get a quantitative understanding of our scalability, we ran a few experiments on the 460-node cluster (provided by the IBM-Google consortium as part of the CluE NSF program) using larger data sets. Such high node utilization incurs heavy network delays during copying and merging before the reduce phase, leading to increased synchronization overheads. By showing significant performance improvements on a huge data set even in a setting of such large scale, our approach demonstrates scalability.

VII. Related work

Several research efforts have targeted various aspects of asynchronous algorithms. These include novel asynchronous algorithms for different problems [9, 1], analysis of their convergence properties, and their execution on different platforms with associated performance gains. Recently, it has been shown that asynchronous algorithms for iterative numerical kernels significantly enhance performance on multicore processors [8]. In shared-memory systems, apart from the reduced synchronization costs, reduction in the off-chip memory bandwidth pressure due to increased data locality is a major factor for performance gains. Though the execution of asynchronous iterative algorithms on distributed environments has been proposed, constructs for asynchrony, impact on performance, and interactions with the API have not been well investigated. In this paper, we demonstrate the use of asynchronous algorithms in a distributed environment, prone to faults. With intuitive changes to the programming model of MapReduce, we show that data locality along with asynchrony can be safely exploited. Furthermore, the cost of synchronization (due to heavy network overheads) is significantly higher in a distributed setting compared to tightly-coupled parallel computers, leading to higher gains in performance and scalability.

Over the past few years, the MapReduce programming model has gained attention primarily because of its simple programming model and the wide range of underlying hardware environments. There have been efforts exploring both the systems aspects as well as the application base for MapReduce. A number of efforts [6, 11, 14] target optimizations to the MapReduce runtime and scheduling systems. Proposals include dynamic resource allocation to fit job requirements and system capabilities to detect and eliminate bottlenecks within a job. Such improvements combined with our efficient application semantics, would significantly increase the scope and scalability of MapReduce applications. The simplicity of MapReduce programming model has also motivated its use in traditional shared memory systems [10].

A significant part of a typical Hadoop execution corresponds to the underlying communication and I/O. This happens even though the MapReduce runtime attempts to reduce communication by trying to instantiate a task at the node or the rack where the data is present. Afrati et al.⁶ study this important problem and propose alternate computational models for sorting applications to reduce communication between hosts in different racks. Our extended semantics deal with the same problem but, from an application’s perspective, independent of the underlying hardware resources.

Recently, various forms of partial aggregations, similar to combiners in the MapReduce paper [4], have been shown to significantly reduce network overheads during global synchronization [13]. These efforts focus on different mathematical properties of aggregators (commutative and associative), which can be leveraged by the runtime to dynamically setup a pipelined tree-structured partial aggregation. These efforts do not address the problem of reducing the number of global synchronizations. In contrast, we focus on the algorithmic properties of the application to reduce the number of global synchronizations and its associated

⁶Foto N. Afrati and Jeffrey D. Ullman: A New Computation Model for Rack-based Computing. http://infolab.stanford.edu/Ollman/pub/mapred.pdf network overheads. By combining optimizations such as tree-structured partial aggregation, with capabilities of the proposed local reduce operations, we can reduce network overhead further.

VIII. FUTURE WORK

The myriad tradeoffs associated with diverse overheads on different platforms pose intriguing challenges. We identify some of these challenges as they relate to our proposed solutions:

Generality of semantic extensions. We have demonstrated the use of partial synchronization and eager scheduling in the context of few applications. While we have argued in favor of their broader applicability, these claims must be quantitatively established. Currently, partial synchronization is restricted to a map and the granularity is determined by the input to the map. Taking the configuration of the system into account, one may support a hierarchy of synchronizations. Furthermore, several task-parallel applications with complex interactions are not naturally suited to traditional MapReduce formulations. Do the proposed set of semantic extensions apply to such applications as well?

Optimal granularity for maps. As shown in our work, as well as the results of others, the performance of a MapReduce program is a sensitive function of map granularity. An automated technique, based on execution traces and sampling [5] can potentially deliver these performance increments without burdening the programmer with locality enhancing aggregations.

System-level enhancements. Often times, when executing iterative MapReduce programs, the output of one iteration is needed in the next iteration. Currently, the output from a reduction is written to the (distributed) file system (DFS) and must be accessed from the DFS by the next set of maps. This involves significant overhead. Using online data structures (for example, Bigtable) provides credible alternatives; however, issues of fault tolerance must be resolved.

IX. Conclusion

In this paper, we motivate MapReduce as a platform for distributed execution of asynchronous algorithms. We propose partial synchronization techniques to alleviate global synchronization overheads. We demonstrate that when combined with locality enhancing techniques and algorithmic asynchrony, these extensions are capable of yielding significant performance improvements. We demonstrate our results in the context of the problem of computing PageRanks on a web graph, find the Shortest Path to any node from a source, and K-Means clustering on US census data. Our results strongly motivate the use of partial synchronizations for broad application classes. Finally, these enhancements in performance do not adversely impact the programmability and fault-tolerance features of the underlying MapReduce framework.

Acknowledgments

The authors would like to acknowledge Mr. Ashish

Gandhe for discussions and for his input on coding various applications. This work was supported in part by the

National Science Foundation under grant IIS-0844500.

References

[1]    J.M. Bahi. Asynchronous iterative algorithms for non-expansive linear system. J. Parallel Distrib. Comput., 60(1), 2000.

[2]    C.-T Chu, S.K. Kim, Y.-A. Lin, Y. Yu, G. Bradski, A.Y. Ng, and K. Olukotun. Map-reduce for machine learning on multicore. Advances in Neural Information Processing Systems 19, 2007.

[3]    Price D. J. de S. A general theory of bibliometric and other cumulative advantage processes. J. of the American Society for Information Science, Vol 27, 292306, 1976.

[4]    J. Dean and S. Ghemawat. Mapreduce: Simplified data processing on large clusters. USENIX OSDI, 2004.

[5]    R.O. Duda, P.E. Hart, and D.G. Stork. Chapter 8. pattern classication. A Wiley-Interscience Publication, 2001.

[6]    K. Kambatla, A. Pathak, and H. Pucha. Towards optimizing hadoop provisioning for the cloud. USENIX HotCloud, 2009.

[7]    K. Kambatla, N. Rapolu, S. Jagannathan, and A. Grama. Relaxed synchronization and eager scheduling in mapreduce. Purdue University Technical Report CSD TR #09-010, 2009.

[8]    L. Liu and Z. Li. Improving parallelism and locality with asynchronous algorithms. ACM PPoPP, 2010.

[9]    J.C. Miellou, D. El Baz, and P. Spiteri. A new class of asynchronous iterative algorithms with order intervals. Math. Comput., 67(221), 1998.

[10]    C. Ranger, R. Raghuraman, A. Penmetsa, G. Bradski, and C. Kozyrakis. Evaluating mapreduce for multi-core and multiprocessor system. IEEE HPCA, 2007.

[11]    T. Sandholm and K. Lai. Mapreduce optimization using dynamic regulated prioritization. ACM SIGMETRIC-S/Performance ’09, 2009.

[12]    E. Yom-tov and N. Slonim. Parallel pairwise clustering. SDM, 2009.

[13]    Y. Yu, P.K. Gunda, and M. Isard. Distributed aggregation for data-parallel computing: interfaces and implementations. ACM SOSP, 2009.

[14]    M. Zaharia, A. Konwinski, A. Joseph, R. Katz, and I. Stoica. Improving mapreduce performance in heterogeneous environments. USENIX OSDI, 2008.

1

2

METIS. http://glaros.dtc.umn.edu/gkhome/views/metis/

3

Apache Mahout. http://lucene.apache.org/mahout/

4

US Census Data, 1990. UCI Machine Learning Repository: http://kdd.ics.uci.edu/databases/census1990/USCensus1990.html