Нечёткая модель и алгоритм решения задачи выбора медикаментозной терапии

Аннотация

Селякова С.М. Нечеткая модель и алгоритм решения задачи выбора медикаментозной терапии. В статья приведена постановка многокритериальной нечёткой задачи принятия решений при выборе медикаментозной терапии, в частности, при лечении бронхообструктивного синдрома у детей. Рассмотрен алгоритм её решения, основанный на методах сведения нечётких задач к чётким через введение множеств уровня α.

Актуальность

В процессе установления диагноза и выработки рекомендуемого лечения врач сталкивается с целой последовательностью сложных решений, которые в большинстве случаев находятся эвристическим путём исходя из его опыта и интуиции. В первую очередь практическая деятельность врача начинается с установления диагноза в результате итерационного процесса, каждый этап которого состоит из логического анализа и дополнительных исследований, сужающих шаг за шагом круг возможных диагнозов. Безусловно, основная цель установления диагноза – назначение соответствующего лечения. При этом, как правило, существует несколько возможных методов лечения, и выбор одного из них может происходить в различных условиях: в условиях определённости (в бесспорной ситуации), в условиях риска и в условиях неопределённости. В подобных задачах принятия решений присутствует также неопределённость, связанная с расплывчатым, нечётким описанием критериев принятия решений и параметров объекта (процесса диагностики и лечения), наличием критериев, не измеряемых в количественных шкалах. Кроме того, для оценки объекта по критериям, измеряемым в шкале интервалов или порядка, используется экспертная информация в форме балльных или словесных градаций.

Таким образом, расплывчатый характер описаний в постановке задач принятия врачебных решений и в предпочтениях экспертов при выборе метода лечения приводит к необходимости применения методов теории нечётких множеств и нечёткого математического программирования.

Анализ литературных источников.

Информация, на основании которой лицу, принимающему решения (ЛПР), например врачу, приходится принимать решения, является неоднородной в силу гетерогенности как самого объекта, так и внешнего окружения. Вследствие этого наиболее распространёнными методами, применяемыми в медицинской диагностике и при выборе решений в процессе лечения пациента, являются методы математической логики, теории вероятности и теории игр [1, 2]. Вместе с тем, в последнее время значительное распространение в медицине получили методы теории нечётких множеств, нечёткой логики и искусственных нейронных сетей [3, 4].

Как показывают исследования отечественных и зарубежных ученых, значительного повышения эффективности лечебно-оздоровительных процедур при лечении различных заболеваний можно ожидать за счёт использования различных методов терапии, находящихся под управлением современных информационных технологий, в частности, экспертных систем и систем поддержки принятия решений [5, 6]. Применение приведённых методов и подходов на практике позволяет значительно повысить скорость принимаемых решений в условиях ограниченности, субъективности, размытости и неточности информации.

Цель статьи.

Сформулировать физическую постановку многокритериальной нечёткой задачи принятия решений при выборе медикаментозной терапии для пациента с учётом различной формы тяжести протекания заболевания и привести алгоритм её решения.

Постановка задачи принятия решений.

Пусть имеются математические модели прогноза изменения состояния пациента в результате применения медикаментозной терапии, которые с требуемой точностью описывают влияние назначаемого набора дозировок лекарственных препаратов u=(u₁,...,u_n) (вектора управляющих параметров), на вектор выходных параметров z=(z₁,...,u_n), который характеризует эффективность назначенного лечения с учётом различной степени тяжести протекания заболевания:  

 z_i=f_i(u₁,...,u_n;α_i), i=1,...,m,                                                                    (1)

где α_i – нечёткие параметры, характеризующие степень тяжести заболевания.

Ограничения, наложенные на составляющие векторов u и z, которые определяют их допустимые области измерения, представим в следующем виде:

g_j(u,z)≥0, j=1,...,J.                                                                      (2)     

Частные целевые функции f_i(u₁,...,u_n;α_i), i=1,...,m составляют векторную функцию f и различаются своими коэффициентами относительной важности (весами) (γ₁,...,γ_m), значения которых могут изменяться.

Требуется найти вектор управления  u*=(u^*₁,...,u^*_n), обеспечивающий наилучшее приближение к желаемым значениям локальных критериев  f^*_i:

                                     

где f_i(u,α_i) – нечёткие локальные критерии, значения которых вычисляются по моделям;  f^*_i – желательные (идеальные) значения локальных критериев, задаваемых ЛПР; g_j(u) – ограничения на составляющие вектора u; b_j – заданные числа;  – множество уровня α нечётких параметров 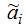, введённое для учёта нечёткости параметров α_i.

Для примера рассмотрим процесс лечения бронхообструктивного синдрома у детей с острыми респираторными заболеваниями. Развитие транзиторного состояния бронхиальной обструкции возникает в раннем возрасте и обусловлено анатомо-физиологическими особенностями ребёнка на фоне вирусных инфекций и исчезает к 6 годам, а также не ведет к формированию какой-либо нозологической формы в более позднем возрасте. Однако рецидивирующий (повторяющийся) обструктивный синдром является главным фактором риска снижения легочной функции. Повторные эпизоды респираторных заболеваний, сопровождающихся бронхиальной обструкцией, как правило, усугубляют бронхиальную гиперреактивность и создают условия для реализации генерализованной реакции и повышенной чувствительности с формированием хронических форм бронхитов или бронхиальной астмы.

В качестве вектора управляющих параметров u= (u₁,...,u_n) выступает набор дозировок n препаратов назначаемой базисной и ингаляционной терапии. В качестве базисной терапии, как правило, назначаются противовирусные препараты (интерферон, свечи с вифероном, ремантадин, арбидол, гропринозин), отхаркивающие и муколитические средства, β₂-агонисты короткого действия, антихолинергические  препараты, теофиллины  короткого  действия  и  их  сочетание,  антигистаминные препараты I и II поколения, противовоспалительные средства. Ингаляционная терапия проводится при помощи небулайзера такими препаратами как «Беродуал», «Ипратропия бромид», «Пульмикорт» и т.п.

Нечёткие параметры α_i зададим в виде лингвистической переменной, которая будет характеризовать тяжесть бронхиальной обструкции. Допустим, лингвистическая  переменная α_i будет состоять из трёх термов, что будут характеризовать лёгкую, среднюю и тяжёлую форму протекания заболевания.

Эффективность лечения бронхообструктивного синдрома у детей, как правило, оценивается по следующим критериям [7]: выраженность основных симптомов бронхиальной обструкции (f₁), улучшение состояния пациента при анализе катамнеза (f₂), иммуномодулирующий эффект проводимой терапии (f₃), которые составляют векторную функцию f и различаются весами. Иммуномодулирующий эффект проводимой терапии оценивается по основным показателям иммунограммы, к которым относятся: количество лейкоцитов, палочкоядерных, сегментоядерных, %; эозинофилов, %; лимфоцитов, %; моноцитов; фагоцитарный индекс, %; фагоцитарное число, %; ЦИК; CD3 (Т-лимфоциты), %; CD4 (Т-хелперы), %; CD8 (Т-супрессоры киллеры), %; CD4/CD8 (иммунорегуляторный индекс); CD20 (В-лимфоциты), %; CD16 (NK-клетки), %; IgA общий, г/л; IgM общий, г/л; IgG общий, г/л.

Решение задачи исследования.

Для решения подобных задач целесообразно использовать подход, основанный на принципе гарантированного результата [8]. В этом случае производится минимизация наибольшего отклонения нечётких значений локальных критериев от их эталонных значений при выполнении наложенных ограничений:

                                          

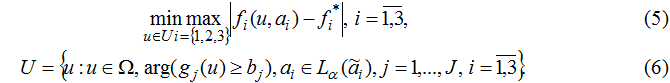
При нечётких ограничениях в задаче (5)-(6) необходимо построить функцию принадлежности μ_j(u), j=1,J выполнения каждого из ограничений g _j≥b_j, j=1,J.

Целесообразность минимаксной постановки задачи принятия решений можно объяснить тем, что назначенная терапия должна обеспечивать гарантированный результат выздоровления пациента.

Данную задачу многокритериальной оптимизации в условиях неопределённости можно свести к задаче многокритериальной оптимизации на основе множеств уровня α, что позволит осуществить поиск рациональных вариантов решения по выбираемым критериям [8].

Предлагается использовать следующий алгоритм решения задачи:

1. Выделить диапазоны значений α для различных степеней тяжести протекания заболевания. Например, могут быть выделены следующие степени тяжести (СТ) заболевания:

СТ=1, при  0,7≤α≤1,0 - тяжёлая форма;

СТ=2, при 0,3≤α≤0,7 - средняя форма;

СТ=3, при 0,0≤α≤0,3 - лёгкая форма.

2. ЛПР должен назначить желательные (эталонные) значения локальных критериев  f^*_i.

3. Рассчитать минимаксные (гарантированные) варианты решения задачи (5)-(6) при различных формах тяжести бронхиальной обструкции.

4. ЛПР должен выбрать из полученного множества решений задачи наиболее приемлемый вариант с учётом имеющейся степени тяжести протекания заболевания. Если вариант не выбран, то ЛПР должен скорректировать f^*_i (вернуться к пункту 2) и заново рассчитать минимаксные варианты решения задачи.

5. Поиск прекратить. Вывести значения  f^*_i(u,α_i), СТ и рекомендуемый вектор управления – u*=(u^*₁,...,u^*_n).

Итерационная процедура последовательной минимизации максимального отклонения значений локальных критериев от эталонов повторяется до тех пор, пока ЛПР не удовлетворят текущие результаты.

Предложенный алгоритм решения задачи, основанный на сочетании методов идеальной точки и гарантированного результата, позволяет эффективно решать такие задачи принятия решений, в которых значения локальных критериев характеризуются размытостью.

Выводы.

Применение предложенной нечёткой модели в задаче выбора медикаментозной терапии позволит повысить эффективность лечебно-оздоровительных процедур при лечении различных заболеваний с учётом различной степени тяжести протекания заболевания.

Дальнейшее развитие полученных результатов в задаче принятия решений при выборе терапии может быть связано с учётом в разработанной модели возраста пациентов и наличия сопутствующих заболеваний.

Литература

1. Руанет В.В. Информационные технологии в медицине – введение в медицинскую информатику / В.В. Руанет, А.К. Хетагурова. – М.: МАКСПресс, 2003. – 67 с.
2. Беллман Р. Математические методы в медицине: [пер. с англ.] / Р. Беллманn под ред. Л.Н. Белых. – М.: Мир, 1987. – 200 с.
3. Борисов А.Н. Принятие решений на основе нечётких моделей. Примеры использования / А.Н. Борисов, О.А. Крумберг, И.П. Фёдоров. – Рига: Зинатне, 1990. – 184 с.
4. Кореневский Н.А. Проектирование систем принятия решений на нечетких сетевых моделях в задачах медицинской диагностики и прогнозирования / Н.А. Кореневский // Вестник новых медицинских технологий. – 2006. – Т. XIII, №2. – С. 6–9.
5. Чернов В.И. Медицинская информатика / В.И. Чернов, И.Э. Есауленко, И.Г. Сидорович. - М.: Феникс, 2007. –  320с.
6. Кореневский Н.А. Проектирование систем поддержки принятия решений для медико-экологических приложений / Н.А. Кореневский и др. – Курск: КГТУ, 2004.– 180 с.
7. Гамиева Е.В. Новые технологии в лечении бронхообструктивного синдрома у детей с острыми респираторными заболеваниями / Е.В. Гамиева, В.В. Лазарев // Вестник новых медицинских технологий. – 2009. – Т. XVI, №3. – С. 190–191.
   
8. Рыков А.С. Модели и методы системного анализа: принятие решений и оптимизация: [учебное пособие для вузов] / А.С. Рыков. – М.: «МИСИС», Издательский дом «Руда и металлы», 2005. – 352 с.