Динамика модели задержки инфекции вируса гепатита В с ростом гепатоцита

Аннотация

Айкенберри Ш., Хюс С., Нэджи Д.Д., Куан Я. Динамика модели задержки инфекции вируса гепатита В с ростом гепатоцита. Хроническим вирусом гепатита B страдает около 350 миллионов человек и это может является причиной их смерти. В статье проведен анализ динамических моделей, рассмотрен логистический рост гепатоцита. Модель (приведенная в статье) также рассматривает явную временную задержку в вирусном возпроизводстве. С такой формулировкой все образцовые параметры могут быть оценены с помощью биологических данных. Также производиться моделирование обнаружения вируса и моделирование соответствующего курса ламивудиновой терапии, Именно это позволяет модели давать хорошее результаты. Предыдущие модели, рассматривали постоянный рост гепатоцита и это давало только две динамические возможности: сходимость к свободному вирусу или хроническое устойчивое состояние. Наша модель допускает третью возможность – длительные колебания. Когда основное репродуктивное число больше, чем 1, то существует биологически значимое хроническое устойчивое состояние, и стабильность этого устойчивого состояния зависит и от темпа регенерации гепатоцита и от ядовитости болезни. Поэтому, часто внезапное начало печеночной недостаточности у хронических пациентов вируса гепатита B может быть объяснено как выключатель стабильности, вызванной постепенным развитием параметров, представляющих болезненное состояние.

Вступление

Вирус гепатита В (ВГВ) вызывает огромное количество человеческих смертей, особенно в Азии, к югу от Сахары, части Аравийского полуострова, южной части Тихого океана, тропической Южной Америке и арктической Северной Америке [1]. В настоящее время около двух миллиардов человек (примерно 30 % от общего количества людей) заражались гепатитом. Вирус нацелен на печень, и 17,5 %  из тех, кто имеет активную инфекцию вируса гепатита B страдает на хронический гепатит [34]. До 0.06 % зараженных вирусом гепатита B людей умрет от осложнений, связанных с болезнью в течение 21 года. Но смертность не единственный способ, которым вирус гепатита B влияет на народонаселение. В период времени от недели до месяца инфицированные имели симптомы: тошнота, усталость, желтуха и боли в суставах, а иногда и цирроз печени.

В первую очередь из-за значимости ВГВ, как глобально опасного для здоровья населения, вируса и связанными с ним болезни все это привело к необходимости использовать математическую и теоретическую биологии [10, 27, 29, 30, 7, 6]. Модели, как правило, используются для изучения динамики ВГВ внутри хозяина. Модель, сосредоточена как на здоровые клетки, так и инфицированные. Большинство из этих моделей показывают вирусную инфекцию как процесс действующих масс между зараженных и здоровых клеток. Например, следующий феноменологическая модель широко используется при изучении ВГВ и других вирусных заболеваний, в том числе и ВИЧ:

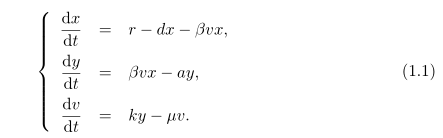
Число или масса здоровых клеток – x, число инфицированных клеток – y и v – количество вируса в организме. Здоровые гепатоциты входят в печень из внешнего источника по уровню r, и гепатоциты умирают по уровню d.

Термин "массовая акция" используются для моделирования инфекции здоровых гепатоцитов по нескольким направлениям. Гурли и соавт. [10] показал, что это предположение составляет основное репродуктивное число R0, которое зависет от гомеостатического размера печени r/d. Таким образом эта модель делает сомнительное предсказание, что люди с меньшей печенью должны быть менее восприимчивы к инфекции вируса гепатита B. Кроме того, у постоянной массовой акции β, нет четкого биологического значения. Гурли и соавт. [10] в расширенной модели (1.1), инфекцию вируса гепатита B здоровых клеток представляли  не как "массовая акция", а стандартной функцией уровня. В частности термин массовой акции в (1.1) заменен на:

где T – общее количество клеток печени, зараженных или нет. Под их формулировкой R0 теряет свою зависимость от размера печени. Кроме того, β в (1.2) имеет четкое биологическое значение. Это может интерпретироваться или как максимальный уровень, по которому вирус заражает здоровые клетки, или как вероятность, что единственный вирус заражает любую клетку в здоровой печени в интервале единицы времени.

Недостаток модели (1.1) и Гурли и соавт. в формулировки – предположение, что здоровые гепатоциты пополняются по постоянному уровню. Математически, это предположение ограничивает позволенное асимптотическое поведение только двумя универсальными случаями [10, 27, 29, 30]: если R0> 1, тогда к постоянному хроническому устойчивому состоянию приближаются во всех случаях.

Предположение о постоянном гепатоцитном притоке на биологических основаниях имеет несоответствие. Установлено, что регенерация печени после раны достигается путем быстрого увеличения гепатоцита [26, 19, 31]. Кроме того, как мы утверждали выше, регенерацию печени заканчивается после частичного удаления ее. В моделях животных, подразумевает, что значительное увеличение гепатоцита зависит от массы печени. Поэтому, мы предлагаем альтернативную модель динамики вируса гепатита B, в которой темп быстрого увеличения гепатоцита описан логистической функцией. Мы показываем, что это предположение может быть верным и при R0> 1. В частности асимптотическое поведение может возникнуть от стабильного хронического равновесия до привлекающей периодической нестабильности хронического равновесия. На это влияет и ядовитостью инфекции, и ее уровень, по которому гепатоциты восстанавливаются. Мы утверждаем, что постепенное развитие параметров, описывающих регенерацию печени и ядовитость вируса гепатита B в течение хронической инфекции, может привести к внезапному изменению в динамике болезни, поскольку "выключатель" стабильности нарушен. Модель предсказывает, что начало острой печеночной недостаточности может быть смоделировано.

Преимущество этой модели состоит еще и в том, что все параметры могут быть оценены непосредственно с помощью эмпирических биологических данных. Чтобы утвердить наш подход, мы моделируем нахождение вируса и курс терапия.

Полная модель

Печень обладает замечательной способностью к регенерации после травмы. Эту регенерацию стимулируют нормальные гепатоциты, которые в отличие от неизлечимо дифференцированных клеток, доминируют над большинством других тканей. Кроме того, эта регенерация происходит по чрезвычайно быстрому уровню. Например, печень крысы полностью восстанавливает в течение недели после экспериментального удаления двух третей печени [26]. Регенерация достигнута несколькими циклами митоза с помощью вовлечения большой части зрелых гепатоцитов, хотя меньше количество гепатоцитов участвует в каждом последующем цикле [26, 31]. Объектом дискуссии является то как эти регенеративные циклы начинаются и чем управляют. Но экспериментальное удаление печени, кажется, играет важную роль. Удаление 2/3 печени приводит к тому, что увеличивается объем протекания крови через вены [25].

Тем не менее, регенеративное распространение происходит только тогда, когда фактическая масса печени уменьшается. После удаления части печени, регенеративный ответ может увеличить после дополнительного резекции, по крайней мере, спустя 10 часов. Кроме того, регенерации может уменьшаться в ответ на трансплантата печени (увеличение массы печени) до 18 часов после первоначального резекции. Эти результаты убедительно свидетельствуют о том, что гепатоцитов пролиферативная активность контролируется фактической массы печени и, что гемодинамика играть роль в подготовке гепатоциты для пролиферации. Таким образом, можно сделать вывод, что сигнал роста гепатоцитов прямо пропорционален общей популяции клеток печени, и что уровень сигнала приблизительно равномерен по всей печени.

Как Гурли и др. [10] мы используем стандартную функцию уровня, чтобы позволяет описать вирусную инфекцию здоровых клеток и явно рассмотреть задержку между вирусной инфекцией и производством. Эти соображениям соответствует следующую модель:

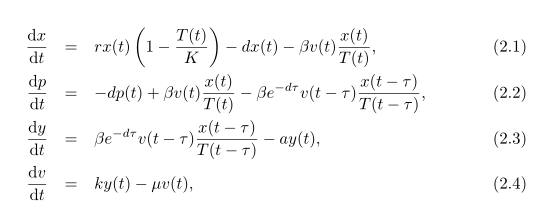
где

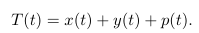
Упростим анализ:

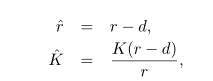
и перепишем уравнение (2.1) как

Число здоровых гепатоцитов – x(t), p(t) – число здоровых клеток, которые были заражены, но еще не производят вирус (скрытая инфекция), y (t) – число инфицированных клеток, активно производящих вирусов (продуктивно инфицированные клетки), и v (t) является числом свободного вируса.

Список использованной литературы

1.P.M. Arguin, P.E. Kozarsky and C. Reed [eds], “CDC Health Information for International Travel 2008,” Elsevier, Philadelphia, 2007.

2.E. Beretta and Y. Kuang, Geometric stability switch criteria in delay dsfferential systems with delay dependent parameters, SIAM J. Math. Anal., 33 (2002), 1144–1165.

3.F. Berezovsky, G. Karev, B. Song and C. Castillo-Chavez, A simple epidemic model with surprising dynamics, Math. Biosci. Eng., 1 (2004), 1–20.

4.M. Bralet, S. Branchereau, C. Brechot and N. Ferry, Cell lineage study in the liver using retroviral mediated gene transfer, Am. J. Pathol., 144 (1994), 896–905.

5.C. Castillo-Chavez, K. Cooke, W. Huang and S. A. Levin, On the role of long incubation periods in the dynamics of acquired immunodeficiency syndrome (AIDS), J. Math. Biol., 27 (1989), 373–398.

6.S.M. Ciupe, R.M. Ribeiro, P.W. Nelson, G. Dusheiko and A.S. Perelson, The role of cells refractory to productive infection in acute hepatitis B viral dynamics, Proc. Natl. Acad. Sci. USA, 104 (2007), 5050-5055.

7.S.M. Ciupe, R.M. Ribeiro, P.W. Nelson and A.S. Perelson, Modeling the mechanisms of acute hepatitis B virus infection, J. Theor. Biol., 247 (2007), 23–35.

8.G. Ferir, S. Kaptein, J. Neyts and E. De Clercq, Antiviral treatment of chronic hepatisis B virus infections: The past, present and the future, Rev. Med. Virol., 18 (2008), 19–34.

9.S.A. Gourley and Y. Kuang, A stage structured predator-prey model and its dependence on maturation delay and death rate, J. Math. Biol., 49 (2004), 188–200.

10.S.A. Gourley, Y. Kuang and J.D. Nagy, Dynamics of a delay differential equation model of hepatitis B virus infection, J. Biological Dynamics, 2 (2008), 140–153.

11.C.D. Gove and R.D. Hughes, Liver regeneration in relationship to acute liver failure, Gut, (Suppl.), 32 (1991), S92–S96.

12.L.G. Guidotti and F.V. Chisari, Immunobiology and pathogenesis of viral hepatitis, Annu. Rev. Pathol. Mech. Dis., 1 (2006), 23–61.

13.S.B. Hsu, T.W. Hwang and Y. Kuang, Global analysis of the Michaelis-Menten type ratio-dependent predator-prey system, J. Math. Biol., 42 (2001), 489–506.

14.T.W. Hwang and Y. Kuang, Deterministic extinction effect of parasites on host populations, J. Math. Biol., 46 (2003), 17–30.

15.T.W. Hwang and Y. Kuang, Host extinction dynamics in a simple parasite-host interaction model, Math. Biosci. Eng., 2 (2005), 743-751.

16.M. Iannacone, G. Sitia, Z.M. Ruggeri and L.G. Guiddotti, HBV pathogenesis in animal models: recent advances on the role of platelets, J. Hepatol., 46 (2007), 719–726.

17.Y. Kuang, “Delay Differential Equations with Applications in Population Dynamics,” Math-ematics in Science and Engineering 191, Academic Press, Boston, 1993.

18.Y. Kuang and E. Beretta, Global qualitative analysis of a ratio-dependent predator-prey sys-tem, J. Math. Biol., 36 (1998), 389–406.

19.L. Lambotte, A. Saliez, S. Triest, E.M. Tagliaferri, A.P. Barker and B.G. Andrzej, Control of rate and extent of the proliferative response after partial hepatectomy, Am. J. Physiol. Gastrointest. Liver Physiol., 273 (1997), G905–G912.

20.G.K.K. Lau, T. Piratvisuth, K.X. Luo, P. Marcellin, S. Thongsawat and G. Cooksley et al., Peginterferon Alfa-2a, lamivudine, and the combination for HBeAg-positive chronic hepatitis B, New Eng. J. Med., 352 (2005), 2682–2695.

21.D. Lavanchy, Worldwide epidemiology of HBV infection, disease burden, and vaccine preven-tion, J. Clin. Virol., 34 (2005), S1–S3.

22.W.M. Lee, Acute liver failure, N. Engl. J. Med., 329 (1993), 1862–1872.

23.M. Liu, C.W.Y. Chan, I. McGilvray, Q. Ning and G.A. Levy, Fulminant viral hepatitis: molecular and cellular basis, and clinical implications, Expert Rev. Mol. Med., 3 (2001), 1–19.

24.R.A. MacDonald, “Lifespan” of liver cells. Autoradio-graphic study using tritiated thymidine in normal, cirrhotic, and partially hepatectomized rats, Arch. Intern. Med., 107 (1961), 335– 343.

25.S. Marubashi, M. Sakon, H. Nagano, K. Gotoh, K. Hashimoto, M. Kubota, S. Kobayashi, S. Yamamoto, A. Miyamoto, K. Dono, S. Nakamori, K. Umeshita and M. Monden, Eect of portal hemodynamics on liver regeneration studied in a novel portohepatic shunt rat model, Surgery, 136 (2004), 1028–1037.

26.G. K. Michalopoulos, Liver regeneration, J. Cell. Physiol., 213 (2007), 286-300.

27.L. Min, Y. Su and Y. Kuang, Mathematical analysis of a basic virus infection model with application to HBV infection, Rocky Mountain Journal of Mathematics, 38 (2008), 1–13.

28.J.M. Murray, R.H. Purcell, S.F. Wieland, The half-life of hepatitis B virions, Hepatology, 44 (2006), 1117–1121.

29.M.A. Nowak, S. Bonhoeffer, A.M. Hill, R. Boehme, H.C. Thomas and H. McDade, Viral dynamics in hepatitis B virus infection, Proc. Natl. Acad. Sci. USA, 93 (1996), 4398–4402.

30.M.A. Nowak and R. M. May, “Virus Dynamics,” Oxford University Press, Oxford, 2000.

31.J. Rozga, Hepatocyte proliferation in health and in liver failure, Med. Sci. Monit., 8 (2002),RA32–38.

32.S.A. Whalley, J.M. Murray, D. Brown, G.J.M. Webster, V.C. Emery, G.M. Dusheiko and A.S. Perelson, Kinetics of acute hepatitis B virus infection in humans, J. Exp. Med., 193 (2001), 847-853.

33.H.K. Wolf and G.K. Michalopoulos, Hepatocyte regeneration in acute fulminant and non-fulminant hepatitis: A study of proliferating cell nuclear antigen expression, Hepatology, 15 (1992), 707–713.

34.World Health Organization, 2000, Hepatitis B fact sheet No. 204, WHO Website.

35.B. Wu, C. Li, H. Chen, J. Chang, K. Jeng, C. Chou, M. Hsu and T. Tsai, Blocking of G1/S transition and cell death in the regenerating liver of hepatitis B virus X protein transgenic mice, Biochem. Biophys. Res. Commun., 340 (2006), 916–928.

36.H. Zou and X. Zou, Impact of delays in cell infection and virus production on HIV-1 dynamics, Math. Med. Biol., 25 (2008), 99–112.