Сложность геометрического образа
В мире актуальным является исследование сложности дискретных структур. В работе предлагается считать показатель сложности линейной формулой по критерию общедоступному для понимания. Остальные исследователи используют процедурный подход Ќжадныхќ алгоритмов, и выбранный критерий сложности не всегда справедлив в теории компьютерного зрения. В качестве входных данных компьютерного эксперимента расчета показателя сложности использованы зрительные образы алфавитно-цифровой последовательности (АЦП) арабских цифр, некоторых графических символов и прописных букв русского алфавита. Полученные результаты сложности АЦП использованы для дальнейшего кластерного анализа алфавита русского языка по выявлению системных признаков распознавания графических образов букв.
Черно-белый растровый зрительный образ является однородной дискретной структурой двухмерного поля бинарных чисел. В работе Арнольда В.И. [1] изучается сложность последовательности нулей и единиц. Последовательность является одномерной дискретной структурой, а растровое изображение двухмерное. Вектор последовательности нулей и единиц можно единообразно представить двухмерным образом квадратной формы, если количество элементов вектора кратно некоторому основанию N в квадрате. Для расчета сложности необходимо построить топологический граф и определить длину пути до анализируемой компоненты. Процедуры построения графа и поиска пути итерационные и рекуррентные, что требует значительных вычислительных затрат. Предложенный Арнольдом В.И. процедурный подход к расчету сложности не применим в анализе большого количества зрительных образов или вычислении в реальном времени сложности образа большого разрешения.
Показатель сложности впервые использован Эдвином Олсоном для синтеза лексикографического кода расширенной реальности [2]. Метод построения кода AprilTag включает проверку на геометрическую сложность генерируемого маркера. Используется Ќжадныйќ алгоритм для двухмерного растрового образа размером 6 на 6 ячеек. Аппроксимация образа осуществляется итерационным подбором прямоугольной области с максимальным значением одного из бинарных цветов и с минимальным значением вкрапления ячеек другого цвета. Ячейки найденной прямоугольной области базового цвета помечаются Ќкак использованныеќ и не участвуют в дальнейшем анализе. Прямоугольная область может содержать помеченные ячейки, но они не участвуют в анализе. Работа Ќжадногоќ алгоритма заканчивается, когда помечены все ячейки. Если на холсте последовательно рисовать, наложив друг на друга все найденные прямоугольные области выбранного цвета, то получится цифровой коллаж, точно отражающий исходный зрительный образ. Показателем сложности по Олсону Э. будет количество найденных прямоугольных областей. Аффинное вращение на прямой угол образа кода является естественным в восприятии его человеком Ќтем же самымќ, но перевернутым в зависимости от контекста {влево, вправо, вверх, вниз}. Предложенный алгоритм Олсоном Э. может посчитать разное значение сложности четырёх аффинных подобразов, что не приемлемо как критерий сложности для систем технического зрения.
В теории формальных систем, если построены все последовательности рекуррентных форм слов, то можно использовать числовой показатель сложности, предложенный Твердохлебовым В.А. в работе [стр. 35, 3]. Показательная формула является отношением числа знаков в последовательности, порожденных применением рекуррентной формы символьной структуры, к мощности алфавита. Применение в таком виде формулы требует процедурного порождения рекуррентных форм, но не требует поиска пути как в ресурсоёмком подходе Арнольда В.И. По утверждению Твердохлебова В.А., обобщенная формула числового показателя является грубой оценкой сложности.
Пример грубой оценки показателя сложности, как отношения длины к мощности, использован в работе [4] для оценки сложности клеточных структур. В работе предложена формула: периметр геометрической фигуры возводится в квадрат и делится на её площадь. В однородной дискретной структуре квадратных ячеек фиксированного размера r двухмерной ограниченной области достаточно посчитать количество сторон ячеек цвета объекта K, соприкасающихся в 4-х связной окрестности фон Неймана с ячейками цвета фона. Причем всегда подразумевается, что ячейки на границе области виртуально соприкасаются с ячейками цвета фона. Популяция ячеек цвета объекта E – это их количество. Тогда получаем аналог формулы, предложенной в работе [4], только для черно-белого растрового изображения: (r•K)^2/(r•r•E). С точки зрения компьютерного дизайна и инженерной графики, критерий является грубым. На рисунке 1 показаны две фигуры 6х5 с разной сложностью, но одинаковой площадью и одинаковым периметром.
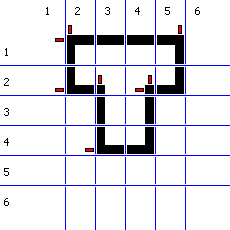
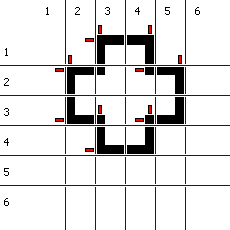
Рисунок 1 – Фигуры для сравнения грубой оценки сложности
В работе предлогается критерий вычисления сложности F, как количество прямых штрихов, которыми нарисован образ. Для вычисления сложности F используется линейная формула: сумма булевых функций детектирующих начало вертикального или горизонтального штриха. На рисунке 1 штрихи отмечены колышками. Для синтеза формулы сложности F используется логика предикатов второго порядка [5].
Компьютерный эксперимент. Используется растровое изображение символов АЦП, нарисованных шрифтом Arial размером 36 пунктов. Черно-белое представление символов имеет размер 36х36 точек, что в итоге дает бинарную последовательность из 1296 компонент. Вычислим сложность образа некоторых графических символов и их популяцию ячеек цвета объекта (F\E):
{0-88\110, ?-52\341, ?-8\164, Њ-4\506, #-72\431, *-64\109}
Для образов символов цифр имеет следующие результаты:
{ “0”-88\330, “1”-32\181, “2”-112\307, “3”-122\304, “4”-68\307, “5”-96\325, “6”-132\370, “7”-62\212, “8”-136\379, “9”-126\353 }После подсчета сложности образа прописных букв русского алфавита явно можно выделить распределение букв на 3 класса:
1-й класс: буквы сложностью от 6 до 46;2-й класс: буквы сложностью от 72 до 144;
3-й класс: буквы сложностью от 180 до 186.
Перечень букв попавших в соответствующий класс:
1-й класс: {Г,П,Т,Е,Н,Ц,Ш,Щ,Ё,Л,Д,Ч};2-й класс: {Р,Ь,Б,Ъ,Ы,В,М,И,К,А,Й,Ф,У,С,З,Э,О,Ю};
3-й класс: {Х,Ж}.
Выводы
Предложенный критерий оценки сложности F адекватен аффинным вращениям образа на прямой угол в системах технического зрения. Вычислительная формула сложности F приемлема для обработки образов большого разрешения. Буквы русского алфавита по геометрической сложности делятся на три непересекающихся кластера, что может быть использовано как системный признак в распознавании текстов.
Список использованных источников
1. Арнольд В.И. Сложность конечных последовательностей нулей и единиц и геометрия конечных функциональных пространств // Публичная лекция 13 мая 2006 г. [Электронный ресурс]. – Режим доступа: http://mms.math-net.ru/meetings/2005/arnold.pdf2. Edwin Olson. AprilTag: A robust and flexible visual fiducial system // In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), 9-13 May 2011, Shanghai, China, 2011. – P. 3400 – 3407.
3. Твердохлебов В. А. Геометрические образы законов функционирования автоматов. – Саратов: изд-во ЌНаучная книгаќ. – 2008. – 183 с.
4. Меркулова Е. В. Оценка функционального состояния клеток с использованием методов цифровой обработки изображений / Е. В. Меркулова, А. А. Трибрат, И. Г. Герасимов // Наук. праці Донецького нац. техніч. унів. Сер.: Обчислювальна техніка та автоматизація. –Донецьк: ДонНТУ. ? 2006. – Вип. 106. – С. 145 – 149.
5. Гудаев О.А. Синтез и анализ предложений графического языка передачи сообщений в мобильных робототехнических системах с элементами расширенной реальности (ARGET) // Искусственный интеллект. ? 2006. ? љ 2. ? С. 467 ? 498.