Аннотация
Ильенко Т.А. Моделирование процесса загрязнения атмосферы выбросами автомобильного транспорта.Выявлена необходимость в поиске новых подходов к моделированию загрязнения атмосферы выбросами автомобильного транспорта. Указаны основные элементы, участвующие в процессе распространения вредной примеси в атмосфере. Определена основная формула для построения модели в прикладном пакете MATLAB R2009b.
Постановка проблемы
В последние годы особенно актуальными стали проблемы, связанные с загрязнением атмосферы, так как человечество достигло пика в росте промышленного потенциала и развитии автотранспорта.
Автотранспорт является одним из основных показателей технико-экономического развития общества, он способствует удовлетворению социальных потребностей населения. Но, с другой стороны, он ежедневно оказывает негативное влияние, как на здоровье человека, так и на общее состояние окружающей среды. Выхлопы автотранспорта приводят к нарушению экологического равновесия. Ежедневно в воздушную среду попадает огромное количество смеси примерно из двухсот различных веществ. Большая часть двигателей автомобилей потребляет бензин, именно он при сгорании выделяет достаточно большое количество свинца, диоксида углерода, оксида углерода, оксида азота, углекислого газа. Таким образом, возникает необходимость в поиске нового подхода при построении моделей, описывающих процесс распространения вредных примесей в атмосфере. Для реализации этого необходимо решить следующие задачи:
- изучить существующую классификацию математических моделей, которые описывают распространение вредных примесей в атмосфере;
- провести анализ и выбрать класс математической модели, которая будет описывать распространение примеси в атмосфере;
- привести модель к виду, удобному для моделирования в прикладном пакете MATLAB R2009b.
Анализ литературы
В настоящее время значительное число работ посвящено исследованию загрязнения атмосферы промышленными и автомобильными выбросами. Подробная классификация и рассмотрение математических моделей приведены в монографии Бабкова В.С, Ткаченко Т.Ю. «Анализ математических моделей распространения примесей от точечных источников» [5]. Основные характеристики и особенности гауссовых моделей распространения вредных примесей в атмосфере приведены в монографии Семенчина Е.А, Кузякиной М.В. «Стохастические методы решения обратных задач в математической модели атмосферной диффузии» и Бызовой Н.Л., Гаргера Е.Г., Иванова В.Н., «Экспериментальные исследования атмосферной диффузии и расчеты рассеяния примесей» [4,5].
Цель статьи
Рассмотрение новых подходов к моделированию распространения вредных примесей в атмосфере, определение оптимальной математической модели для её построения в математических прикладных пакетах, для предоставления информации о состоянии загрязнения атмосферы экологическим службам и жителям города.
Проведем визуальное сравнение полученых схем. В целом схемы похожи, за исключением фрагмента, отвечающего за вычисление нового значения x.
Постановка задачи исследования
Рассмотрим задачу нахождения функции концентрации q(x,t,y,z), которая образуется при мгновенном выбросе в момент времени 
из точечного источника, размещенного в точке пространства с координатами 
. Интенсивность источника считается заданной величиной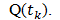 
. Линеаризованая модель распространения примеси имеет математическое решение при однородности проекций вектора скорости по пространственным координатам и задается уравнением параболического типа:
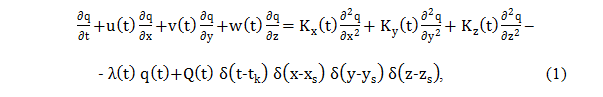
где Q - масса примеси, выделившейся при t=0 в начале координат;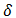 
- функция точечного источника; 
– составляющие коэффициента диффузии 
для соответствующих координатных осей; u, v, w – проекции скорости U (м / с) переноса примеси для соответствующих координатных осей; q – средняя концентрация примеси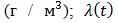 
; 
– скорость потери (стока) примеси (м / с).
Начальные условия выбираются по содержанию фундаментального решения 
=0, во всех точках кроме начала координат и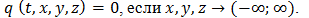 
.
В общем виде решение уравнения (1) выражает закономерности распространения примеси в неограниченном пространстве, когда коэффициенты диффузии (турбулентности)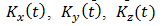 
и скорость стока считаются известными функциями времени, а скорость перемещения центра тяжести облака примеси, в направлении соответствующих осей, определяется составляющими вектора ветра 
.
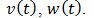Решение задач и результаты исследований
При моделировании процессов распространения примесей в трехмерной области предпочтение отдается аналитическому или численному решению полуэмпирического уравнения турбулентной диффузии в декартовых координатах [1,3].
Данная работа основывается на подходе, который был предложен в монографии Степаненко С.Н., Волошина В.Г., Типцова С.В. «Решение уравнения турбулентной диффузии для стационарного точечного источника» он заключается в новом решении полуэмпирического уравнения турбулентной диффузии [2]. Такое решение отличается от предыдущих тем, что учитывает взаимодействие составляющих скорости ветра и коэффициента диффузии и в направлении осей декартовой системы координат при условии, что молекулярный и турбулентный коэффициенты диффузии принимают определенные значения, а скорость ветра, в данном решении, больше либо равна нулю [2].
Если существует предел функции Q(t) при 
=, то уравнение будет описывать стационарное распределение примеси. Тогда для постоянно действующего источника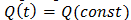 
нетрудно получить стационарную функцию в виде:
Особенностью формулы (2) является то, что если все составляющие скорости ветра равны нулю (штиль)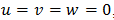 
, то уравнение (2) принимает вид:
где Q – мощность источника, (x, y, z) – декартовы координаты, K- сумма коэффициентов турбулентной и молекулярной диффузии [2].
Формула (3) позволяет найти только приближенное значение решения поставленной задачи. Но именно эта формула больше всего подходит для моделирования процесса распространения вредных примесей выхлопных газов автомобилей в атмосфере, с помощью программного пакета MATLAB R2009b. Путем моделирования процесса распространения вредных примесей в атмосфере, можно проследить взаимосвязи между компонентами данного процесса, это необходимо для установления закономерностей влияния на концентрацию в атмосфере вредных веществ, при выбросе [6].
Выводы
При решении поставленной задачи был выделен подход, который позволит получить пространственное поле концентраций при любых термодинамических состояниях атмосферы и скоростях ветра.
Разработанная модель сочетает в себе различные подходы по исследованию распространений вредных примесей выхлопных газов автомобилей в атмосфере. Её преимущество в том, что она легка для программирования в математических прикладных пакетах, таких как MATLAB, Maple, и других. Единственным минусом модели является то, что она дает результаты только при полном отсутствии ветра (штиле). Вышеуказанные факторы позволяют обеспечить население и экологические службы, отдельно взятого города, о состоянии загрязнения в результате выбросов автомобильного транспорта в атмосферу.
Список использованной литературы
1. Берлянд М.Е. Современные проблемы атмосферной диффузии загрязнения атмосферы. – Л.: Гидрометеоиздат, 1975. – 448 с.
2. Степаненко С.Н., Волошин В.Г., Типцов С.В. Решение уравнения турбулентной диффузии для стационарного точечного источника. – О.: Украинский гидрометеорологический журнал № 3, 2008. – 24 с.
3. Бызова Н.Л., Гаргер Е.Г., Иванов В.Н., Экспериментальные исследования атмосферной диффузии и расчеты рассеяния примесей. – Л.: Гидрометеоиздат, 1991. – 273 с.
4. Семенчин Е.А., Кузякина М.В. Стохастические методы решения обратных задач в математической модели атмосферной диффузии– М.: Физматлит, 2012. – 176 с.
5. Бабков В.С., Ткаченко Т.Ю. Анализ математических моделей распространения примесей от точечных источников. – Д.: Наукові праці ДонНТУ. Серія «Інформатика, кібернетика та обчислювальна техника» № 13, 2011. – 9 с.
6. Марчук Г.И. Математическое моделирование в проблеме окружающей среды. – М.: Наука, 1982. – 320 с.