РЕЗЮМЕ
Практически все потоки, с которыми сталкивается инженер в естественной или антропогенной среде являются турбулентными, что приводит к быстрому смешиванию загрязняющих веществ, введенных в них. Несмотря на многие годы интенсивных исследований в турбулентной диффузии, способности ученых прогнозировать средние загрязняющие распределения являются весьма сомнительными, также как и способность прогнозировать статистические вариации концентраций. В этой главе рассматриваются основные идеи турбулентности и механизмы, с помощью которых скалярные величины, такие, как загрязнители, смешиваются. Также осуществляется попытка вывода эволюционных уравнений для скалярных величин, обсуждаются инженерные допущения, используемые, для того, чтобы сделать скалярные величины податливыми. В статье представлены типовые решения, также даны приложения к различным ситуациям, которые интересуют инженеров, включая коэффициенты диффузии в реках, устьях и прибрежных водах. Сложности процесса диффузии продемонстрированы с использованием новых оптических экспериментальных методик. Также в статье обсуждаются новые методы моделирования, и осуществляется постановка научно-исследовательских вопросов.
1. ВВЕДЕНИЕ
Турбулентная диффузия очень эффективна при уменьшении концентрации загрязняющих веществ, которые выбрасываются в окружающую среду. Несмотря на интенсивные исследования, в течении многих лет, ученые могут делать только приблизительные прогнозы содержания этих концентраций. Большинство математических моделей турбулентной диффузии, в частности инженерных, могут спрогнозировать только усредненные, по времени, концентрации. Хотя часто, и этого может быть достаточно, например, стандарты качества воды, как правило, записаны в усредненных, по времени, значениях, и только иногда может возникать необходимость в знании более подробной информации о статистической вариации флуктуаций концентрации. Это может быть ситуация, когда необходимо спрогнозировать пиковые экспозиции человека относительно загрязнителей воздуха, водных организмов относительно загрязнителей воды, вероятности сгорания горючих газов, случайно выпущенных в атмосферу, или информации, доступной для организма, который пытается определить источник химического запаха, по его шлейфу, через турбулентность. Рассмотрим фотографию пассивной примеси, которая находится в турбулентном потоке, представленную на рис.1. Этот снимок был получен при исследовании химических шлейфов запаха. Даже беглый осмотр этого изображения показывает, что поиск решения, с помощью усредненной концентрации, в любой момент времени, было бы не лучшим выбором для расчета сигналов загрязнений. Этот сигнал состоит из небольшого среднего значения с периодическими колебаниями, которые варьируются от нуля до уровня, порядков выше, чем средний. Нынешние математические модели, как правило, не могут прогнозировать сигналы на более высоких уровнях, с учетом переменчивости пиковых значений функции плотности вероятности, и пространственных корреляций.

Рисунок 1. Химический шлейф реализован изокинетически, в турбулентности потока открытого канала. Соотношение высоты составляет 1/4 глубины канала.
Новые экспериментальные методы позволяют по-новому взглянуть на эти вопросы. К ним относятся не интрузивные оптические методы, в частности метод плоской лазерно-индуцированной флуоресценции (PLIF), для измерения уровней трассирующих концентраций, и метод изображения скорости частиц (PIV), позволяющий измерять скорость. Они позволяют измерять целые области концентраций примеси и скорости, для которых могут быть получены подробные статистические измерения их пространственной изменчивости и корреляции. В данной главе будут использоваться некоторые из методов, для того, чтобы проиллюстрировать сложность турбулентной диффузии.
Целью этой главы является предоставление вводного обзора основных механизмов турбулентной диффузии, некоторых методов прогнозирования средних распределений концентраций, для нескольких избранных приложений, представляющих интерес для инженеров. Будет рассмотрен только случай турбулентной диффузии, то есть распространение скалярной величины из-за нерегулярных турбулентных пульсаций скорости. Это исключает перемешивание, за счет совместного действия диффузии, а также сдвига в средней скорости, которую иногда называют дисперсией сдвига потока. Также, при рассмотрении данной задачи, будет исключен эффект плавучести, из-за разности плотностей сбрасываемых жидкости и принимающей жидкости, и подавления турбулентности из-за стратификации плотности. Вначале дается обзор турбулентных течений, в частности тех особенностей, которые важны для турбулентной диффузии. Затем обсуждаются механизмы, посредством которых турбулентность вызывает быстрое перемешивание, выводятся усредненные по времени уравнения сохранения видов, и нынешние методы оценки полученных турбулентных коэффициентов диффузии. Затем приводятся примеры применения, представляющие интерес для инженеров и биологов. В заключении приведены обсуждения некоторых из новых методов турбулентного моделирования диффузии и определены некоторые новые вопросы исследования.
2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ
Первым шагом в понимании турбулентной диффузии и средних концентраций является понимание, непосредственно, некоторых основных характеристик турбулентности.
2.1 Природа турбулентности
Турбулентность трудно определить точно, тем не менее, есть несколько важных характеристик, которыми обладают все турбулентные потоки. Эти характеристики включают непредсказуемость, скорость диффузии, высокий уровень флуктуации вихря, и рассеивание кинетической энергии.
Скорость движения точки в турбулентном потоке представляется наблюдателю «случайной» или «хаотической». Скорость движения непредсказуема в том смысле, что знания мгновенной скорости в определенный момент времени недостаточно для прогнозирования скорости через некоторое время. Типичная запись скорости представлена на рисунке 2.
Непредсказуемый характер турбулентности требует, чтобы мы описывали движение с помощью статистических мер. Скорость обычно описывается как усредненное по времени значение, плюс некоторое колебание. Средне-временные величины обозначаются верхней чертой.
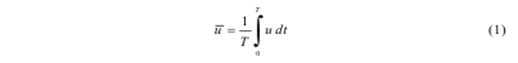
где Т – значения времени, которое гораздо больше самых длинных турбулентных флуктуаций в потоке. Время записи, как показано на рисунке 2 называется статистически стационарным, если средние величины остаются постоянными в течении интересующего нас периода.

Рисунок 2. Образец записи турбулентной скорости.
Для стационарной записи скорости, мгновенную скорость можно разложить в сумму усредненных по времени и колеблющийся взносов (называемых разложением Рейнольдса):
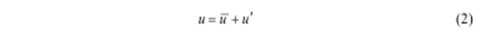
Где u штрих является колеблющимся компонентом (то есть, отклонение от среднего значения), как показано на рисунке 2. По определению, средне-временные колебания равны нулю. Статистические величины высшего порядка, такие как дисперсии, используются для описания величины флуктуации:
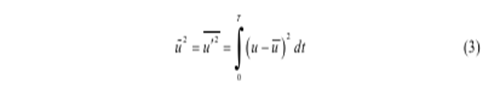
Квадратный корень из дисперсии флуктуации скорости (стандартное отклонение) обозначается u с волной и определяется как интенсивность турбулентности.
Фактически записи скорости, полученные на двух уровнях, в открытом течении в канале, взяты из рисунка 1, и показаны на рисунке 3. Расстояние от стенки обозначено z, а глубина воды d. Усредненная по времени скорость тем больше, чем дальше от стены, как и следовало ожидать в пограничном слое. Интенсивность турбулентности также изменяется с расстоянием от стены, будучи значительно больше вблизи стенки. Изменение средней по времени скорости и интенсивности турбулентности, с расстоянием от нижней планки, показаны на рисунке 4. Средняя скорость возрастает монотонно от нуля вблизи планки; интенсивность турбулентности быстро возрастает от нуля на планке до локального максимума вблизи планки, а затем монотонно уменьшается.
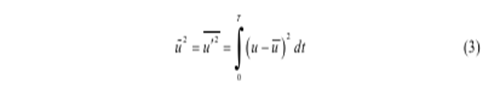
Рисунок 3. Скорость временных каналов, полученных в турбулентном потоке, в открытом канале равна z/d=0.03 (нижний предел), и z/d=0.72 (верхний предел)
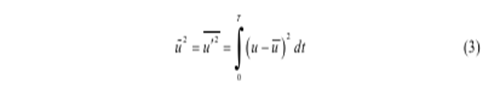
Рисунок 4. (а) усредненное по времени значение и (b) интенсивность для турбулентного потока в открытом канале
Литература
1. Almquist, C.W., and Holley, E.R.(1985). “Transverse Mixing in Meandering Laboratory Channels with Rectangular and Naturally Varying Cross Sections.” Report 205, Center for Research in Water Resources, Univ. of Texas at Austin, Austin, Texas.
2. Chin, D.A., and Roberts, P.J.W. (1985). “Model of Dispersion in Coastal Waters.” Journal of Hydraulic Engineering, ASCE, 111(1), 12-28.
3. Dimou, K.N., and Adams, E.E. (1994). “A Random-Walk, Particle Tracking Model for Well-mixed Estuaries and Coastal Waters.” Est., Coastal and Shelf Sc., 37, 99-110.
4. Hanna, S.R. and Insley, E.M. (1989). “Time Series Analysis of Concentration and Wind Fluctuations.” Boundary-Layer Meteorology, 47, 131-147.
5. Pasquill, F., and Smith, F.B. (1983). “Atmospheric diffusion,” E. Horwood, New York.
6. Roberts, P.J.W. (1996). “Sea Outfalls.” in “Environmental Hydraulics,” V. P. Singh and W. Hager, Editors, Kluwer Academic Publishers, Dordrecht.
7. Smith, R. (1981). “Effect of Non-Uniform Currents and Depth Variations upon Steady Discharges in Shallow Water.” J. Fluid Mech., 110, 373.
8. Taylor, G.I. (1921). “Diffusion by Continuous Movements.” Proc. London Math. Soc., 2(20), 196.
9. Webster, D.R., Roberts, P.J.W., and Ra’ad, L. (2001). “Simultaneous DPTV/PLIF Measurements of a Turbulent Jet.” Experiments in Fluids, 30(1), 65-72.
10. Yotsukura, N., and Sayre, W.W. (1976). “Transverse Mixing in Natural Channels.” Water Resour. Res., 12(4), 695-704.