Аннотация
Кошель А.С., Савкова Е.О. Разработка математической модели плана модернизации медицинского учреждения. Рассмотрена проблема модернизации медицинских учреждений. Приведено описание и обоснование актуальности данной темы. Разработана математическая модель. Изучены и выделены основные методы, используемые для решения подобных задач, проанализированы их достоинства и недостатки.
Ключевые слова: модернизация, медицинское учреждение, оборудование, система поддержки принятия решений, муравьиный алгоритм, граф решений.
Постановка проблемы
Здравоохранение является одной из основных сфер, определяющих качество жизни людей и социальное самочувствие общества. В деятельности любого медучреждения однажды наступает момент, когда обновление медицинского оборудования становится жизненно важной необходимостью. Известно, что в ходе эксплуатации оборудование теряет свои качества. Кроме того, технический прогресс, который не стоит на месте, способствует относительно быстрому моральному устареванию первоначальных эксплуатационных характеристик оборудования. С целью доведения его до уровня, соответствующего современным требованиям к объектам основных средств, учреждения проводят модернизацию.
Использование в медицине устаревших технологий, несвоевременная замена инвентаря приводит к частым поломкам аппаратуры, возникновению форсмажорных ситуаций и высокому риску для людей, проходящих лечение в больницах. Модернизация медицинского оборудования – это залог эффективной помощи пациентам. При выборе масштабов и направления модернизации целесообразно принимать во внимание финансовые ресурсы, возможности практикующих специалистов, т.е. насколько врачи обучены работе с новыми видами оборудования, имеется ли необходимое помещение для установки оборудования. Ведь проблема морального старения зданий больниц и необходимость их соответствующей модернизации как социально значимых объектов является также весьма актуальной. Возникает необходимость подобрать оптимальный вариант обновления медтехники с учётом наличия помещения для оборудования и квалификации медперсонала с минимальными затратами на модернизацию. Поэтому наиболее важным помощником руководителя становятся системы поддержки принятия решений, которые позволяют моделировать ситуацию и сформировать наилучшую стратегию действий.
В некоторых случаях при принятии решений мы допускаем ошибки, имеющие последствия различной степени значимости. Поэтому одним, из несомненных условий успешной деятельности независимо от характера и специфики труда является искусство принятия правильных решений [4].
Цель статьи
Разработать математическую модель плана модернизации медицинского учреждения, провести обзор существующих методов решения данной задачи и выбрать наиболее оптимальный.
Разработка математической модели
Задача построения плана модернизации медицинского учреждения может быть сформулирована как поиск оптимального пути в пространстве принятия решений. Главной задачей является нахождение минимума функционала F при заданных ограничениях. Необходимо найти такое решение, при котором бы выполнялись все ограничения и затраты были минимальные. Пространство принятия решения в общем случае может быть представлено в виде взвешенного графа на рис.1.
Введём понятие взвешенного графа решений. Взвешенный граф решений (G) – граф, каждому ребру которого поставлен в соответствие вес ребра. Такой граф можно представить в виде:
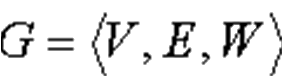 |
(1) |
где
V – множество вершин (действий),
E – множество дуг (рёбер)
W – множество весов.
Дуги могут быть представлены как:
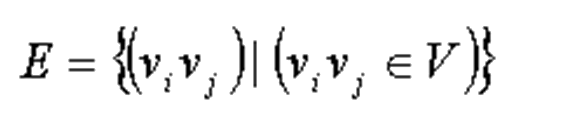 |
(2) |
Дуга соединяет две вершины графа. В качестве вершин графа выступают действия vi vj, которые будут выполняться над объектами модернизации: оборудованием, помещением, персоналом.
Для определения кратчайшего пути из одной вершины в другую необходимо иметь возможность измерять расстояние между узлами (действиями), поэтому введём функцию расстояния, определённую на дугах графа d: E→R, где R – множество вещественых чисел.
Веса учитывают степени рисков, уровни затрат и могут быть представлены в виде:
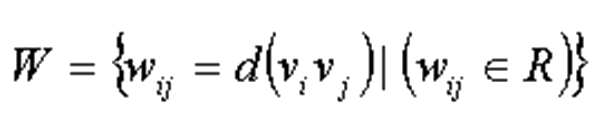 |
(3) |
где wij – вес дуги.
Кроме того введём функции-ограничения для каждого узла. Ограничение – функция, заданная на вершине графа.
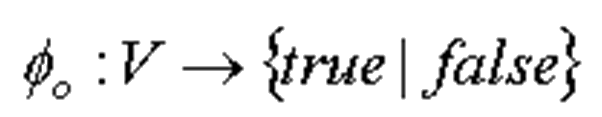 |
(4) |
Ограничения:
- Ограничение на доступный бюджет
- Ограничение на время выполнения
- Ограничения на постройку новых зданий за счет окружающей застройки.
- Имеющиеся обязательства.
- Лимиты по внешним ресурсам (электричество, тепло, вода).
 |
(5) |
 |
(6) |
Необходимо учитывать следующие риски:
- Нарушение сроков строительства.
- Изменение цен на оборудование или материалы, вследствие чего за счет повышения стоимости модернизации возможно нарушение ограничения на доступный бюджет.
Критерий необходимости модернизации
Каждой вершине графа будем сопоставлять индекс в промежутке от 0 до 1. Индекс износа — функция, зависящая от времени. Чем больше индекс, тем больше необходимость модернизации.
Решение поставленной задачи производится в два этапа:
- Просмотр всех имеющихся индексов износа. Все узлы у которых индекс износа больше некоторого заданного порога пометить как требующий модернизации.
- Поиск оптимального решения в пространстве состояний.
Минимум функционала F достигается последовательности вершин, сумма весов которых даёт минимально возможный вес.
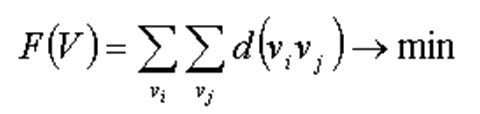 |
(7) |
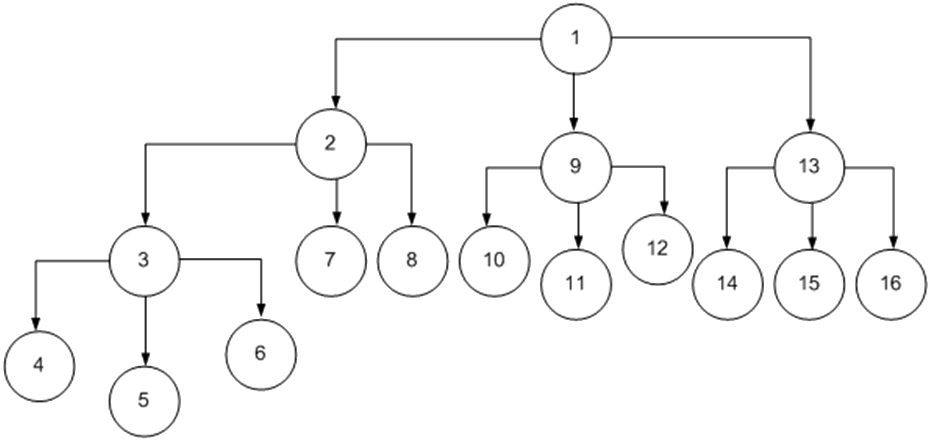
Действиями на графе являются:
- Модернизация
- Выбор оборудования
- Покупка нового
- Наладка
- Монтаж
- Другие расходы
- Ремонт старого
- Не делать ничего
- Выбор помещения
- Строительство нового
- Ремонт старого
- Не делать ничего
- Выбор персонала
- Обучение
- Нанять нового
- Не обучать
Решения
Для решения поставленной задачи подходят следующие алгоритмы:
- Муравьиный алгоритм
- Алгоритм имитации отжига
- Двоичные деревья поиска
- Динамическое программирование
- Алгоритм А* и его модификации
- Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение СПб. БХВ-Петербург, 2003. – 1104 c.
- Russel S., Norvig P. / Рассел С., Норвиг П. – Artificial Intelligence. A Modern Approach, Second Edition / Искусственный интеллект. Современный подход (2-е издание),2006. – 1408 с.
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ, 3-е издание – М.:
Вильямс
, 2013. – 1328 с. - Терелянский П.В. Системы поддержки принятия решений. Опыт проектирования: монография / П. В. Терелянский; ВолгГТУ. – Волгоград, 2009. – 127 c.
- Скобцов Ю.А. Основы эволюционных вычислений. – Донецк: ДонНТУ, 2008. – 326 с.
Муравьиный алгоритм – алгоритм оптимизации подражанием муравьиной колонии, один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра, а также аналогичных задач поиска маршрутов на графах. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую оптимизацию [5].
Муравьиные алгоритмы работают лучше, чем другие глобальные оптимизации (нейронные сети, генетические алгоритмы). Недостатками является то, что обычно необходимо применение дополнительных методов таких, как локальный поиск; сходимость гарантируется, но время сходимости не определено; сильно заисят от настроечных параметров, которые подбираются только исходя из экспериментов. При решении поставленной задачи как субоптимальный метод выбран именно этот алгоритм.
Алгоритм имитации отжига относится к классу пороговых алгоритмов локального поиска. Целью алгоритма является минимизация некоторого функционала. В процессе работы алгоритма хранится текущее решение, которое является промежуточным результатом. А после работы алгоритма оно и будет ответом.
Преимуществами метода являются отсутствие ограничений на вид функции; эффективность при решении задач различных классов, требующих оптимизации, поиск глобального минимума. Недостатками являются сложность настройки алгоритма и его медленная работа [2].
Двоичным деревом поиска называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков, и все вершины, кроме корня, имеют родителя. Вершины, не имеющие потомков, называются листами. Преимуществами являются: лёгкость добавления элемента, лёгкость удаления элемента, быстрый поиск [2].
Одним из недостатков бинарных деревьев является то, что после нескольких операций добавления/удаления элементов такие деревья могут начать вырождаться, что существенно замедлит работу с бинарным деревом.
Метод динамического программирования – один из наиболее мощных и широко известных математических методов современной теории управления, был предложен в конце 50-х годов американским математиком Р. Беллманом.
Динамическое программирование – способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой. Задача имеет оптимальную подструктуру, если её оптимальное решение может быть рационально составлено из оптимальных решений её подзадач.
Кроме принципа оптимальности, основного приема исследования, большую роль в аппарате динамического программирования играет идея погружения конкретной задачи оптимизации в семейство аналогичных задач. Третьей его особенностью, выделяющей его среди других методов оптимизации, является форма конечного результата. Применение принципа оптимальности и принципа погружения в многошаговых, дискретных процессах приводят к рекуррентно-функцио-нальным уравнениям относительно оптимального значения критерия качества. Полученные уравнения позволяют последовательно выписать оптимальные управления для исходной задачи. Выигрыш здесь состоит в том, что задача вычисления управления для всего процесса разбивается на ряд более простых задач вычисления управления для отдельных этапов процесса. Главным недостатком метода является, говоря словами Беллмана, «проклятие размерности» – его сложность катастрофически возрастает с увеличением размерности задачи.
Этот алгоритм был впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Это по сути было расширение алгоритма Дейкстры, созданного в 1959 году. Новый алгоритм достигал более высокой производительности (по времени) с помощью эвристики. В их работе он упоминается как «алгоритм A». Но так как он вычисляет лучший маршрут для заданной эвристики, он был назван A*.
Поиск А* – алгоритм поиска по первому наилучшему совпадению на графе, который находит маршрут с наименьшей стоимостью от одной вершины к другой. Алгоритм работает с «оптимистичной» оценкой пути через вершину. Оптимистичной в том смысле, что, если он пойдёт через эту вершину, у алгоритма «есть шанс», что реальная стоимость результата будет равна этой оценке, но никак не меньше. Алгоритм А* никогда не упустит возможности минимизировать длину пути, и потому является допустимым. Большую проблему представляют собой потребляемые алгоритмом ресурсы памяти.
Выводы
В ходе проведённой работы была разработана математическая модель плана модернизации медицинского учреждения, был проведён обзор существующих методов решения. Рассмотрев основные их достоинства и недостатки, для решения поставленной задачи предполагается выбрать в качестве оптимального метода решения – алгоритм А*, в качестве субоптимального – муравьиный алгоритм.