Аннотация
Лапко В.В., Чередникова О.Ю. Математическая модель переходных аэродинамических процессов в вентиляционных сетях с сосредоточенными и распределенными параметрам. Разработан алгоритм построения математической модели переходных аэродинамических процессов в вентиляционных сетях с сосредоточенными и распределенными параметрами, отличающийся тем, что создание модели исследуемого процесса сводится к обычной коммутации в соответствии с топологией базовых динамических решающих блоков (узлов, ветвей и источников тяги), что обеспечивает наглядный и удобный интерфейс для пользователя при использовании современных программных приложений визуального программирования. Компьютерное моделирование динамической задачи сводится к запуску процедуры одновременного интегрирования дифференциальных уравнений структурных блоков, составляющих сеть.
Введение
Расчету вентиляционных сетей посвящено очень большое количество работ. Однако, большинство работ ориентировано на моделирование и оптимизацию процессов воздухораспределения в сети в стационарном режиме. Моделирование переходных аэродинамических процессов в вентиляционных сетях было выполнено для узкого круга сетей, в которых для описания аэродинамики ветвей достаточно учитывать только акустическую массу воздуха в ветви и сжимаемостью воздушного потока (акустической гибкостью) можно пренебречь. В настоящее время, однако, доказано, что в реальном диапазоне частотного спектра производственных возмущений в шахтных сетях (ω≤0.5 рад/сек) в модели ветвей сети необходимо учитывать сжимаемость воздушного потока, особенно в длинных ветвях, в которых, кроме того, зачастую приходится учитывать и распределенность акустических параметров. Структурная схема модели ветви и сети в целом в этом случае сводится к совокупности однотипных четырехполюсников, объединенных в соответствии с топологией узлами сети. Известны физические и динамические модели сети метрополитена, построенные из совокупности четырехполюсников, на которой были получены важные данные о динамике воздушного потока при движении поездов метрополитена и отработаны оптимальные параметры системы автоматического управления расходом воздуха. Актуальной задачей является создание программной модели такого рода для моделирования широкого спектра динамических возмущений и характеристик ветвей сети.
Математические модели элементов шахтной вентиляционной сети
Основными элементам шахтной вентиляционной сети (ШВС) являются выработки: вентиляционный, откаточный штреки, лава, подготовительные и тупиковые выработки. При моделировании ШВС представляется ориентированным графом, состоящим из ветвей (выработок) и узлов (мест коммутации выработок друг с другом).
В общем случае математическая модель выработки представляет собой систему с распределенными параметрами. Но для упрощения модели с достаточной для практики точностью возможно использовать цепочечные схемы с сосредоточенными параметрами, в которых каждый элемент цепи – четырехполюсник, математическая модель которого представляет собой простые дифференциальные уравнения. Показано, что для обеспечения минимальной сложности модели с достаточной для практики точностью одним четырехполюсником отображается участок выработки длиною до 400м. Экспериментально доказано, что выбор типа четырехполюсника не оказывает существенного влияния на точность модели и выбирается только из условия удобства его коммутации с другими элементами цепи. Наиболее простая схема – схема Г-четырехполюсника показана на рис.1. В схеме замещения учитывается инерционность воздушного потока (L), сжимаемость воздуха (C) и сопротивление выработки(R).

Рисунок 1 – Электрогидравлическая схема замещения отрезка выработки Г-четырехполюсником, учитывающим инерционность, сжимаемость и аэродинамическое сопротивление отрезка выработки
Математическая модель для одного Г-четырехполюсника (рис.1) определяется соотношениями:
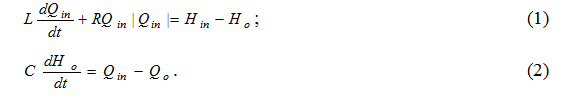
Для удобства построения схемы моделирования представим уравнения (1), (2) в виде:
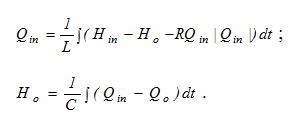
Тогда схема решающего блока, реализующего математическую модель четырехполюсника, и его условное обозначение будут иметь вид, показанный на рис.2.
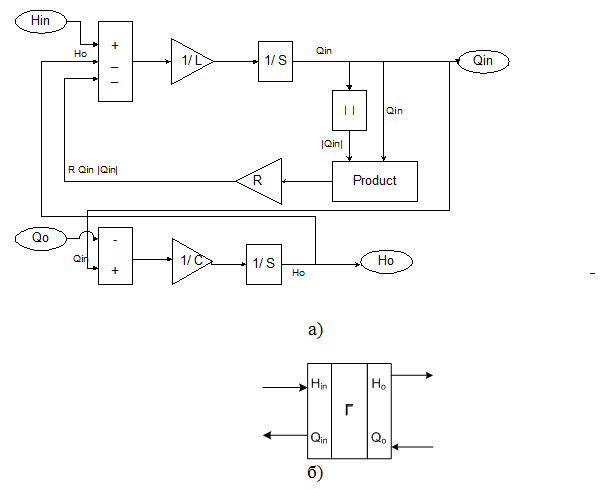
Рисунок 2 – Схема решающих элементов одного Г-четырехполюсника (а) и интерфейс блока по входу и выходу (б)
Входными параметрами блока являются напор на входе цепочечного участка (Нi) и расход воздуха в нагрузке блока (Qо). При работе блока формируется напор в нагрузке цепочечного участка (Но) и значение расхода воздуха на входе блока (Qin) (рис.2,б).
В общем случае для моделирования длинных выработок (ветви) используются цепочечные схемы Г-четырехполюсников (рис.3,а). Коммутационная схема на основе двух четырехполюсников показана на рис.3,б.
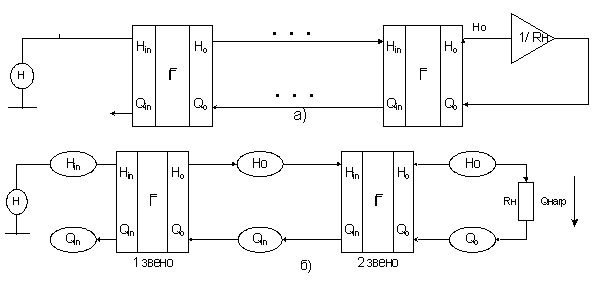
Рисунок 3 – Коммутационная схема ветви на основе двух решающих блоков для Г-образного четырехполюсника
При моделировании узлов ШВС, т.е. мест коммутации выработок друг с другом будем различать разветвляющие узлы (места, где выход одной выработки является началом нескольких выработок (рис.4,б) и суммирующие узлы (места, где выходы нескольких выработок являются входом одной выработки (рис.4,а).
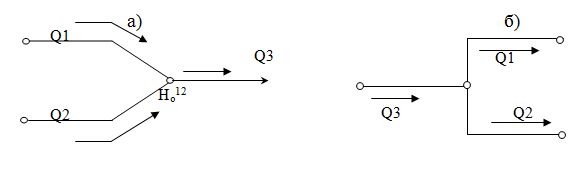
Рисунок 4 – Суммирующий (а) и разветвляющийся (б) узлы
На рис.5 приведена электрогидравлическая схема замещения (а), модель (б) и обозначение блока разветвляющего узла. Входными параметрами этого узла являются входной напор и расходы воздуха на входе двух ветвей, а на выходе блока формируется значение расхода воздуха и значения напоров на входе каждой выработки-ветви.
При моделировании узлов ШВС, т.е. мест коммутации выработок друг с другом будем различать разветвляющие узлы (места, где выход одной выработки является началом нескольких выработок (рис.4,б) и суммирующие узлы (места, где выходы нескольких выработок являются входом одной выработки (рис.4,а).
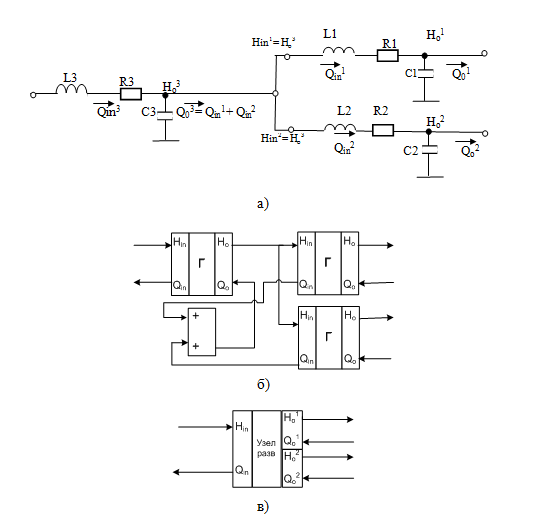
Рисунок 5 – Электрогидравлическая схема замещения (а), коммутационная схема блока (б) и условное обозначение блока (в) разветвляющегося узла
Электрогидравлическая схема замещения суммирующего узла приведена на рис.6. Для удобства моделирования преобразуем эту схему таким образом, как это показано на рис.7.

Рисунок 6 – Электрическая схема суммирующего узла

Рисунок 7 – Эквивалентная схема суммирующего узла
На рис. 8 приведена структура блока суммирующего узла (БСУ) (а) и его обозначение (б). Входными параметрами блока являются входные напоры двух ветвей и расход воздуха на выходе двух ветвей, а на выходе блока выдается начальное значение расходов воздуха для каждой ветви и суммарное значение напора.
Блок «Qc» на рис.8 является общим звеном ветвей 1 и 2. Его математическая модель представлена соотношением:
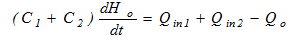
Модель, соответствующая этому описанию приведена на рис.9.
Электрическая схема блока «½ Г» (рис.8) и схема его модели показаны на рис.10. Его математическая модель определяется соотношениями:
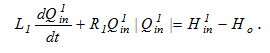

Рисунок 8 – Структура (а) и обозначение (б) блока суммирующего узла

Рисунок 9 – Аналоговая схема собирающего узла
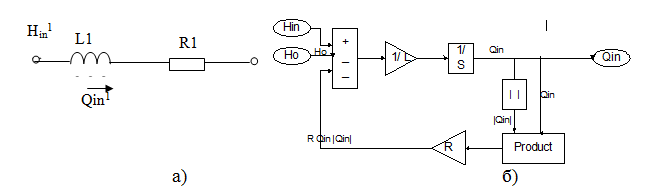
Рисунок 10 – Электрическая (а) и аналоговая схема блока «½ Г»
Заключение
Разработанный алгоритм построения математической модели переходных аэродинамических процессов в вентиляционной сети с сосредоточенными параметрами отличается тем, что создание модели исследуемого процесса сводится к обычной коммутации в соответствии с топологией базовых динамических решающих блоков (узлов, ветвей и источников тяги), что обеспечивает наглядный и удобный интерфейс для пользователя при использовании современных программных приложений визуального программирования. Компьютерное моделирование динамической задачи сводится к запуску процедуры одновременного интегрирования дифференциальных уравнений структурных блоков, составляющих сеть.
В дальнейшем предполагается включение этой модели в систему диспетчерского управления шахтной вентиляционной сетью КАГИ для предварительного имитационного моделирования процессов в ШВС при выборе оптимального управления сетью.
Список использованной литературы
1. Назаренко В.И. Разработка и исследование системы диспетчерского управления проветриванием шахт методами математического моделирования.: Дис. канд. техн. наук. – Донецк, 1974, 222с.
2. Круглов Ю.В. Расчет сложных вентиляционных сетей на ЭВМ / Ю.В. Круглов // Известия вузов. Горный журнал. – 2004. – №2. – С. 46 – 49.
3.Круглов Ю.В. Сравнительный анализ современных алгоритмов расчета вентиляционных сетей / Ю.В. Круглов, А.Г. Исаевич, Л.Ю. Левин // Известия вузов. Горный журнал. – 2006. - №5. – С. 32 – 37.
4. Абрамов Ф.А. Моделирование динамических процессов рудничной аэрологии / Ф.А. Абрамов, Л.П. Фельдман, В.А. Святный. – К.: Наукова думка, 1981. – 284с.
5. Петров Н.Н. Электронная модель системы автоматического управления проветривания шахт.// Н.Н. Петров, П.Н. Ермолаев, П.Т. Пономарев. В кн.: Автоматическое управление в горном деле. Новосибирск: Б.И.,1971, с.89 – 93.