Мультироботное исследование области с использованием метода кругового разбиения.

Аннотация

Upma Jain, Ritu Tiwari, Samriddhi Majumdar, Sanjeev Sharma Мультироботное исследование области с использованием метода кругового разбиения. Исследование неизвестной области является важной темой в мультироботной системе. Благодаря наличию большого количества приложений она вызывает интерес у различных исследователей. В данной работе предлагается подход, основанный на методе кругового разбиения для совместного использования рабочей нагрузки. Неизвестная область разделена на регионы, равные числу доступных роботов, каждый робот отнесен к различным субобластям, а затем команда мобильных роботов начинает исследование. Цель состоит в том, чтобы уменьшить время на исследование. Была использована популярная концепция проблемы исследования, которая основана на понятии границ. Предложенный алгоритм был протестирован в наборе сред с разным уровнем сложности в зависимости от количества препятствий. Этот алгоритм может быть использовано в реальном мире для поисково-спасательных операций, где время – основное ограничение.

1. Введение

Из-за различных преимуществ по сравнению с людьми, роботы предназначены для выполнения сложных задач, таких как исследование во взрывоопасных зонах, разведки и наблюдения, исследования планет [1], поиск и спасение [2], мониторинг окружающей среды и планетарные операции и очистки [3]. В целях обеспечения эффективного исследования многими роботами, необходима надлежащая координация и сотрудничество. Многие подходы, такие как прямая видимость и лидер-последователь [4], граничность и полезность, принцип рынка, теоритический график были предложены для мультироботной разведки области.

С помощью мультироботной системы сравнительно легко достичь скорости, точность, надежность и отказоустойчивость. В мультироботной системе возникает много вопросов, которые влияют на общую производительность системы, такие как координация, взаимодействие, покрытие избыточности, предотвращение столкновений, связь между роботами. В данной работе предлагается подход для мультироботного исследования области неизвестной среды, т.е. на основе метода кругового разбиения.

Остальная часть работы организована следующим образом: раздел II описывает связаные работы. Раздел III описывает постановку задачи. Раздел IV представляет методологию исследования области. Раздел V представляет результат моделирования с использованием Java-апплетов. Завершая статью, в разделе VI излагаются выводы исследования и будущая работа.

2. Связанные работы

Ямаучи, Б. (1997) [5] предложил метод простого исследования, т.е. на основе концепции границ, граница между открытым пространством и неисследованные пространства. Подход рассматривает только одного робота В 1998 Б. Ямочи (1998) [6] расширяет предыдущий подход к исследованию области мультироботами.

В [7] был предложен подход на основе предложения цены за выбор границы. В [8] разработан новый, полностью распределенный алгоритм предлагающий цену, который максимизирует чистую прибыль - взвешенная комбинация, увеличение информации, расстояния перемещения и меры близости. Это снимает проблему информационного несоответствия, вызванного коммуникационной задержкой. В [9] предложена архитектура на основе поведения, предназначенная для руководства роботами децентрализовано с целью изучения окружающей среды и поддержания местной связи малой дальности в мобильной одноранговой сети. В [10] был предложен подход, чтобы минимизировать общее время на разведку, и делает возможным локализовать источник огня в эффективным способом. В [11] алгоритм на основе границы, т.е. на основании новой функции цены предлагается специальный параметр, чтобы уменьшить перекрытие между роботами, вводится в дополнение к полезностных и стоимостных показателей. В [12] предложен распределённый алгоритм, основанный на пограничный карте исследования области, используя модель оптимизации роя частиц для координации робота.

В работе [13] представлен алгоритм координации роботов, который требует алгоритм к-среднего, который разделяет неизвестные пространства на столько областей, сколько доступно роботов. В работе [14], предложен алгоритм на основе разбиения Вороного, был использован для того чтобы разделить неизвестные пространства. В [15] предлагается пространственно распределённый алгоритм, который позволяет команде роботов вычислять выпуклые среды и справедливо разделять выпуклые среды.

В [16] подход, основанный на генетическом алгоритме, был предложен алгоритм планирования пути для местного обхода препятствий мобильным роботом в заданном пространстве поиска. Алгоритм пытается найти действительный, а также оптимальный путь. В [17] был предоставлен подход, основанный на параллельных алгоритмах, эволюционных для кооперативной мультироботной проблемы планирования пути. В [18] был предложен подход с использованием генетических, ANN и A* алгоритмы, которые находят почти самый оптимальный путь для робота. В [19] подход, основанный на MNHS, для планирования пути робота было предложено сделать проблему устойчивой к неопределенностям, которые могут возникнуть, как внезапное обнаружение, в результате путь не приводит к цели. Был предложен в [20] алгоритм оптимального планирования пути, который выбирает кратчайший маршрут с минимальным потреблением энергии. В [21] был предложен алгоритм расширения волнового фронта на основе подхода расширения волны для планирования пути роботов, которые фокусируется на расширении некоторых волн вместо тех, которые пытаются расширить все волны. Это позволяет избежать общего расширения.

K-средних использует итеративный метод вычисления, чтобы вычислить центроиды на различных этапах, таким образом, включающих вычислительную сложность, а также требующих много времени, тогда как метод кругового разделения, упомянутый в статье, уменьшает вычислительное время, в значительной степени, таким образом, делающий этот метод, более благоприятный в ситуациях, где время - важный фактор.

3. Постановка задачи

В этом разделе описывается характер проблемы и предположения, которые были сделаны. Наша цель заключается в изучении окружающей среды с командой мобильных роботов. Стационарные препятствия различной формы и размера размещаются в окружающей среде. Предполагается, что каждый робот имеет возможность локализации, и отображения это означает, что каждый робот способен локализовать себя. Окружающая среда, конечное рабочее пространство, форма и размер рабочей области предопределены. Окружающая среда моделируется как 2D размещенная сетка. При разведке каждая ячейка будет иметь одно из следующих состояний:

1. Неизвестная: заполняемость ячейки, пока не известна.
2. Свободная: ячейка не занята для каких-либо препятствий.
3. Занятая: ячейка занята для каких-либо препятствий

Основная задача – существуют ячейки карты, пересекаемой роботами, по крайней мере, один раз. Робот взят в форме квадрата, его размерность установлена как размер ячейки сетки. Робот использует дальность действия своего датчика, чтобы узнать состояние ячейки.

4. Методология

Предлагаемый нами подход в основном имеет дело с разделением среды для завершения исследования как можно раньше. Первая зона разделена на логические подзоны используя метод кругового разбиения, тогда роботы, назначенные этих логических подзонах начинают разведку в своих логических подрайонах. Чтобы роботы исследовали область нужно двигаться в направлении пограничных клеток. ЕА* алгоритм используется для планирования пути [22].

4.1 Окружающая среда разделов

Среда, которая будет исследоваться, разделена, чтобы разделить целую область на логические подобласти. Из-за подразделения более высокая степень дисперсии достигается среди роботов. Используется подход для разделения среды т.е. на основе метода кругового разбиения. Взяв центр области как центра круга, мы формируем круг, который покрывает, целую область, и затем делит этот круг на число частей равное количеству роботов. С помощью кругового разбиения область разделена на приблизительно равной степени подобласти. Роботы присвоены каждой подобласти в произвольном порядке.

4.2 Покрытие подобластей

Для обеспечения эффективного охвата роботами подобласти должны продолжать двигаться, чтобы пограничные клетки и записи местности соседних ячеек, пока нет граничной клетки, не оставались в той же подобласти. Ячейка, которую в настоящее время занимают роботы, помечается как свободное поле, а значит, была покрыта. В окружающих неисследованных клеток, клетки, занятые препятствиями помечаются как клеточная стенка и клетки, которые не заняты препятствиями, помечаются как граничные клетки. В целях полного изучения подобласти робот двигается к приграничных клеткам на основе алгоритма EA* [22]. Исследование подобласти закончено, когда нет граничной ячейки остававшейся в местной подобласти.

5. Результаты эксперимента

Алгоритм проверяется с использованием Java. Ввод карты задается в виде изображения. Предложенный алгоритм был протестирован с набором сред, указанных на рисунке 1 с разным уровнем сложности в зависимости от количества препятствий. Эксперимент проводили с одинаковыми скоростями для всех роботов.

Рисунок 1 – Моделирование среды (а) Карта-1 с меньшими препятствиями (б) Карта-2 в более сложной сложной среде с большими препятствий

Параметры, используемые в эксперименте, представлены в таблице 1.

Таблица 1 - Параметры используемые в експерименте

Параметр	Значение
Размер карты	100*100
Чувствительность робота	8 ячеек
Количество роботов	4 робота
Инициализация робота	Случайный выбор

Мы сравнили результаты нашего алгоритма с алгоритмом k-средних. Рисунок 2 (а) - (б) показывает карту покрытия, используя круговое разбиение и k-средних для карты 1 соответственно.

Рисунок 2 – (а) Карта покрытия кругового разбиения для Карта 1. (б) охват k-среднего карты для карты 1

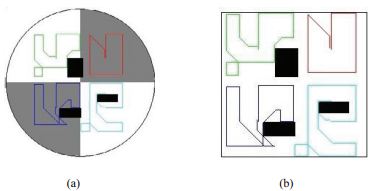
Рисунок 3 (а) - (б) и показывает карту покрытия, используя круг разделов и k-среднее для карты 2 соответственно.

Рисунок 3 – (а) Карта покрытия кругового разбиения для карты 1. (б) охват k-среднего карты для карты 2
Таблица 2 - Сравнение двух методов

Методы разбиения
Карты	Круговоее разбиение	k-средних
Карта 1	6 мин.	8 мин.
Карта 2	9 мин.	10 мин.

Из результатов, следует отметить, что исследование использовании кругового разбиения требует меньше времени по сравнению с алгоритмом k-средних.

6. Выводы

Мы представили новый подход к исследованию области мультироботами; наша главная задача состоит в изучении окружающей среды как можно быстрее. Подход на основе метода кругового раздела для раздела среды представлена в целях максимизовать дисперсию робота в команде мобильных роботов. Предложенный алгоритм был протестирован с набором сред с разным уровнем сложности в зависимости от количества препятствий, моделирования и экспериментальных результатов предложенного метода исследования показывают, что с помощью метода кругового раздела команде мобильных роботов требуется короткий период времени, чтобы завершить исследование. Это объясняется главным образом по той причине, что метод метода создания круговых разделов не требует для вычисления расстояния всех точек из центров тяжести.

Работа может быть продлена в реальных условиях. Мы будем иметь дело с различными формами окружающей среды и рассмотрим ограниченную дальность связи.

Список использованной литературы

1. D. Apostolopouslos et al., “Robotic antarctic meteorite searchioutcomes,” in Proc. IEEE Int. Conf. Robot. Autom. (ICRA), pp. 4174-4179, 2001.
2. J. L. Baxter, E. K. Burke, J. M. Garibaldi and M. Norman, “Multi-Robot Search and Rescue: A Potential Field Based Approach”, IEEE International Conference on Robotics and Automation, Volume 2, Issue, pp 1217-1222, 2002.
3. Rtrdf I. Wagner and A. Bruckstein, “Cooperative cleaners: s study in ant robotics,” Tech. Rep. 9512, CIS Report, Technion, IIT Haifa, June1995.
4. Yintao Wang, “A leader-follower formation control strategy for AUVs based on line-of-sight guidance”, Mechatrons And Automation, ICMA 2009, pp. 4863-4867.
5. B. Yamauchi, “A frontier-based approach for autonomous exploration,” International Symposium on Computational Intelligence in Robotics and Automation, pp. 146-151, 1997.
6. B. Yamauchi, “Frontier-based exploration using multiple robots,” Second International Conference on Autonomous Agents, pp. 47-53, 1998.
7. R. Simmons, D. Apfelbaum, W. Burgard, D. Fox, M. Moors and S.Thrun, and H. Younes, “Coordination for multi-robot exploration and mapping”, in Proceedings of the AAAI National Conference on Artificial Intelligence (AAAI),”2000.
8. Weihua Shenga, Qingyan Yangb, Jindong Tanc and Ning Xid “Distributed multi-robot coordination in area exploration,” Journal of Robotics and Autonomous Systems, Vol.54, Issue 12, 2006R, pp. 945-955
9. J. Vazquez and C. Malcolm, “Distributed multirobot exploration maintaining a mobile network,” International Conference on Intelligent Systems, Vol.3, pp. 113 - 118, 2004.
10. Marjovi, A., Nunes, J.G, Marques, L.,de Almeida, A.,” Multi-Robot Exploration and Fire Searching,” Intelligent Robots and Systems, pp. 1929 - 1934,2009.
11. Al-Khawaldah, S. Livatino and D. Lee, “Frontier based exploration with two Cooperative Mobile Robots,” International Journal of Circuit, Systems and Signal Processing, Vol. 4, Issue 2, 2010.
12. Yiheng Wang, Alei Liang and Haibing Guan,” Frontier-based Multi-Robot Map Exploration Using Particle Swarm Optimization,” IEEE Symposium on Swarm Intelligence (SIS), pp. 1 - 6, 2011.
13. Agusti Solanas and Miguel Angel Garcia,” Coordinated Multi-Robot Exploration Through Unsupervised Clustering of Unknown Space,” International Conference on Intelligent Robots and Systems, Vol.1, pp. 717 - 721, 2004.
14. Ling Wu, Miguel Angel Garcia, Domenec Puig and Albert Sole,” Voronoi-Based Space Partitioning for Coordinated Multi-Robot Exploration”, Journal of Physical Agents, Vol.1, No. 1, Sept. 2007. ISSN 1888-0258, pp.37-44.
15. Marco Pavone, Alessandro Arsie, Emilio Frazzoli, Francesco Bullo,” Distributed Algorithms for Environment Partitioning in Mobile Robotic Networks”, IEEE Transactions On Automatic Control, Vol. 56, Issue 8,pp. 1834 - 1848,2011.
16. K.H. Sedighi, K. Ashenayi, T.W. Manikas, R.L. Wainwright and H. Tai, “Autonomous Local Path Planning for a Mobile Robot Using a Genetic Algorithm,” International Conference on Robotics and Automation, Vol.2, pp. 1338 - 1345, 2004.
17. Jayasree chakraborty, Amit Konar, L.C Jain and Uday K. Chakraborty, “A Distributed Cooperative Multi-Robot Path Planning Using Differential Evolution,” Journal of Intelligent & Fuzzy Systems ,pp. 718 - 725,2008.
18. Kala Rahul :”Mobile Robot Navigation Control in Moving Obstacle Environment using Genetic Algorithm, Artificial Neural Networks and A* Algorithm,” IEEE World Congress on Computer Science and Information Engineering, pp. 705-713 , 2009.
19. Kala Rahul, Shukla Anupam, Tiwari Ritu”Fusion of probabilistic A* algorithm and fuzzy inference system for robotic path planning,” Artificial Intelligence Review Vol.33, pp. 275-306, 2010.
20. Anshika Pal, Ritu Tiwari, and Anupam Shukla,” Multi Robot Exploration using a Modified A* Algorithm,” Third International Conference on Intelligent Information and Database Systems, Vol. 1, pp. 506-516, 2011.
21. Anshika Pal, Ritu Tiwari, and Anupam Shukla,” A Focused Wave Front Algorithm for Mobile Robot Path Planning,” International Conference on Hybrid Artificial Intelligent Systems, Vol. 1, pp. 190-197, 2011.
22. Anshika Pal, Ritu Tiwari, and Anupam Shukla,” Multi Robot Exploration using a Modified A* Algorithm,” Third International Conference on Intelligent Information and Database Systems, Vol. 1, pp. 506-516, 2011.