 Алгоритмы контурной сегментации и распознавания образов объектов систем технического зрения
Алгоритмы контурной сегментации и распознавания образов объектов систем технического зренияАвторы: Нгуен К.М., Колючкин В.Я.
Источник: Нгуен К.М. Алгоритмы контурной сегментации и распознавания образов объектов систем технического зрения / К.М. Нгуен, В.Я. Колючкин // Наука и образование. Электронное научно-технические издание. — Московский автомобильно-дорожный государственный технический университет, 2013. — С. 187–200.
Введение
Разработка и внедрение в промышленность роботизированных комплексов является одним из важнейших направлений в задаче создания систем гибкого автоматизированного производства. Гибкость производства изделий обеспечивается роботизированным комплексом, в состав которого, кроме технологического оборудования и систем управления, входят системы технического зрения (СТЗ), предназначенные для получения информации об изделиях. Например, при выполнении технологических операций на конвейерах СТЗ позволяет осуществлять операции сортировки деталей, определять их положение и ориентацию [1]. При разработке алгоритмов обработки данных в СТЗ сортировка деталей формулируется как задача распознавания образов, регистрируемых аппаратными средствами СТЗ, а определение положения и ориентации – как задача оценки соответствующих параметров изображений этих деталей.
Целью исследований, изложенных в настоящей статье, является разработка алгоритма распознавания образов деталей, которые могут быть использованы в СТЗ роботизированных производственных комплексов. Задачи, решаемые при разработке такого алгоритма, конкретизируются следующими условиями. Во-первых, детали имеют относительно простую форму. Это означает, что контур регистрируемого изображения деталей однозначно характеризует их форму. Во-вторых, распознаванию подлежат детали, которые располагаются на ленте транспортёра открытого конвейера и имеют произвольные ориентации. Поэтому фон, на котором регистрируются изображения деталей, можно считать равномерным, а условия освещения таковы, что тени отсутствуют.
При такой постановке задачи можно использовать алгоритмы распознавания, основанные на анализе контуров регистрируемых изображений деталей. Этот подход позволяет исключить из анализа внутренние точки изображения и тем самым значительно сократить объем обрабатываемой информации за счет перехода от анализа функции двух переменных к функции одной переменной. Известные алгоритмы распознавания, основанные на анализе контуров образов объектов [8, 9, 11], включают следующую последовательность процедур:
- предварительная обработка изображения;
- выделение контуров;
- формирование словаря признаков;
- сопоставление образов с эталонами из базы данных на основе выбранного решающего правила.
Рассмотрим особенности этих процедур для решения поставленной задачи.
Предварительная обработка изображений
Предварительная обработка осуществляется с целью подавления помех, которые возникают в изображении на этапе их регистрации аппаратными средствами или при передаче сигналов по линиям связи. Задачей предварительной обработки является эффективное подавление шума при сохранении важных для последующего распознавания элементов изображения [2, 3]. Для описания шума систем регистрации изображений обычно используют модель белого шума, плотность вероятности которого описывается нормальным законом. Для оценки уровня помех в изображении используют показатель в виде пикового отношения сигнала к шуму, который определяется как μ=LM/σN, где LM — максимальная амплитуда уровня сигнала в изображении, а σN — среднеквадратическое отклонение (СКО) шума.
На этапе предварительной обработки для подавления помех обычно используется фильтр Гаусса [6, 12], параметры которого выбираются на основе анализа пространственно-частотного спектра изображений объектов, подлежащих распознаванию.
Выделение контуров на изображениях
Выделение контуров является одним из методов сегментации изображений [4, 5, 6, 10, 12, 14]. В большинстве методов выделения контуров и основанных на этих методах алгоритмов используются линейные операторы с последующей пороговой обработкой. Некоторые их этих операторов осуществляют вычисление первой производной, как, например, операторы Робертса, Собеля [15, 16], или второй производной (оператор Лапласа [4, 10]). Но эти методы не удовлетворяют требованиям непрерывности и минимальной толщины контурных линий [13]. В обзоре, приведённом в [5], показано, что градиентные методы с простой пороговой обработкой уступают по качеству выделения контуров методу, предложенному Канни [6].
Детектор границ Канни включает следующую последовательность действий. После фильтрации помех на изображении гауссовым фильтром с заданным параметром сглаживания σ в каждой точке изображения вычисляется градиент, который характеризуется значением модуля:
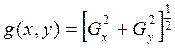
и направлением
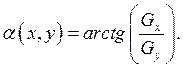
В полученном массиве градиентов производится анализ и отслеживание областей с максимальными градиентами, которые образуют гребни. В процессе этого анализа точкам, не лежащим на гребнях, присваивается нулевое значение. Особенностью этой процедуры является то, что присвоение значения нуля выполняется только в том случае, если значение градиента в этой точке не превышает величины скачка интенсивности в двух соседних точках по одинаковому направлению градиента. В результате выполнения этой процедуры, которая называется немаксимальным подавлением, получается тонкая линия, лежащая на гребне перепадов интенсивности изображения.
Полученное изображение подвергается пороговой обработке с использованием двух порогов T1 и T2, причем T1<T2. Пиксели гребня, значение интенсивности в которых больше T2, называются сильными, а пиксели, значения которых попадают в интервал [T1,T2], называются слабыми. Алгоритм формирования контура завершается морфологической операцией, в процессе которой к сильным пикселям добавляются слабые, которые 8-связаны с сильными пикселями.
Как показано в [12], сглаживание значений интенсивности повышает помехоустойчивость детектора Канни, но снижает точность выделения контуров объектов изображения. Поэтому авторами работы [12] предложено для подчеркивания перепадов интенсивности изображения использовать вейвлет-преобразование, сохраняющее помехоустойчивость методов контурной сегментации изображений, подвергнутых сглаживанию, и в меньшей степени снижающее точность выделения контуров объектов. В качестве показателя помехоустойчивости предложенного метода использовался критерий Прэтта [10], а точность выделения контуров оценивалась показателем близости между границами тестового идеально сегментированного изображения и изображения, сегментированного предложенным методом обработки [17]. Авторами работы [12] показано, что положительный эффект от предложенного вейвлет-преобразования достигается только для частных случаев, когда отношение сигнала к шуму по мощности превышает значение, равное 5, а также при условии, когда ширина перепада границы превышает 3 пикселя. В остальных случаях метод Канни даёт лучшие результаты, по сравнению с предложенным авторами [12] методом контурной сегментации.
Предлагаемый в данной работе метод выделения контуров изображений объектов основан на последовательном применении детектора Канни, а также выполнении ряда морфологических операций обработки изображений, и назван нами комбинированным методом. Суть комбинированного метода иллюстрируется схемой, представленной на рисунке 1.
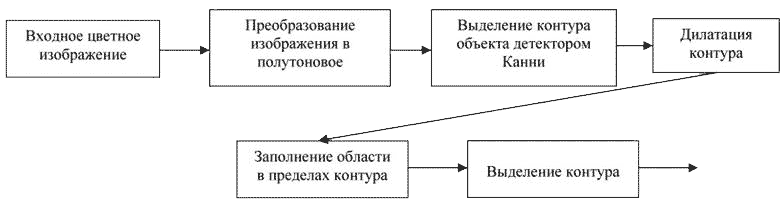
Рисунок 1 — Схема алгоритма контурной сегментации комбинированным методом
Как следует из схемы, комбинированный метод включает процедуру преобразования исходного изображения, в общем случае цветного, в полутоновое изображение, процедуру выделения контура детектором Канни и дополнительные морфологические операции и процедуры, в том числе:
- операцию дилатации бинарного изображения контура, полученного методом Канни;
- процедуру заполнения области внутри контура;
- процедуру выделения контура.
Как известно [4], операция дилатации (наращивания) бинарного изображения, в данном случае границы D, структурообразующим элементом (примитивом) B1 определяется соотношением:
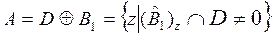
В предлагаемом методе предлагается использовать структурообразующий элемент B1 в виде примитива круглой формы диаметром 5 пикселей.
Процедура заполнения области основана на последовательном выполнении операций дилатации, дополнения и пересечения множеств.В начале процедуры одному из элементов внутри контура присваивается значение, равное 1, после чего производится заполнение всей области единицами в соответствии со следующей рекуррентной формулой [4]:

где: Xk — внутренние элементы в пределах контура, описываемые множеством A; B2 — симметричный примитив в виде креста размерностью 3×3 пикселя; Ac — множество, инверсное множеству A.
Последняя операция процедуры заполнения области — формирование множества C, заключается в объединении множеств Xk и A, а именно, C=Xk∪A.
Процедура β(C) выделения контура множества C, описывающего бинарное изображение, заключается в выполнении операции эрозии C по примитиву B3, а затем получения разностного множества между С и результатом его эрозии [4], т.е. β(C)=C\(CθB3), где B3 — примитив квадратной формы размерностью 3×3 пикселя.
Формирование словаря признаков и выбор классификатора
В данной работе для формирования словаря признаков распознавания объектов по их контурным границам использованы фурье-дескрипторы [4, 7]. На основе фурье-дескрипторов можно сформировать признаки, которые инвариантны к сдвигу, повороту и изменению масштаба границы объекта.
Для вычисления фурье-дескрипторов контур границы объекта представляется в виде массива комплексных чисел ƒ(k)=x{k}+iy(k), k=0,1,2,...,N-1. Выражение дискретного преобразования Фурье для массива ƒ(k) задается выражением [4, 7]:

где u=1,2,3,...,N-1.
Комплексные коэффициенты F(u)=Fu, называются фурье-дескрипторами границы. При формировании вектора признаков используют модули фурье-дескрипторов с положительными и отрицательными индексами u=±1,±2,...,±L/2, причем L≤N-1. Для обеспечения инвариантности признаков к сдвигу, повороту и изменению масштаба выполняют нормировку дескрипторов на модуль дескриптора с индексом u=1. Вектор признаков X представляется в виде:
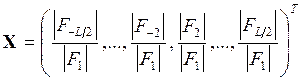
Значение параметра L определяет размерность признакового пространства, которая равна K=L-2.
Для распознавания образов объектов был выбран простейший классификатор, основанный на минимизации евклидова расстояния между вектором Xr признаков распознаваемого объекта ωr и векторами Xm (m=1,...,M) признаков эталонных объектов, образующих алфавит классов [4]. В данном случае количество классов равно M. Евклидово расстояние определяется формулой:
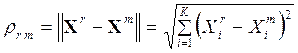
Решение о принадлежности объекта ωr к некоторому классу Ωm* — решающее правило, можно представить соотношением:
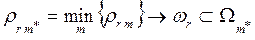
Численные эксперименты
Целью экспериментов являлась сравнительная оценка эффективности алгоритма распознавания образов на основе фурье-дескрипторов контуров объектов, которые получены методом Канни и предложенным комбинированным методом. Для этого в среде MATLAB была разработана программа, в которой реализованы описанные выше алгоритмы выделения контуров и распознавания образов объектов.
Для проведения экспериментов была подготовлена база данных для 40 классов относительно простых объектов, которые регистрировались цифровой камерой. Каждый класс в базе данных включал одно эталонное изображение размером 640х480 пикселей при 256 уровнях квантования. Изображения объектов представлены на равномерном фоне, уровень которого в относительных величинах составлял значение, примерно равное 0,5. Эталонные изображения содержали помеху, обусловленную шумом устройства регистрации со среднеквадратическим отклонением (СКО), которое в относительных единицах оценивалось значением σN=0,0046. Изображения эталонов, образующие базу данных, представлены на рисунке 2.

Рисунок 2 — База данных объектов
Тестовая выборка изображений была подготовлена из эталонных изображений и включала 480 изображений, в том числе: 40 эталонных изображений; 160 изображений, полученных поворотом эталонных изображений на углы 20o, 30o, 60o и 80o; 80 изображений, полученных масштабированием эталонных изображений с коэффициентом масштабирования 0,75 и 0,5; 200 изображений, полученных добавлением к эталонным изображениям аддитивного шума с нормальным законом распределения и СКО, равным 0,036, 0,062, 0,073, 0,086 и 0,101. При проведении экспериментов для распознавания использовалось 98 признаков.
На рисунке 3 приведена иллюстрация выделения контуров объектов по методу Канни и комбинированным методом. В детекторе Канни параметр фильтрации изображения имел значение σ=1,6, значение нижнего порога равнялось T1=0,005, а верхнего — T2=0,02. Из рисунка 3 следует, что визуальное восприятие контуров, полученных комбинированным методом, выше, чем контуров выделенных методом Канни.

Рисунок 3 — Результат выделения контуров объектов а) исходные изображения объектов; б) границы, полученные методом Канни; в) границы, полученные комбинированным методом.
В основной части экспериментов оценивалась эффективность процесса распознавания образов для всех тестовых выборок изображений. Вероятность распознавания изображений оценивалась частотой принятия правильных решений о принадлежности тестовых изображений к определённому классу. Оценка вероятности распознавания, выраженная в процентах, определялась по формуле P=Nr/N0*100%, где Nr — количество положительных исходов при предъявлении тестовых изображений в испытании, а N0 — количество предъявлений тестовых изображений в испытании.
В таблицах 1 и 2 представлены значения вероятности распознавания при предъявлении тестовых изображений, у которых контуры выделялись методом Канни, а также комбинированным методом. В частности, в таблице 2 приведены результаты экспериментов, в которых как тестовые использовались изображения, полученные из эталонных изображений путём изменения масштаба и поворота.
В таблице 2 приведены результаты экспериментов, с тестовыми изображениями, полученными добавлением аддитивного шума с различными значениями СКО.
Таблица 1 — Влияние масштаба и поворота изображения на вероятность распознавания
| Вид тестовой выборки | Вероятность распознавания при выделении контуров методом Канни, % | Вероятность распознавания при выделении контуров комбинированным методом, % |
| Эталонные изображения | 100% | 100 % |
| Коэффициент масштаба изображений 0,75 | 82,5% | 95 % |
| Коэффициент масштаба изображений 0,5 | 50% | 70 % |
| Поворот изображений на угол 20o | 90% | 90% |
| Поворот изображений на угол 30? | 90% | 90% |
| Поворот изображений на угол 60? | 90% | 90% |
| Поворот изображений на угол 80? | 90% | 90% |
Таблица 2 — Влияние значения СКО аддитивного шума на вероятность распознавания
| СКО шума | Вероятность распознавания при выделении контуров методом Канни, % | Вероятность распознавания при выделении контуров комбинированным методом, % |
| 0,036 | 85% | 90% |
| 0,062 | 52,5% | 87.5 % |
| 0,073 | 35% | 85% |
| 0,086 | 32,5% | 80% |
| 0,101 | 25% | 67,5 % |
Из результатов, представленных в таблице 1, следует, что алгоритм распознавания, в котором для выделения границ используется комбинированный метод, является более устойчивым к изменению масштаба изображения. Поворот изображения в одинаковой степени снижает вероятность распознавания, как при выделении границ по методу Канни, так и для комбинированного метода. Как показал анализ, снижение вероятности распознавания при повороте изображения обусловлено искажениями, которые вносит в описание контуров алгоритм поворота изображения.
Из таблицы 2 следует, что увеличение СКО шума в изображении снижает вероятность распознавания для обоих алгоритмом. Но алгоритм распознавания, в котором для выделения границ используется комбинированный метод, является более устойчивым к аддитивному шуму.
Заключение
На основании проведённых исследований можно сделать следующие выводы:
- предложенный комбинированный метод выделения контуров по сравнению с методом Канни обеспечивает более высокую эффективность распознавания образов простых объектов в алгоритмах на основе фурье-дескрипторов;
- предложенный алгоритм распознавания может быть использован в СТЗ роботизированных комплексов при сортировке деталей на открытых конвейерах.
Список использованной литературы
1. Генкин В.Л., Ерош И.Л., Москалев Э.С. Системы распознавания автоматизированных производств. М.: Машиностроение, 1988. — C. 242.
2. Яне Б. Цифровая обработка изображений: пер. с англ. М.: Техносфера, 2007. — C. 584.
3. Грузман И.С., Киричук В.С., Косых В.П., Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в информационных системах: учеб. пособие. Новосибирск: Изд-во НГТУ, 2003. — C. 352.
4. Гонзалес Р., Вудс Р. Цифровая обработка изображений: пер. с англ. М.: Техносфера, 2005. — C. 1072.
5. Стругайло В.В. Обзор методов фильтрации и сегментации цифровых изображений // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 5. DOI: 10.7463/0512.0411847.
6. Canny J. A Computational Approach for Edge Detection // IEEE Trans. Pattern Anal. Machine Intel. 1986. Vol. 8, no. 6. — P. 679–698.
7. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB: пер. с англ. М.: Техносфера, 2006. — C. 616.
8. Granlund G.H. Fourier Pre-processing for Hand Print Character Recognition // IEEE Transactions on Computers. 1972. Vol. C–21. — P. 195–201.
9. Kauppinen H., Seppnen T., Pietikinen M. An Experimental Comparison of Autoregressive and Fourier-Based Descriptors in 2D Shape Classification // IEEE Transactions on Pattern Analysis and Machine Intelligence. Feb. 1995. Vol. 17, no. 2. — P. 201–207.
10. Прэтт У. Цифровая обработка изображений. В 2 кн.: пер. с англ. М.: Мир, 1982. — C. 792.
11. Протасов В.И. Распознавание трёхмерных объектов на сложном фоне по части контура. Режим доступа: http://www.sciteclibrary.ru/rus/catalog/pages/4595.html.
12. Полякова М.В., Крылов В.Н. Морфологический метод контурной сегментации на основе репагулярного вейвлет-преобразования // Труды Одесского политехнического университета. 2006. Вып. 1(25). — С. 98–103.
13. Чочиа П.А. Пирамидальный алгоритм сегментации изображений // Информационные процессы. 2010. Том 10, № 1. С. 23–35. Режим доступа: http://www.jip.ru/2010/23-35-2010.pdf.
14. Clark J.J. Authenticating Edges Produced by Zero-Crossing Algorithms // IEEE Trans. PatternAnalysisMachineIntelligence. 1989. Vol. 12, no. 8. — P. 830–831.
15. Робертс Л. Автоматическое восприятие трехмерных объектов // Интегральные роботы: сб. Вып. 1 / под ред. Г.Е. Поздняка. М.: Мир, 1973. — С. 162–208.
16. Sobel I.E. Camera Models and Machine Perception. Ph.D. Thesis. Palo Alto, Calif., Stanford University, 1970.
17. Абакумов В.Г., Крылов В.Н., Антощук С.Г. Повышение эффективности обработки образной информации в автоматизированных системах // Электроника и связь. 2005. Темат. вып. Проблемы электроники
, ч. 1. — С. 100–105.